Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T00:58:41.925Z Has data issue: false hasContentIssue false
  • English
  • Français

An Extension of the Almost Isolated Singularity of Finite Exponential Order

Published online by Cambridge University Press:  20 January 2009

R. Wilson
R. Wilson
Affiliation:
Department of Mathematics, Bedford College, London
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let f(z) be represented on its circle of convergence |z| = 1 by the Taylor series

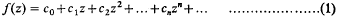
and suppose that its sole singularity on |z| = 1 is an almost isolated singularity at z = 1. In the neighbourhood of such a singularity f(z) is regular on a sufficiently small disk, centre z = 1, with the outward drawn radius along the positive real axis excised. If also in this neighbourhood |f(z)| e−(1/δ)ρ remains bounded for some finite ρ, where δ is the distance from the excised radius, then the singularity is said to be of finite exponential order.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 14 , Issue 2 , December 1964 , pp. 137 - 141
Copyright
Copyright © Edinburgh Mathematical Society 1964

References

REFERENCES

(1)Cartwright, M. L., Proc. London Math. Soc., (2) 38 (1935), 158–179.Google Scholar
(2)Cartwright, M. L., Proc. London Math. Soc., (2) 38 (1935), 503–541.CrossRefGoogle Scholar
(3)Macintyre, A. J. and Wilson, R., Proc. London Math. Soc., (2) 47 (1942), 404–435.CrossRefGoogle Scholar
(4)Macintyre, A. J. and Wilson, R., Jour. London Math. Soc., 16 (1941), 220–229.CrossRefGoogle Scholar
(5)Pólya, G., Annals of Math., (2) 34 (1933), 731–777.CrossRefGoogle Scholar