Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-24T13:27:29.609Z Has data issue: false hasContentIssue false
  • English
  • Français

An aspect of the invariant of degree 4 of the binary quintic

Published online by Cambridge University Press:  20 January 2009

W. L. Edge
W. L. Edge
Affiliation:
Montague House, 67 Mill Hill Musselburgh, EH21 7RLScotland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A binary form of odd degree,

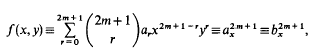
has a quadratic covariant Г, (ab2maxbx in Aronhold's notation, and the discriminant Δ of Г is an invariant of ƒ For m = 2Δ was obtained by Cayley in 1856 [3, p. 274]; it was curiosity as to how Δ could be interpreted geometrically that triggered the writing of this note. An interpretation, in projective space [2m + 1], that does not seem to be on record, of Γ and Δ is found below. If m = 1 one has merely the Hessian and discriminant of a binary cubic whose interpretations in the geometry of the twisted cubic are widely known [5, pp. 241–2].

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 29 , Issue 1 , February 1986 , pp. 133 - 140
Copyright
Copyright © Edinburgh Mathematical Society 1986

References

REFERENCES

1.Baker, H. F., Symbolical algebra and the quadrics containing a rational curve, Proc. Edin. Math. Soc. (1) 44 (1926), 131–143.CrossRefGoogle Scholar
2.Brusotti, L., Sulla curva razionale normale dello spazio a quattro dimensioni, Annali di matematica (3) 9 (1904), 311–352.CrossRefGoogle Scholar
3.Cayley, A., A second memoir on quantics, Phil. Trans. Roy. Soc. 146 (1856), 101–126. Collected Papers II, 250–275.Google Scholar
4.Cayley, A., A third memoir on quantics, Phil. Trans. Roy. Soc. 627–647. Collected Papers II, 310–335.Google Scholar
5.Grace, J. H. and Young, A., The algebra of invariants (Cambridge University Press, 1903).Google Scholar
6.Marletta, G., Sulle curve razionali del quinto ordine, Palermo Rendiconti 19 (1905), 94–119.CrossRefGoogle Scholar
7.Salmon, G., Lessons introductory to the modern higher algebra (Dublin; Hodges, Foster & Co., 1876).Google Scholar
8.Todd, J. A., The geometry of the binary quintic form, Proc. Cambridge Phil. Soc. 40 (1944).CrossRefGoogle Scholar
9.Veronese, G., Behandlung der projektivischen Verhältnisse der Raüme von vershiedenen Dimensionen durch das Prinzip des Projizierens und Schneidens, Math. Annalen 19 (1882), 161–234.CrossRefGoogle Scholar