Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T05:52:58.491Z Has data issue: false hasContentIssue false
  • English
  • Français

An Analogue of the Radon-Nikodym Property for Non-Locally Convex Quasi-Banach Spaces

Published online by Cambridge University Press:  20 January 2009

N. J. Kalton
N. J. Kalton
Affiliation:
Department of Pure Mathematics, University College of Swansea, Singleton Park, Swansea SA2 8PP Department of Mathematics, Michigan State University, East Lansing, Michigan 48824, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In recent years there has been considerable interest in Banach spaces with the Radon-Nikodym Property; see (1) for a summary of the main known results on this class of spaces.We may define this property as follows: a Banach space X has the Radon-Nikodym Property if whenever T ∈ ℒ (L1, X)(where L1 = L1(0, 1)) then T is differentiable i.e.

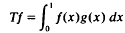
where g:(0, 1)→X is an essentially bounded strongly measurable function. In this paper we examine analogues of the Radon-Nikodym Property for quasi-Banach spaces. If 0>p > 1, there are several possible ways of defining “differentiable” operators on Lp, but they inevitably lead to the conclusion that the only differentiable operator is zero.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 22 , Issue 1 , February 1979 , pp. 49 - 60
Copyright
Copyright © Edinburgh Mathematical Society 1979

References

REFERENCES

(1) Diestel, J., Geometry of Banach spaces - selected topics (Springer Lecture Notes No. 485, Berlin, 1975).CrossRefGoogle Scholar
(2) Edgar, G. A., A non-compact Choquet theorem, Proc. Amer. Math. Soc. 49 (1975), 354–358.CrossRefGoogle Scholar
(3) James, R. C., A nonrefiexive space which is uniformly nonoctrahedral, Israel J. Math. 18 (1974), 145–155.CrossRefGoogle Scholar
(4) Kalton, N. J., Compact and strictly singular operators on Orlicz spaces, Israel J. Math. 26 (1977), 126–136.CrossRefGoogle Scholar
(5) Kalton, N. J., Compact p-convex sets, Quarterly J. Math. (Oxford). 28 (1977), 301–308.CrossRefGoogle Scholar
(6) Kalton, N. J., The endomorphisms of Lp, 0 ≤ p ≤ 1, Indiana Univ. Math J. 27 (1978), 353–381.CrossRefGoogle Scholar
(7) Kalton, N. J., The convexity type of a quasi-Banach space, to appear.Google Scholar
(8) Kalton, N. J. and Peck, N. T., Quotients of Lp(0, 1), 0≤ p < 1, Stadia Math, to appear.Google Scholar
(9) Phelps, R. R., Dentability and extreme points in Banach spaces, J. Functional Analysis 17 (1974), 78–90.CrossRefGoogle Scholar
(10) Pisier, G., Martingales with values in uniformly convex spaces, Israel J. Math. 20 (1975), 325–350.CrossRefGoogle Scholar
(11) Rolewicz, S., Metric Linear Spaces (Warsaw, 1972).Google Scholar
(12) Uhl, J. J., Completely continuous operators on L1 and Liapounoff's theorem (Altgeld Book, 1976).Google Scholar
(13) Fischer, W. and Scholer, U.. On the derivatives of vector measures into lp(x), 0 < p < 1, Comm. Math. 20 (1977) 53–56.Google Scholar