Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T01:10:37.365Z Has data issue: false hasContentIssue false
  • English
  • Français

Alternating units as free factors in the group of units of integral group rings

Part of: Structure and classification of infinite or finite groups Representation theory of groups

Published online by Cambridge University Press:  14 June 2011

Jairo Z. Gonçalves  and
Paula M. Veloso
Jairo Z. Gonçalves
Affiliation:
Departamento de Matemática, Universidade de São Paulo, Rua do Matão 1010, Butantã 05508-090, São Paulo (SP), Brazil ([email protected])
Paula M. Veloso
Affiliation:
Departamento de Matemática, Universidade Federal de Minas Gerais, Av. Antônio Carlos 6627, PO Box 702, 30161-970 Belo Horizonte (MG), Brazil ([email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a group of odd order that contains a non-central element x whose order is either a prime p ≥ 5 or 3l, with l ≥ 2. Then, in 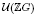, the group of units of ℤG, we can find an alternating unit u based on x, and another unit v, which can be either a bicyclic or an alternating unit, such that for all sufficiently large integers m we have that 〈um, vm〉 = 〈um〉 ∗ 〈vm〉 ≌ ℤ ∗ ℤ

Keywords

integral group ringsfree groupsunits

MSC classification

Secondary: 20C05: Group rings of finite groups and their modules 20E05: Free nonabelian groups
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 54 , Issue 3 , October 2011 , pp. 695 - 709
Copyright
Copyright © Edinburgh Mathematical Society 2011

References

1.Dooms, A., Jespers, E. and Ruiz, M., Free groups and subgroups of finite index in the unit group of an integral group ring, Commun. Alg. 35 (2007), 2879–2888.Google Scholar
2.Ferraz, R. A., Free subgroups in the units of ℤ[K 8 × Cp], Commun. Alg. 31 (2003), 4291–4299.Google Scholar
3.Gonçalves, J. Z. and del Rio, A., Bicyclic units, Bass cyclic units and free groups, J. Group Theory 11 (2008), 247–265.Google Scholar
4.Gonçalves, J. Z. and del Rio, A., Bass cyclic units as factors in a free group, Int. J. Alg. Computat., in press.Google Scholar
5.Gonçalves, J. Z. and Passman, D. S., Embedding free products in the unit group of an integral group ring, Arch. Math. 82 (2004), 97–102.Google Scholar
6.Gonçalves, J. Z. and Passman, D. S., Linear groups and group rings, J. Alg. 295 (2006), 94–118.CrossRefGoogle Scholar
7.Gonçalves, J. Z. and Passman, D. S., Involutions and free pairs of bicyclic units in integral group rings, J. Group Theory 13 (2010), 721–742.CrossRefGoogle Scholar
8.Gonçalves, J. Z. and Veloso, P. M., Special units, unipotent units and free groups in group algebras, Contemporary Mathematics, Volume 499, pp. 127–140 (American Mathematical Society, Providence, RI, 2009).Google Scholar
9.Hall, M., The theory of groups (Macmillan, New York, 1959).Google Scholar
10.Hartley, B. and Pickel, P. F., Free subgroups in the unit groups of integral group rings, Can. J. Math. 32 (1980), 1342–1352.Google Scholar
11.Jespers, E., del Rio, A. and Ruiz, M., Groups generated by two bicyclic units in integral group rings, J. Group Theory 5 (2002), 493–511.Google Scholar
12.Marciniak, Z. S. and Sehgal, S. K., Constructing free subgroups of integral group rings, Proc. Am. Math. Soc. 125 (1997), 1005–1009.CrossRefGoogle Scholar
13.Sehgal, S. K., Units in integral group rings (Longman, New York, 1993).Google Scholar