In the proof of the binomial theorem for negative and fractional indices given in many text-books of algebra, and attributed to Euler, one step seems to me to involve a very gross assumption.

The symbol f(m) having been taken to denote the series

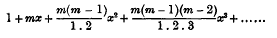
it is pointed out that whenever m and n are positive integers we know that f(x)×f(n)≡f(m + n); and the conclusion is drawn that since this is true for all positive integral values of m and n, by the “permanence of equivalent forms” (whatever that may mean) we can conclude that it is true also for negative and fractional values of m and n, whenever f(m) and f(n) are convergent.