Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T15:04:31.748Z Has data issue: false hasContentIssue false
  • English
  • Français

Two theorems on balanced braces

Part of: Rings and algebras with additional structure Hopf algebras, quantum groups and related topics

Published online by Cambridge University Press:  05 May 2021

Wolfgang Rump
Wolfgang Rump*
Affiliation:
Institute for Algebra and Number Theory, University of Stuttgart, Pfaffenwaldring 57, D-70550Stuttgart, Germany ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Two theorems of Gateva-Ivanova [Set-theoretic solutions of the Yang-Baxter equation, braces and symmetric groups, Adv. Math. 338 (2018), 649–701] on square-free set-theoretic solutions to the Yang–Baxter equation are extended to a wide class of solutions. The square-free hypothesis is almost completely removed. Gateva-Ivanova and Majid's ‘cyclic’ condition ${\boldsymbol {\rm lri}}$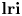 is shown to be equivalent to balancedness, introduced in Rump [A decomposition theorem for square-free unitary solutions of the quantum Yang-Baxter equation, Adv. Math. 193 (2005), 40–55]. Basic results on balanced solutions are established. For example, it is proved that every finite, not necessarily square-free, balanced brace determines a multipermutation solution.

Keywords

Yang–Baxter equationcycle setbracemultipermutation solution

MSC classification

Primary: 16T25: Yang-Baxter equations
Secondary: 16W22: Actions of groups and semigroups; invariant theory
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 2 , May 2021 , pp. 262 - 278
Check for updates
Copyright
Copyright © The Author(s) 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Dedicated to B. V. M.

References

Angiono, I., Galindo, C. and Vendramin, L., Hopf braces and Yang-Baxter operators, Proc. Amer. Math. Soc. 145(5) (2017), 1981–1995.CrossRefGoogle Scholar
Bachiller, D., Classification of braces of order $p^{3}$, J. Pure Appl. Algebra 219(8) (2015), 3568–3603.CrossRefGoogle Scholar
Bachiller, D., Counterexample to a conjecture about braces, J. Algebra 453 (2016), 160–176.CrossRefGoogle Scholar
Cedó, F., Jespers, E. and Okniński, J., Braces and the Yang-Baxter equation, Comm. Math. Phys. 327(1) (2014), 101–116.CrossRefGoogle Scholar
Childs, L. N., Fixed-point free endomorphisms and Hopf Galois structures, Proc. Amer. Math. Soc. 141(4) (2013), 1255–1265.CrossRefGoogle Scholar
Chouraqui, F. and Godelle, E., Finite quotients of groups of I-type, Adv. Math. 258 (2014), 46–68.CrossRefGoogle Scholar
Dehornoy, P., Set-theoretic solutions of the Yang-Baxter equation, RC-calculus, and Garside germs, Adv. Math. 282 (2015), 93–127.CrossRefGoogle Scholar
Drinfeld, V. G., On some unsolved problems in quantum group theory, in Quantum Groups (Leningrad, 1990), Lecture Notes in Mathematics, Volume 1510, pp. 1–8 (Springer-Verlag, Berlin, 1992).CrossRefGoogle Scholar
Etingof, P., Schedler, T. and Soloviev, A., Set-theoretical solutions to the quantum Yang-Baxter equation, Duke Math. J. 100 (1999), 169–209.CrossRefGoogle Scholar
Fenn, R. and Rourke, C., Racks and links in codimension two, J. Knot Theory Ramifications 1(4) (1992), 343–406.CrossRefGoogle Scholar
Gateva-Ivanova, T., Regularity of skew-polynomial rings with binomial relations, in Talk at the International Algebra Conference, Miskolc, Hungary, 1996.CrossRefGoogle Scholar
Gateva-Ivanova, T., Noetherian properties of skew-polynomial rings with binomial relations, Trans. Amer. Math. Soc. 343 (1994), 203–219.CrossRefGoogle Scholar
Gateva-Ivanova, T., Quadratic algebras, Yang-Baxter equation, and Artin-Schelter regularity, Adv. Math. 230(4–6) (2012), 2152–2175.CrossRefGoogle Scholar
Gateva-Ivanova, T., Set-theoretic solutions of the Yang-Baxter equation, braces and symmetric groups, Adv. Math. 338 (2018), 649–701.CrossRefGoogle Scholar
Gateva-Ivanova, T. and Cameron, P., Multipermutation solutions of the Yang-Baxter equation, Comm. Math. Phys. 309(3) (2012), 583–621.CrossRefGoogle Scholar
Gateva-Ivanova, T. and Majid, S., Set-theoretic solutions of the Yang-Baxter equation, graphs and computations, J. Symbolic Comput. 42(11–12) (2007), 1079–1112.CrossRefGoogle Scholar
Gateva-Ivanova, T. and Majid, S., Matched pairs approach to set theoretic solutions of the Yang-Baxter equation, J. Algebra 319(4) (2008), 1462–1529.CrossRefGoogle Scholar
Gateva-Ivanova, T. and Majid, S., Quantum spaces associated to multipermutation solutions of level two, Algebr. Represent. Theory 14(2) (2011), 341–376.CrossRefGoogle Scholar
Gateva-Ivanova, T. and Van den Bergh, M., Semigroups of I-type, J. Algebra 206 (1998), 97–112.CrossRefGoogle Scholar
Helmstetter, J. and Micali, A., About the structure of meson algebras, Adv. Appl. Clifford Algebr. 20(3–4) (2010), 617–629.CrossRefGoogle Scholar
Jedlička, P., Pilitowska, A. and Zamojska-Dzienio, A., The construction of multipermutation solutions of the Yang-Baxter equation of level 2, J. Comb. Theory 176 (2020), 105295.CrossRefGoogle Scholar
Joyal, A. and Street, R., Braided tensor categories, Adv. Math. 102(1) (1993), 20–78.CrossRefGoogle Scholar
Joyce, D., A classifying invariant of knots, the knot quandle, J. Pure Appl. Algebra 23(1) (1982), 37–65.CrossRefGoogle Scholar
Kemmer, N., The algebra of meson matrices, Proc. Cambridge Philos. Soc. 39 (1943), 189–196.CrossRefGoogle Scholar
Lu, J.-H., Yan, M. and Zhu, Y.-C., On the set-theoretical Yang-Baxter equation, Duke Math. J. 104 (2000), 1–18.CrossRefGoogle Scholar
Micali, A. and Rachidi, M., On meson algebras, Adv. Appl. Clifford Algebr. 18(3–4) (2008), 875–889.CrossRefGoogle Scholar
Pilitowska, A. and Romanowska, A., Reductive modes, Period. Math. Hungar. 36(1) (1998), 67–78.CrossRefGoogle Scholar
Rump, W., A decomposition theorem for square-free unitary solutions of the quantum Yang-Baxter equation, Adv. Math. 193 (2005), 40–55.CrossRefGoogle Scholar
Rump, W., Braces, radical rings, and the quantum Yang-Baxter equation, J. Algebra 307(1) (2007), 153–170.CrossRefGoogle Scholar
Rump, W., The brace of a classical group, Note Mat. 34(1) (2014), 115–144.Google Scholar
Rump, W., Right $l$-groups, geometric garside groups, and solutions of the quantum Yang-Baxter equation, J. Algebra 439 (2015), 470–510.CrossRefGoogle Scholar
Rump, W., Classification of cyclic braces, II, Trans. Amer. Math. Soc. 372(1) (2019), 305–328.CrossRefGoogle Scholar
Rump, W., Construction of finite braces, Ann. Comb. 23(2) (2019), 391–416.CrossRefGoogle Scholar
Rump, W., A covering theory for non-involutive set-theoretic solutions to the Yang-Baxter equation, J. Algebra 520 (2019), 136–170.CrossRefGoogle Scholar
Rump, W., One generator braces and indecomposable set-theoretic solutions to the Yang-Baxter equation, Proc. Edinb. Math. Soc 63(3) (2020), 676–696. https://doi.org/610.1017/S0013091520000073.CrossRefGoogle Scholar
Tate, J. and Van den Bergh, M., Homological properties of Sklyanin Algebras, Invent. Math. 124 (1996), 619–647.CrossRefGoogle Scholar
Weinstein, A. and Xu, P., Classical solutions of the quantum Yang-Baxter equation, Comm. Math. Phys. 148(2) (1992), 309–343.CrossRefGoogle Scholar