Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-25T16:18:02.407Z Has data issue: false hasContentIssue false
  • English
  • Français

Tilting pairs in extriangulated categories

Part of: Abelian categories Homological algebra

Published online by Cambridge University Press:  26 October 2021

Tiwei Zhao ,
Bin Zhu  and
Xiao Zhuang
Tiwei Zhao
Affiliation:
School of Mathematical Sciences, Qufu Normal University, Qufu273165, P. R. China ([email protected])
Bin Zhu
Affiliation:
Department of Mathematical Sciences, Tsinghua University, Beijing100084, P. R. China ([email protected])
Xiao Zhuang
Affiliation:
Institute of Mathematics and Physics, Beijing Union University, Beijing100101, P. R. China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Extriangulated categories were introduced by Nakaoka and Palu to give a unification of properties in exact categories and extension-closed subcategories of triangulated categories. A notion of tilting pairs in an extriangulated category is introduced in this paper. We give a Bazzoni characterization of tilting pairs in this setting. We also obtain the Auslander–Reiten correspondence of tilting pairs which classifies finite $\mathcal {C}$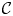-tilting subcategories for a certain self-orthogonal subcategory $\mathcal {C}$ 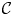with some assumptions. This generalizes the known results given by Wei and Xi for the categories of finitely generated modules over Artin algebras, thereby providing new insights in exact and triangulated categories.

Keywords

extriangulated categorytilting pairBazzoni characterizationAuslander–Reiten correspondence

MSC classification

Primary: 18G10: Resolutions; derived functors 18E10: Exact categories, abelian categories
Secondary: 18G25: Relative homological algebra, projective classes
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 4 , November 2021 , pp. 947 - 981
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aihara, T. and Iyama, O., Silting mutation in triangulated categories, J. Lond. Math. Soc. 85 (2012), 633–668.CrossRefGoogle Scholar
Auslander, M. and Reiten, I., Applications of contravariantly finite subcategories, Adv. Math. 86(1) (1991), 111–152.CrossRefGoogle Scholar
Auslander, M., Platzeck, M. I. and Reiten, I., Coxeter functors without diagrams, Trans. Am. Math. Soc. 250 (1979), 1–46.CrossRefGoogle Scholar
Bazzoni, S., A characterization of $n$-cotilting and $n$-tilting modules, J. Algebra 273(1) (2004), 359–372.CrossRefGoogle Scholar
Bernstein, I. N., Gelfand, I. M. and Ponomarev, V. A., Coxeter functors and Gabriel's Theorem, Uspichi Mat. Nauk. 28 (1973), 19–33. (in Russian), English translation in Russian Math. Surveys 28 (1973), 17–32.Google Scholar
Brenner, S. and Butler, M. C. R., Generalizations of the Bernstein-Gelfand-Ponomarev reflection functors, Representation theory, II, in Proc. Second Internat. Conf., Carleton Univ., Ottawa, Ont., 1979, Lecture Notes in Math., Volume 832, pp. 103–169 (Berlin-New York, Springer, 1980).10.1007/BFb0088461CrossRefGoogle Scholar
Buan, A. B. and Zhou, Y., A silting theorem, J. Pure Appl. Algebra 220 (2016), 2748–2770.CrossRefGoogle Scholar
Chang, W., Zhou, P. and Zhu, B., Cluster subalgebras and cotorsion pairs in Frobenius extriangulated categories, Algebr. Represent. Theor. 22 (2019), 1051–1081.CrossRefGoogle Scholar
Colpi, R. and Trlifaj, J., Tilting modules and tilting torsion theories, J. Algebra 178(2) (1995), 614–634.CrossRefGoogle Scholar
Di, Z., Liu, Z., Wang, J. and Wei, J., An Auslander–Buchweitz approximation approach to (pre)silting subcategories in triangulated categories, J. Algebra 525 (2019), 42–63.CrossRefGoogle Scholar
Happel, D. and Ringel, C. M., Tilted algebras, Trans. Am. Math. Soc. 274(2) (1982), 399–443.CrossRefGoogle Scholar
Iyama, O., Nakaoka, H. and Palu, Y., Auslander–Reiten theory in extriangulated categories, arXiv:1805.03776Google Scholar
Liu, Y. and Nakaoka, H., Hearts of twin cotorsion pairs on extriangulated categories, J. Algebra 528 (2019), 96–149.10.1016/j.jalgebra.2019.03.005CrossRefGoogle Scholar
Miyashita, Y., Tilting modules associated with a series of idempotent ideals, J. Algebra 238(2) (2001), 485–501.10.1006/jabr.2000.8659CrossRefGoogle Scholar
Nakaoka, H. and Palu, Y., External triangulation of the homotopy category of exact quasi-category, arXiv: 2004.02479.Google Scholar
Nakaoka, H. and Palu, Y., Extriangulated categories, Hovey twin cotorsion pairs and model structures, Cah. Topol. Géom. Différ. Catég. 60(2) (2019), 117–193.Google Scholar
Padrol, A., Palu, Y., Pilaud, V. and Plamondon, P.-G., Associahedra for finite type cluster algebras and minimal relations between g-vectors, arXiv: 1906.06861.Google Scholar
Wei, J., Semi-tilting complexes, Israel J. Math. 194 (2013), 871–893.10.1007/s11856-012-0093-1CrossRefGoogle Scholar
Wei, J. and Xi, C., A characterization of the tilting pair, J. Algebra 317(1) (2007), 376–391.CrossRefGoogle Scholar
Wei, J. and Xi, C., Auslander-Reiten correspondence for tilting pairs, J. Pure Appl. Algebra 212(2) (2008), 411–422.CrossRefGoogle Scholar
Zhao, T., Tan, L. and Huang, Z., Almost split triangles and morphisms determined by objects in extriangulated categories, J. Algebra 559 (2020), 346–378.CrossRefGoogle Scholar
Zhou, P. and Zhu, B., Triangulated quotient categories revisited, J. Algebra 502 (2018), 196–232.CrossRefGoogle Scholar
Zhu, B. and Zhuang, X., Tilting subcategories in extriangulated categories, Front. Math. China 15 (2020), 225–253.CrossRefGoogle Scholar