Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-05T16:37:33.450Z Has data issue: false hasContentIssue false
  • English
  • Français

There are no universal ternary quadratic forms over biquadratic fields

Part of: Forms and linear algebraic groups Algebraic number theory: global fields

Published online by Cambridge University Press:  16 September 2020

Jakub Krásenský ,
Magdaléna Tinková  and
Kristýna Zemková
Jakub Krásenský
Affiliation:
Charles University, Faculty of Mathematics and Physics, Department of Algebra, Sokolovská 83, 18600Praha 8, Czech Republic ([email protected]; [email protected])
Magdaléna Tinková
Affiliation:
Charles University, Faculty of Mathematics and Physics, Department of Algebra, Sokolovská 83, 18600Praha 8, Czech Republic ([email protected]; [email protected])
Kristýna Zemková*
Affiliation:
Fakultät für Mathematik, Technische Universität Dortmund, D-44221Dortmund, Germany ([email protected])
*
*Corresponding author.
Get access Rights & Permissions [Opens in a new window]

Abstract

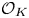We study totally positive definite quadratic forms over the ring of integers $\mathcal {O}_K$ of a totally real biquadratic field 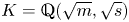$K=\mathbb {Q}(\sqrt {m}, \sqrt {s})$. We restrict our attention to classic forms (i.e. those with all non-diagonal coefficients in 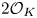$2\mathcal {O}_K$) and prove that no such forms in three variables are universal (i.e. represent all totally positive elements of 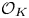$\mathcal {O}_K$). Moreover, we show the same result for totally real number fields containing at least one non-square totally positive unit and satisfying some other mild conditions. These results provide further evidence towards Kitaoka's conjecture that there are only finitely many number fields over which such forms exist. One of our main tools are additively indecomposable elements of 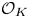$\mathcal {O}_K$; we prove several new results about their properties.

Keywords

Indecomposable integeruniversal quadratic formternary quadratic formbiquadratic number field

MSC classification

Primary: 11E20: General ternary and quaternary quadratic forms; forms of more than two variables
Secondary: 11E12: Quadratic forms over global rings and fields 11R04: Algebraic numbers; rings of algebraic integers 11R80: Totally real fields
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 63 , Issue 3 , August 2020 , pp. 861 - 912
Check for updates
Copyright
Copyright © The Authors, 2020. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bhargava, M. and Hanke, J., Universal quadratic forms and the 290-theorem, Invent. Math., to appear.Google Scholar
Blomer, V. and Kala, V., Number fields without n-ary universal quadratic forms, Math. Proc. Cambridge Philos. Soc. 159(2) (2015), 239–252.CrossRefGoogle Scholar
Blomer, V. and Kala, V., On the rank of universal quadratic forms over real quadratic fields, Doc. Math. 23 (2018), 15–34.Google Scholar
Brunotte, H., Zur Zerlegung totalpositiver Zahlen in Ordnungen totalreeller algebraischer Zahlkörper, Arch. Math. (Basel) 41(6) (1983), 502–503.10.1007/BF01198578CrossRefGoogle Scholar
Chan, W. K., Kim, M.-H. and Raghavan, S., Ternary universal integral quadratic forms over real quadratic fields, Japan. J. Math. 22 (1996), 263–273.CrossRefGoogle Scholar
Čech, M., Lachman, D., Svoboda, J., Tinková, M. and Zemková, K., Universal quadratic forms and indecomposables over biquadratic fields, Math. Nachr. 292 (2019), 540–555. doi:10.1002/mana.201800109CrossRefGoogle Scholar
Deutsch, J. I., Universality of a non-classical integral quadratic form over $\mathbb {Q}[\sqrt 5]$, Acta Arith. 136 (2009), 229–242.CrossRefGoogle Scholar
Dress, A. and Scharlau, R., Indecomposable totally positive numbers in real quadratic orders, J. Num. Theory 14 (1982), 292–306.CrossRefGoogle Scholar
Earnest, A. G. and Khosravani, A., Universal positive quaternary quadratic lattices over totally real number fields, Mathematika 44 (1997), 342–347.CrossRefGoogle Scholar
Jarvis, F., Algebraic Number Theory (Springer, 2007).Google Scholar
Jang, S. W. and Kim, B. M., A refinement of the Dress–Scharlau theorem, J. Number Theory 158 (2016), 234–243.CrossRefGoogle Scholar
Hsia, John S., Kitaoka, Yoshiyuki and Kneser, Martin, Representations of positive definite quadratic forms, J. Reine Angew. Math. 301 (1978), 132–141.Google Scholar
Kala, V., Universal quadratic forms and elements of small norm in real quadratic fields, Bull. Aust. Math. Soc. 94 (2016), 7–14.CrossRefGoogle Scholar
Kala, V., Norms of indecomposable integers in real quadratic fields, J. Number Theory 166 (2016), 193–207.CrossRefGoogle Scholar
Kim, B. M., Finiteness of real quadratic fields which admit positive integral diagonal septenary universal forms, Manuscr. Math. 99 (1999), 181–184.10.1007/s002290050168CrossRefGoogle Scholar
Kim, B. M., Universal octonary diagonal forms over some real quadratic fields, Commentarii Math. Helv. 75 (2000), 410–414.CrossRefGoogle Scholar
Kala, V. and Svoboda, J., Universal quadratic forms over multiquadratic fields, Ramanujan J. 48 (2019), 151–157.CrossRefGoogle Scholar
Maass, H., Über die Darstellung total positiver Zahlen des Körpers $R(\sqrt {5})$ als Summe von drei Quadraten, Abh. Math. Sem. Hamburg 14 (1941), 185–191.CrossRefGoogle Scholar
Milne, J. S., Algebraic Number Theory (v3.07), 2017, Available at www.jmilne.org/math/.Google Scholar
Mazur, M. and Ullom, S. V., Galois module structure of units in real biquadratic number fields, Acta Arithmetica 111(2), (2004), 105–124.CrossRefGoogle Scholar
O'Meara, O. T., Introduction to Quadratic Forms (Springer Verlag, 1973).CrossRefGoogle Scholar
Perron, O., Die Lehre von den Kettenbrüchen (B. G. Teubner, 1913).Google Scholar
Ross, A. E., On representation of integers by quadratic forms, Proc. Nat. Acad. Sci. 18 (1932), 600–608.CrossRefGoogle ScholarPubMed
Sasaki, H., Quaternary universal forms over $\mathbb {Q}[\sqrt 13]$, Ramanujan J. 18 (2009), 73–80.CrossRefGoogle Scholar
Siegel, C. L., Sums of m-th powers of algebraic integers, Ann. Math. 46 (1945), 313–339.CrossRefGoogle Scholar
Ramanujan, S., On the expression of a number in the form ax 2 + by 2 + cz 2 + du 2, Proc. Cambridge Philos. Soc 19 (1917), 11–21.Google Scholar
Tinková, M. and Voutier, P., Indecomposable integers in real quadratic fields, J. Number Theory, 25 pp., to appear.Google Scholar
Williams, K. S., Integers of biquadratic fields, Canad. Math. Bull. 13 (1970), 519–526.CrossRefGoogle Scholar
Yatsyna, P., A lower bound for the rank of a universal quadratic form with integer coefficients in a totally real number field, Comment Math. Helv. 94(2) (2019), 221–239.10.4171/CMH/459CrossRefGoogle Scholar