Hostname: page-component-669899f699-7xsfk Total loading time: 0 Render date: 2025-04-27T06:48:53.578Z Has data issue: false hasContentIssue false
  • English
  • Français

Teichmüller displacement theorem on Gromov hyperbolic spaces

Part of: Analysis on metric spaces

Published online by Cambridge University Press:  06 November 2024

Qingshan Zhou Open the ORCID record for Qingshan Zhou [Opens in a new window] ,
Saminathan Ponnusamy Open the ORCID record for Saminathan Ponnusamy [Opens in a new window]  and
Qianghua Luo Open the ORCID record for Qianghua Luo [Opens in a new window]
Qingshan Zhou
Affiliation:
School of Mathematics, Foshan University, Foshan, Guangdong Province, People’s Republic of China
Saminathan Ponnusamy
Affiliation:
Department of Mathematics, Indian Institute of Technology Madras, Chennai, Tamilnadu, India
Qianghua Luo*
Affiliation:
School of Mathematics, Foshan University, Foshan, Guangdong Province, People’s Republic of China
*
Corresponding author: Qianghua Luoemail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a Gromov hyperbolic domain 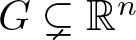$G\subsetneq \mathbb{R}^n$ with uniformly perfect Gromov boundary, Zhou and Rasila recently proved that for all quasiconformal homeomorphisms 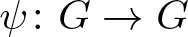$\psi\colon G\to G$ with identity value on the Gromov boundary, the quasihyperbolic displacement 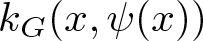$k_G(x,\psi(x))$ for all 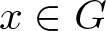$x\in G$ is bounded above. In this paper, we generalize this result and establish Teichmüller displacement theorem for quasi-isometries of Gromov hyperbolic spaces in a quantitative way. As applications, we obtain its connections to bilipschitz extensions of certain Gromov hyperbolic spaces.

Keywords

Gromov hyperbolic spaceTeichmüller displacement theoremquasi-isometryroughly starlikeuniformly perfect

MSC classification

Primary: 30L10: Quasiconformal mappings in metric spaces
Secondary: 30L05: Geometric embeddings of metric spaces
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 67 , Issue 4 , November 2024 , pp. 1148 - 1166
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bonfert–Taylor, P., Canary, R. D., Martin, G. and Taylor, E., Quasiconformal homogeneity of hyperbolic manifolds, Math. Ann. 331(2) (2005), 281–295.CrossRefGoogle Scholar
Bonk, M., Heinonen, J. and Koskela, P., Uniformizing Gromov hyperbolic spaces, Astérisque 270 (2001), .Google Scholar
Bonk, M. and Schramm, O., Embeddings of Gromov hyperbolic spaces, Geom. Funct. Anal. 10(2) (2000), 266–306.CrossRefGoogle Scholar
Bridson, M. and Haefliger, A., Metric Spaces of Non-Positive Curvature, Grundlehren der Mathematischen Wissenschaften, Volume 319, (Springer-Verlag, Berlin, 1999).CrossRefGoogle Scholar
Buyalo, S. and Schroeder, V., Elements of asymptotic geometry (EMS Monographs in Mathematics: Zürich, xii+200 pp. 2007).CrossRefGoogle Scholar
Gehring, F. W. and Osgood, B. G., Uniform domains and the quasi-hyperbolic metric, J. Anal. Math. 36 (1979), 50–74.CrossRefGoogle Scholar
Hästö, P., Gromov hyperbolicity of the jG and $\widetilde{j}_G$ metrics, Proc. Amer. Math. Soc. 134(4) (2006), 1137–1142.CrossRefGoogle Scholar
Hariri, P., Klén, R. and Vuorinen, M., Conformally invariant metrics and quasiconformal mappings. Springer Monographs in Mathematics, . (Springer, Cham, 2020).CrossRefGoogle Scholar
Heinonen, J., Lectures on Analysis on Metric Spaces (Springer-Verlag, Berlin-Heidelberg-New York, 2001).CrossRefGoogle Scholar
Herron, D., Shanmugalingam, N. and Xie, X., Uniformity from Gromov hyperbolicity, Illinois J. Math. 52(4) (2008), 1065–1109.CrossRefGoogle Scholar
Klén, R., Todorčević, V. and Vuorinen, M., Teichmüller’s problem in space, J. Math. Anal. Appl. 455(2) (2017), 1297–1316.CrossRefGoogle Scholar
Li, Y., Vuorinen, M. and Wang, X., Quasiconformal maps with bilipschitz or identity boundary values in Banach spaces, Ann. Acad. Sci. Fenn. Math. 39(2) (2014), 905–917.Google Scholar
Lukyanenko, A., Bi-Lipschitz extension from boundaries of certain hyperbolic spaces, Geom. Dedicata 164 (2013), 47–71.CrossRefGoogle Scholar
Manojlović, V. and Vuorinen, M., On quasiconformal maps with identity boundary values, Trans. Amer. Math. Soc. 363(4) (2011), 2467–2479.CrossRefGoogle Scholar
Rainio, O., Sugawa, T. and Vuorinen, M., Uniformly perfect sets, Hausdorff dimension, and conformal capacity, J. Geom. Anal. 34(6) (2024), , 10.1007/s12220-024-01599-5.CrossRefGoogle Scholar
Shanmugalingam, N. and Xie, X., A rigidity property of some negatively curved solvable Lie groups, Comment. Math. Helv. 87(4) (2012), 805–823.CrossRefGoogle Scholar
Sugawa, T., Uniformly perfect sets–analytic and geometric aspects, Sugaku 53(4) (2001), 387–402.Google Scholar
Sugawa, T., Vuorinen, M. and Zhang, T., Conformally invariant complete metrics, Math. Proc. Cambridge Philos. Soc. 174(2) (2023), 273–300.CrossRefGoogle Scholar
Teichmüller, O., Ein Verschiebungssatz der quasikonformen Abbildung, Deutsche Math, 7 (1944), 336–343.Google Scholar
Väisälä, J., Quasi-Möbius maps, J. Anal. Math. 44 (1984/85), 218–234.CrossRefGoogle Scholar
Väisälä, J., Gromov hyperbolic spaces, Expo. Math. 23(3) (2005), 187–231.CrossRefGoogle Scholar
Väisälä, J., Hyperbolic and uniform domains in Banach spaces, Ann. Acad. Sci. Fenn. Ser. A I Math. 30(2) (2005), 261–302.Google Scholar
Vuorinen, M. and Zhang, X., Distortion of quasiconformal mappings with identity boundary values, J. Lond. Math. Soc. 90(3) (2014), 637–653.CrossRefGoogle Scholar
Wang, X. and Zhou, Q., Quasimöbius maps, weakly quasimöbius maps and uniform perfectness in quasi-metric spaces, Ann. Acad. Sci. Fenn. Ser. AI Math. 42(1) (2017), 257–284.CrossRefGoogle Scholar
Xie, X., Quasiisometries between negatively curved Hadamard manifolds, J. Lond. Math. Soc. 79(1) (2009), 15–32.CrossRefGoogle Scholar
Xie, X., Quasisymmetric maps on the boundary of a negatively curved solvable Lie group, Math. Ann. 353(3) (2012), 727–746.CrossRefGoogle Scholar
Zhou, Q., Li, Y. and Rasila, A., Gromov hyperbolicity, John spaces, and quasihyperbolic geodesics, J. Geom. Anal. 32(9) (2022), .CrossRefGoogle Scholar
Zhou, Q., Ponnusamy, S. and Guan, T., Gromov hyperbolicity of the $\widetilde{j}_G$ metric and boundary correspondence, Proc. Amer. Math. Soc. 150(7) (2022), 2839–2847.CrossRefGoogle Scholar
Zhou, Q., Ponnusamy, S. and Rasila, A., Busemann functions and uniformization of Gromov hyperbolic spaces, https://arxiv.org/pdf/2008.01399v2.pdf.Google Scholar
Zhou, Q. and Rasila, A., Teichmüller’s problem for Gromov hyperbolic domains, Israel J. Math. 252(1) (2022), 399–427.CrossRefGoogle Scholar