Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bocci, Cristiano
Cooper, Susan
Guardo, Elena
Harbourne, Brian
Janssen, Mike
Nagel, Uwe
Seceleanu, Alexandra
Tuyl, Adam Van
and
Vu, Thanh
2016.
The Waldschmidt constant for squarefree monomial ideals.
Journal of Algebraic Combinatorics,
Vol. 44,
Issue. 4,
p.
875.
Akesseh, Solomon
2017.
Ideal containments under flat extensions.
Journal of Algebra,
Vol. 492,
Issue. ,
p.
44.
Gimenez, Philippe
Martínez-Bernal, José
Simis, Aron
Villarreal, Rafael H.
and
Vivares, Carlos E.
2018.
Singularities, Algebraic Geometry, Commutative Algebra, and Related Topics.
p.
491.
Szemberg, Tomasz
and
Szpond, Justyna
2018.
Multigraded Algebra and Applications.
Vol. 238,
Issue. ,
p.
159.
Hà, Huy Tài
and
Trung, Ngo Viet
2019.
Membership Criteria and Containments of Powers of Monomial Ideals.
Acta Mathematica Vietnamica,
Vol. 44,
Issue. 1,
p.
117.
Drabkin, Ben
Grifo, Eloísa
Seceleanu, Alexandra
and
Stone, Branden
2019.
Calculations involving symbolic powers.
Journal of Software for Algebra and Geometry,
Vol. 9,
Issue. 1,
p.
71.
Janssen, Mike
Kamp, Thomas
and
Vander Woude, Jason
2019.
Comparing powers of edge ideals.
Journal of Algebra and Its Applications,
Vol. 18,
Issue. 10,
p.
1950184.
Carlini, Enrico
Tài Hà, Huy
Harbourne, Brian
and
Van Tuyl, Adam
2020.
Ideals of Powers and Powers of Ideals.
Vol. 27,
Issue. ,
p.
81.
Hà, Huy Tài
Nguyen, Hop Dang
Trung, Ngo Viet
and
Trung, Tran Nam
2020.
Symbolic powers of sums of ideals.
Mathematische Zeitschrift,
Vol. 294,
Issue. 3-4,
p.
1499.
Carlini, Enrico
Tài Hà, Huy
Harbourne, Brian
and
Van Tuyl, Adam
2020.
Ideals of Powers and Powers of Ideals.
Vol. 27,
Issue. ,
p.
137.
Bisui, Sankhaneel
Hà, Huy Tài
Jayanthan, A. V.
and
Thomas, Abu Chackalamannil
2021.
Resurgence numbers of fiber products of projective schemes.
Collectanea Mathematica,
Vol. 72,
Issue. 3,
p.
605.
Dung, Le Xuan
Hien, Truong Thi
Nguyen, Hop D.
and
Trung, Tran Nam
2021.
Regularity and Koszul property of symbolic powers of monomial ideals.
Mathematische Zeitschrift,
Vol. 298,
Issue. 3-4,
p.
1487.
Ballico, Edoardo
Favacchio, Giuseppe
Guardo, Elena
Milazzo, Lorenzo
and
Thomas, Abu Chackalamannil
2021.
Steiner Configurations Ideals: Containment and Colouring.
Mathematics,
Vol. 9,
Issue. 3,
p.
210.
DiPasquale, Michael
and
Drabkin, Ben
2021.
On resurgence via asymptotic resurgence.
Journal of Algebra,
Vol. 587,
Issue. ,
p.
64.
Ballico, Edoardo
Favacchio, Giuseppe
Guardo, Elena
and
Milazzo, Lorenzo
2021.
Steiner systems and configurations of points.
Designs, Codes and Cryptography,
Vol. 89,
Issue. 2,
p.
199.
Bodas, Hrishikesh
Drabkin, Benjamin
Fong, Caleb
Jin, Su
Kim, Justin
Li, Wenxuan
Seceleanu, Alexandra
Tang, Tingting
and
Williams, Brendan
2021.
Consequences of the packing problem.
Journal of Algebraic Combinatorics,
Vol. 54,
Issue. 4,
p.
1095.
Grifo, Eloísa
and
Seceleanu, Alexandra
2021.
Commutative Algebra.
p.
343.
Mandal, Mousumi
and
Kumar Pradhan, Dipak
2021.
Symbolic powers in weighted oriented graphs.
International Journal of Algebra and Computation,
Vol. 31,
Issue. 03,
p.
533.
Camarneiro, João
Drabkin, Ben
Fragoso, Duarte
Frendreiss, William
Hoffman, Daniel
Seceleanu, Alexandra
Tang, Tingting
and
Yang, Sewon
2022.
Convex bodies and asymptotic invariants for powers of monomial ideals.
Journal of Pure and Applied Algebra,
Vol. 226,
Issue. 10,
p.
107089.
Camps-Moreno, Eduardo
Kohne, Craig
Sarmiento, Eliseo
and
Van Tuyl, Adam
2022.
Powers of Principal Q-Borel ideals.
Canadian Mathematical Bulletin,
Vol. 65,
Issue. 3,
p.
633.


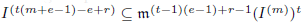 for all positive integers
for all positive integers 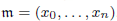 . This captures two conjectures (
. This captures two conjectures (