Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-22T16:52:44.530Z Has data issue: false hasContentIssue false
  • English
  • Français

A Study of the Length Function of Generalized Fractions of Modules

Part of: Commutative algebra: Homological methods Local rings and semilocal rings

Published online by Cambridge University Press:  02 November 2016

Marcel Morales  and
Pham Hung Quy
Marcel Morales
Affiliation:
Université de Grenoble I, Institut Fourier, UMR 5582, BP 74, 38402 Saint-Martin D’Hères, France ([email protected]) ESPE, Université Lyon 1, 5 rue Anselme, 69317 Lyon Cedex, France
Pham Hung Quy
Affiliation:
Department of Mathematics, FPT University, 8 Ton That Thuyet, Hanoi, Vietnam ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 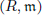be a Noetherian local ring and let M be a finitely generated R-module of dimension d. Let 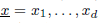be a system of parameters of M and let 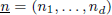be a d-tuple of positive integers. In this paper we study the length of generalized fractions M(1/(x1, … , xd, 1)), which was introduced by Sharp and Hamieh. First, we study the growth of the function

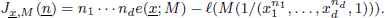
Then we give an explicit calculation for the function 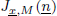in the case in which M admits a certain Macaulay extension. Most previous results on this topic are improved in a clearly understandable way.

Keywords

system of parametersgeneralized fractionslimit closurelocal cohomologyHilbert–Kunz function

MSC classification

Secondary: 13H15: Multiplicity theory and related topics 13D40: Hilbert-Samuel and Hilbert-Kunz functions; Poincaré series 13D45: Local cohomology
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 60 , Issue 3 , August 2017 , pp. 721 - 737
Copyright
Copyright © Edinburgh Mathematical Society 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Brenner, H., Irrational Hilbert–Kunz multiplicities, Preprint (arXiv:1305.5873v1 [math .AG]; 2013).Google Scholar
2. Cuong, N. T., On the dimension of the non-Cohen–Macaulay locus of local rings admitting dualizing complexes, Math. Proc. Camb. Phil. Soc. 109 (1991), 479–488.CrossRefGoogle Scholar
3. Cuong, N. T., On the least degree of polynomials bounding above the differences between lengths and multiplicities of certain system of parameters in local rings, Nagoya Math. J. 125 (1992), 105–114.Google Scholar
4. Cuong, N. T., p-standard systems of parameters and p-standard ideals in local rings, Acta Math. Vietnamica 20 (1995), 145–161.Google Scholar
5. Cuong, N. T. and Cuong, D. T., dd-sequences and partial Euler–Poincaré characteristics of Koszul complex, J. Alg. Appl. 6 (2007), 207–231.Google Scholar
6. Cuong, N. T. and Cuong, D. T., Local cohomology annihilators and Macaulayfication, Acta Math. Vietnamica (2016), DOI: 10.1007/s40306-016-0185-9.Google Scholar
7. Cuong, N. T. and Khoi, V. T., Module whose local cohomology modules have Cohen–Macaulay Matlis duals, in Commutative algebra, algebraic geometry and computational methods (ed. Eisenbud, D.), pp. 223–231 (Springer, 1999).Google Scholar
8. Cuong, N. T. and Minh, N. D., On the lengths of Koszul homology modules and generalized fractions, Math. Proc. Camb. Phil. Soc. 120 (1996), 31–42.CrossRefGoogle Scholar
9. Cuong, N. T. and Nhan, L. T., Pseudo Cohen–Macaulay and pseudo generalized Cohen–Macaulay module, J. Alg. 267 (2003), 156–177.Google Scholar
10. Cuong, N. T. and Quy, P. H., On the limit closure of sequence of elements in local rings, in Proc. 6th Japan–Vietnam Joint Seminar on Commutative Algebra, Hayama, Japan, pp. 127–135 (2010).Google Scholar
11. Cuong, N. T. and Quy, P. H., A splitting theorem for local cohomology and its applications, J. Alg. 331 (2011), 512–522.Google Scholar
12. Cuong, N. T. and Quy, P. H., On the splitting of local cohomology and the structure of finitely generated modules in local rings, in preparation.Google Scholar
13. Cuong, N. T., Hoa, N. T. and Loan, N. T. H., On certain length function associated to a system of parameters in local rings, Vietnam J. Math. 27 (1999), 259–272.Google Scholar
14. Cuong, N. T., Morales, M. and Nhan, L. T., On the length of generalized fractions. J. Alg. 265 (2003), 100–113.Google Scholar
15. Goto, S. and Nakamura, Y., Multiplicity and tight closures of parameters, J. Alg. 244 (2001), 302–311.CrossRefGoogle Scholar
16. Huneke, C., Theory of d-sequences and powers of ideals, Adv. Math. 46 (1982), 249–279.Google Scholar
17. Kunz, E., Characterizations of regular local rings of characteristic p , Am. J. Math. 91 (1969), 772–784.CrossRefGoogle Scholar
18. Minh, N. D., On the least degree of polynomials bounding above the differences between multiplicities and length of generalized fractions, Acta Math. Vietnamica 20 (1995), 115–128.Google Scholar
19. Monsky, P., The Hilbert–Kunz function, Math. Annalen 263 (1983), 43–49.CrossRefGoogle Scholar
20. Morales, M., On the S 2-fications of some toric varieties, Commun. Alg. 35 (2007), 2409–2430.Google Scholar
21. Morales, M. and Nhan, L. T., On length of generalized fractions , Vietnam J. Math. 31 (2003), 359–365.Google Scholar
22. Quy, P. H., On the splitting of local cohomology and applications, PhD thesis, Hanoi Institute of Mathematics (in Vietnamese, available at http://vie.math.ac.vn/learning/; 2013).Google Scholar
23. Schenzel, P., Dualisierende komplexe in der lokalen algebra und Buchsbaum-Ringe, Lecture Notes in Mathematics, Volume 907 (Springer, 1982).Google Scholar
24. Sharp, R. Y. and Hamieh, M. A., Length of certain generalized fractions, J. Pure Appl. Alg. 38 (1985), 323–336.Google Scholar
25. Sharp, R. Y. and Zakeri, H., Modules of generalized fractions, Mathematika 29 (1982), 32–41.Google Scholar
26. Trung, N. V., Absolutely superficial sequence, Math. Proc. Camb. Phil. Soc. 93(1) (1983), 35–47.Google Scholar
27. Trung, N. V., Toward a theory of generalized Cohen–Macaulay modules, Nagoya Math. J. 102 (1986), 1–49.CrossRefGoogle Scholar