Hostname: page-component-669899f699-8p65j Total loading time: 0 Render date: 2025-04-25T02:11:11.542Z Has data issue: false hasContentIssue false
  • English
  • Français

On quasi and weak Steinberg characters of general linear groups

Part of: Linear algebraic groups and related topics Representation theory of groups

Published online by Cambridge University Press:  19 December 2024

Surinder Kaur Open the ORCID record for Surinder Kaur [Opens in a new window]
Surinder Kaur*
Affiliation:
Department of Mathematics, School of Engineering and Sciences, SRM University-AP, Guntur, Andhra Pradesh, India
*
Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a finite group and r be a prime divisor of the order of G. An irreducible character of G is said to be quasi r-Steinberg if it is non-zero on every r-regular element of G. A quasi r-Steinberg character of degree 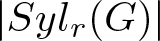$\displaystyle |Syl_r(G)|$ is said to be weak r-Steinberg if it vanishes on the r-singular elements of 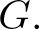$G.$ In this article, we classify the quasi r-Steinberg cuspidal characters of the general linear group 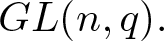$GL(n,q).$ Then we characterize the quasi r-Steinberg characters of 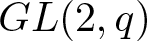$GL(2,q)$ and 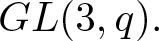$GL(3,q).$ Finally, we obtain a classification of the weak r-Steinberg characters of 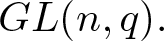$GL(n,q).$

Keywords

general linear groupcuspidal characterSteinberg characterparabolic induction

MSC classification

Primary: 20C15: Ordinary representations and characters
Secondary: 20G05: Representation theory 20C33: Representations of finite groups of Lie type
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , First View , pp. 1 - 18
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Basheer, A. B. M., Character tables of the general linear group and some of its subgroups, M.Sc. Thesis (University of KwaZulu-Natal, Pietermaritzburg, 2008).Google Scholar
Bump, D., Lie Groups, second edition, Graduate Texts in Mathematics (Springer, New York, NY, 2013).CrossRefGoogle Scholar
Curtis, C. W., The Steinberg character of a finite group with a (B, N)-pair, J. Algebra 4 (1966), 433–441.CrossRefGoogle Scholar
Darafsheh, M. R., p-Steinberg characters of alternating and projective special linear groups, J. Algebra 181(1) (1996), 196–206.CrossRefGoogle Scholar
Feit, W., Extending Steinberg characters, in Linear algebraic groups and their representations (Los Angeles CA, 1992), Contemporary Mathematics, Volume 153, (American Mathematical Society, Providence, RI, 1993).Google Scholar
Green, J. A., The characters of the finite general linear groups, Trans. Amer. Math. Soc. 80 (1955), 402–447.CrossRefGoogle Scholar
Green, J. A., Discrete series characters for GL(n,q), Algebr. Represent. Theory 2(1) (1999), 61–82.CrossRefGoogle Scholar
Humphreys, J. E., The Steinberg representation, Bull. Amer. Math. Soc. (N.S.) 16(2) (1987), 247–263.CrossRefGoogle Scholar
Malle, G. and Zalesski, A., Steinberg-like characters for finite simple groups, J. Group Theory 23(1) (2020), 25–78.CrossRefGoogle Scholar
Malle, G. and Zalesskii, A. E., Prime power degree representations of quasi-simple groups, Arch. Math. (Basel) 77(6) (2001), 461–468.CrossRefGoogle Scholar
Mishra, A., Paul, D. and Singla, P., On quasi Steinberg characters of complex reflection groups, Algebr. Represent. Theory 26(6) (2023), 3101–3118.CrossRefGoogle Scholar
Paul, D. and Singla, P., On quasi Steinberg characters of symmetric and alternating groups and their double covers, J. Algebra Appl. 21(10) (2022), .CrossRefGoogle Scholar
Pellegrini, M. A. and Zalesski, A. E., On characters of Chevalley groups vanishing at the non-semisimple elements, Internat. J. Algebra Comput. 26(4) (2016), 789–841.CrossRefGoogle Scholar
Roitman, M., On Zsigmondy primes, Proc. Amer. Math. Soc. 125(7) (1997), 1913–1919.CrossRefGoogle Scholar
Steinberg, R., The representations of GL(3,q), GL(4,q), PGL(3,q) and PGL(4,q), Canad. J. Math. 3 (1951), 225–235.CrossRefGoogle Scholar
Steinberg, R., Prime power representations of finite linear groups, Canad. J. Math 8 (1956), 580–591.CrossRefGoogle Scholar
Steinberg, R., Prime power representations of finite linear groups. II, Canad. J. Math. 9 (1957), 347–351.CrossRefGoogle Scholar
Tiep, P. H., p-Steinberg characters of finite simple groups, J. Algebra 187(1) (1997), 304–319.CrossRefGoogle Scholar