Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T03:05:14.610Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on the Fundamental Group of Kodaira Fibrations

Part of: Surfaces and higher-dimensional varieties Differential topology

Published online by Cambridge University Press:  30 January 2019

Stefano Vidussi
Stefano Vidussi*
Affiliation:
Department of Mathematics, University of California, Riverside, CA 92521, USA ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

The fundamental group π of a Kodaira fibration is, by definition, the extension of a surface group 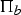$\Pi_b$ by another surface group 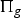$\Pi _g$, i.e.

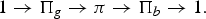$$1 \rightarrow \Pi_g \rightarrow \pi \rightarrow \Pi_b \rightarrow 1.$$
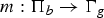Conversely, Catanese (2017) inquires about what conditions need to be satisfied by a group of that sort in order to be the fundamental group of a Kodaira fibration. In this short note we collect some restrictions on the image of the classifying map $m \colon \Pi_b \to \Gamma_g$ in terms of the coinvariant homology of 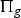$\Pi_g$. In particular, we observe that if π is the fundamental group of a Kodaira fibration with relative irregularity g−s, then 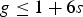$g \leq 1+ 6s$, and we show that this effectively constrains the possible choices for π, namely that there are group extensions as above that fail to satisfy this bound, hence it cannot be the fundamental group of a Kodaira fibration. A noteworthy consequence of this construction is that it provides examples of symplectic 4-manifolds that fail to admit a Kähler structure for reasons that eschew the usual obstructions.

Keywords

Kodaira fibrationssurface bundles over a surfaceKaehler groups

MSC classification

Primary: 14J29: Surfaces of general type
Secondary: 57R17: Symplectic and contact topology
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 62 , Issue 3 , August 2019 , pp. 739 - 746
Copyright
Copyright © Edinburgh Mathematical Society 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Arapura, D., Toward the structure of fibered fundamental groups of projective varieties, J. Éc. polytech. Math. 4 (2017), 595–611.Google Scholar
2Barja, M. Á., González–Alonso, V. and Naranjo, J. C., Xiao's conjecture for general fibred surfaces, J. Reine Angew. Math. 739 (2018), 297–308.Google Scholar
3Barth, W., Hulek, K., Peters, C. and Van de Ven, A., Compact complex surfaces, 2nd edn, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics, Volume 4 (Springer-Verlag, Berlin, 2004).Google Scholar
4Baykur, R. İ., Non-holomorphic surface bundles and Lefschetz fibrations, Math. Res. Lett. 19 (2012), 567–574.Google Scholar
5Baykur, R. İ. and Margalit, D., Indecomposable surface bundles over surfaces, J. Topol. Anal. 5 (2013), 161–181.Google Scholar
6Beauville, A., L'inégalité $p_g \geq 2q-4$ pour les surfaces de type général, Appendix to O. Debarre, Inégalités numériques pour les surfaces de type général, Bull. Soc. Math. France 110(3) (1982), 319–346.Google Scholar
7Catanese, F., Kodaira fibrations and beyond: methods for moduli theory, Jpn. J. Math. 12(2) (2017), 91–174.Google Scholar
8Endo, H., Korkmaz, M., Kotschick, D., Ozbagci, B. and Stipsicz, A., Commutators, Lefschetz fibrations and the signatures of surface bundles, Topology 41 (2002), 961–977.Google Scholar
9Flapan, L., Monodromy of Kodaira fibrations of genus 3, preprint (arXiv:1709.03164, 2017).Google Scholar
10Hillman, J., Complex surfaces which are fibre bundle, Topology Appl. 100 (2000), 187–191.Google Scholar
11Hillman, J., Sections of surface bundles, in Interactions between low-dimensional topology and mapping class groups (ed. Inanc Baykur, R., Etnyre, John and Hamenstädt, Ursula), pp. 1–20, Geometry and Topology Monographs, Volume 19 (Mathematical Sciences, 2015).Google Scholar
12Johnson, F. E. A., A class of non-Kählerian manifolds, Math. Proc. Cambridge Philos. Soc. 100(3) (1986), 519–521.Google Scholar
13Kotschick, D., On regularly fibered complex surfaces, in Proceedings of the Kirbyfest (Berkeley, CA, 1998) (ed. Hass, Joel and Scharlemann, Martin), pp. 291–298, Geometry and Topology Monographs, Volume 2 (Mathematical Sciences, 1999).Google Scholar
14Liu, K., Geometric height inequalities, Math. Res. Lett. 3 (1996), 693–702.Google Scholar
15Rolfsen, D., Knots and links, corrected reprint of the 1976 original, Mathematics Lecture Series, Volume 7 (Publish or Perish, Houston, TX, 1990), xiv+439 pp.Google Scholar
16Thurston, W., Some simple examples of symplectic manifolds, Proc. Amer. Math. Soc. 55(2) (1976), 467–468.Google Scholar
17Wall, C. T. C. (ed.) List of problems, in Homological group theory (Proc. Sympos., Durham, 1977), London Mathematical Society Lecture Note Series,Volume 36 (Cambridge University Press, 1979).Google Scholar
18Xiao, G., Fibred algebraic surfaces with low slope, Math. Ann. 276 (1987), 449–466.Google Scholar