Published online by Cambridge University Press: 28 June 2023
The Fueter-Sce theorem provides a procedure to obtain axially monogenic functions, which are in the kernel of generalized Cauchy–Riemann operator in 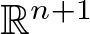 ${\mathbb{R}}^{n+1}$. This result is obtained by using two operators. The first one is the slice operator, which extends holomorphic functions of one complex variable to slice monogenic functions in
${\mathbb{R}}^{n+1}$. This result is obtained by using two operators. The first one is the slice operator, which extends holomorphic functions of one complex variable to slice monogenic functions in  $ \mathbb{R}^{n+1}$. The second one is a suitable power of the Laplace operator in n + 1 variables. Another way to get axially monogenic functions is the generalized Cauchy–Kovalevskaya (CK) extension. This characterizes axial monogenic functions by their restriction to the real line. In this paper, using the connection between the Fueter-Sce map and the generalized CK-extension, we explicitly compute the actions
$ \mathbb{R}^{n+1}$. The second one is a suitable power of the Laplace operator in n + 1 variables. Another way to get axially monogenic functions is the generalized Cauchy–Kovalevskaya (CK) extension. This characterizes axial monogenic functions by their restriction to the real line. In this paper, using the connection between the Fueter-Sce map and the generalized CK-extension, we explicitly compute the actions 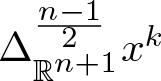 $\Delta_{\mathbb{R}^{n+1}}^{\frac{n-1}{2}} x^k$, where
$\Delta_{\mathbb{R}^{n+1}}^{\frac{n-1}{2}} x^k$, where 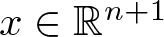 $x \in \mathbb{R}^{n+1}$. The expressions obtained is related to a well-known class of Clifford–Appell polynomials. These are the building blocks to write a Taylor series for axially monogenic functions. By using the connections between the Fueter-Sce map and the generalized CK extension, we characterize the range and the kernel of the Fueter-Sce map. Furthermore, we focus on studying the Clifford–Appell–Fock space and the Clifford–Appell–Hardy space. Finally, using the polyanalytic Fueter-Sce theorems, we obtain a new family of polyanalytic monogenic polynomials, which extends to higher dimensions the Clifford–Appell polynomials.
$x \in \mathbb{R}^{n+1}$. The expressions obtained is related to a well-known class of Clifford–Appell polynomials. These are the building blocks to write a Taylor series for axially monogenic functions. By using the connections between the Fueter-Sce map and the generalized CK extension, we characterize the range and the kernel of the Fueter-Sce map. Furthermore, we focus on studying the Clifford–Appell–Fock space and the Clifford–Appell–Hardy space. Finally, using the polyanalytic Fueter-Sce theorems, we obtain a new family of polyanalytic monogenic polynomials, which extends to higher dimensions the Clifford–Appell polynomials.