Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-11T05:22:34.337Z Has data issue: false hasContentIssue false
  • English
  • Français

Fourier transforms related to ζ(s)

Part of: Harmonic analysis in one variable Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  30 April 2021

Pablo A. Panzone
Pablo A. Panzone*
Affiliation:
Departamento e Instituto de Matematica, Universidad Nacional del Sur, Av. Alem 1253, 8000Bahia Blanca, Argentina ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Using some formulas of S. Ramanujan, we compute in closed form the Fourier transform of functions related to Riemann zeta function $\zeta (s)=\sum \nolimits _{n=1}^{\infty } {1}/{n^{s}}$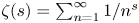 and other Dirichlet series.

Keywords

Fourier transformDirichlet Seriesintegralssupported in part by UNS and CONICET

MSC classification

Primary: 42A38: Fourier and Fourier-Stieltjes transforms and other transforms of Fourier type
Secondary: 11M99: None of the above, but in this section
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 2 , May 2021 , pp. 200 - 216
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Báez-Duarte, L., A strengthening of the Nyman-Beurling criterion for the Riemann Hypothesis, Atti Acad. Naz. Lincei Rend. Lincei Mat. Appl. 14 (2003), 5–11.Google Scholar
Báez-Duarte, L., Balazard, M., Landreau, B. and Saias, E., Notes sur la fonction $\zeta$ de Riemann III, Adv. Math. 149 (2000), 130–144.CrossRefGoogle Scholar
Berndt, B., Ramanujan's Notebooks, Part II (Springer, 1989).CrossRefGoogle Scholar
Berndt, B., Ramanujan's Notebooks, Part V (Springer, 1997).Google Scholar
Beurling, A., A closure problem related to the Riemann zeta-function, Proc. Nat. Acad. Sci. 41 (1955), 312–314.CrossRefGoogle ScholarPubMed
Dimitrov, Dimitar K. and Rusev, Peter K., Zeros of entire Fourier Transforms, East J. Approx. 17(1) (2011), 1–110.Google Scholar
Dimitrov, Dimitar K. and Xu, Y., Wronskians of Fourier and Laplace transforms, Trans. Amer.Math. Soc. 372 (2019), 4107–4125.CrossRefGoogle Scholar
Donoghue, W. F., Distributions and Fourier Transforms (Academic Press, 1969).Google Scholar
Edwards, H. M., Riemann's Zeta Function (Dover Publications, 2001).Google Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory (AMS, 2004).Google Scholar
Nyman, B., On Some Groups and Semigroups of Translations, Thesis (Uppsala, 1950).Google Scholar
Panzone, P. A., Formulas for the Riemann Zeta-function and certain Dirichlet series, Int. Trans. Special Funct. 29 (2018), 893–908.CrossRefGoogle Scholar
van der Pol, B., An electro-mechanical investigation of the Riemann zeta function in the critical strip, Bull. Amer. Math. Soc. 53 (1947), 976–981.CrossRefGoogle Scholar
Ramanujan, S., Collected Papers (Cambridge University Press, Cambridge, 1927). reprinted by Chelsea, New York, 1962; reprinted by the AMS (Providence, RI, 2000).Google Scholar
Titchmarsh, E. C., The theory of Riemann Zeta-Function, edited and with a preface by D. R. Heath-Brown (Oxford Science Publications, 1986).Google Scholar