Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T16:01:00.337Z Has data issue: false hasContentIssue false
  • English
  • Français

Divisorial Models of Normal Varieties

Part of: Surfaces and higher-dimensional varieties Computational aspects in algebraic geometry (Co)homology theory

Published online by Cambridge University Press:  31 January 2017

Stefano Urbinati
Stefano Urbinati*
Affiliation:
Università degli Studi di Padova, Dipartimento di Matematica, Room 630, Via Trieste 63, 35121 Padova, Italy ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

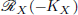We prove that the canonical ring of a canonical variety in the sense of de Fernex and Hacon is finitely generated. We prove that canonical varieties are Kawamata log terminal (klt) if and only if is finitely generated. We introduce a notion of nefness for non-ℚ-Gorenstein varieties and study some of its properties. We then focus on these properties for non-ℚ-Gorenstein toric varieties.

Keywords

normal varietiessingularities of pairspositivitytoric varieties

MSC classification

Secondary: 14J17: Singularities 14F18: Multiplier ideals 14Q15: Higher-dimensional varieties
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 60 , Issue 4 , November 2017 , pp. 1053 - 1064
Copyright
Copyright © Edinburgh Mathematical Society 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Ambro, F., The set of toric minimal log discrepancies, Central Eur. J. Math. 4 (2006), 358–370.Google Scholar
2. Birkar, C., Cascini, P., Hacon, C. D. and McKernan, J., Existence of minimal models for varieties of log general type, J. Am. Math. Soc. 23(2) (2006), 405–468.Google Scholar
3. Boucksom, S., de Fernex, T. and Favre, C., The volume of an isolated singularity, Duke Math. J. 161(8) (2012), 1455–1520.Google Scholar
4. Chiecchio, A. and Urbinati, S., Ample Weil divisors, J. Alg. 437 (2015), 202–221.Google Scholar
5. Cox, D. A., Little, J. B. and Schenck, H. K., Toric varieties, Graduate Studies in Mathematics, Volume 124 (American Mathematical Society, Providence, RI, 2011).Google Scholar
6. de Fernex, T. and Hacon, C. D., Singularities on normal varieties, Compositio Math. 145(2) (2009), 393–414.Google Scholar
7. Elizondo, E. J., The ring of global sections of multiples of a line bundle on a toric variety, Proc. Am. Math. Soc. 125(9) (1997), 2527–2529.CrossRefGoogle Scholar
8. Fujino, O., Notes on toric varieties from Mori theoretic viewpoint, Tohoku Math. J. 55(4) (2003), 551–564.Google Scholar
9. Kollár, J., Exercises in the birational geometry of algebraic varieties, Preprint (arXiv: 0809.2579; 2008).Google Scholar
10. Kollár, J. and Mori, S., Birational geometry of algebraic varieties (in collaboration with Clemens, C. H. and Corti, A.; translation of 1998 Japanese original), Cambridge Tracts in Mathematics, Volume 134 (Cambridge University Press, 1998).Google Scholar
11. Lin, H.-W., Combinatorial method in adjoint linear systems on toric varieties, Michigan Math. J. 51 (2003), 491–501.Google Scholar
12. Urbinati, S., Discrepancies of non-ℚ-Gorenstein varieties, Michigan Math. J. 61(2) (2012), 265–277.Google Scholar