No CrossRef data available.
Published online by Cambridge University Press: 22 November 2022
We study the asymptotic behaviour of the periodically mixed Zaremba problem. We cover the part of the boundary by a chess board with a small period (square size) $\varepsilon$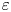 and impose the Dirichlet condition on black and the Neumann condition on white squares. As $\varepsilon \to 0$
and impose the Dirichlet condition on black and the Neumann condition on white squares. As $\varepsilon \to 0$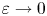 , we get the effective boundary condition which is always of the Dirichlet type. The Dirichlet data on the boundary, however, depend on the ratio between the magnitudes of the two boundary values.
, we get the effective boundary condition which is always of the Dirichlet type. The Dirichlet data on the boundary, however, depend on the ratio between the magnitudes of the two boundary values.