Published online by Cambridge University Press: 13 February 2015
We prove that every incidence graph of a finite projective plane allows a partitioning into incident point-line pairs. This is used to determine the order of the identity in the K0-group of so-called polygonal algebras associated with cocompact group actions on Ã2-buildings with three orbits. These C*-algebras are classified by the K0-group and the class 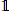 of the identity in K0. To be more precise, we show that 2(q − 1)
of the identity in K0. To be more precise, we show that 2(q − 1) 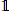 = 0, where q is the order of the links of the building. Furthermore, if q = 22l−1 with l ∈ ℤ, then the order of
= 0, where q is the order of the links of the building. Furthermore, if q = 22l−1 with l ∈ ℤ, then the order of 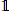 is q − 1.
is q − 1.