Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T03:21:18.309Z Has data issue: false hasContentIssue false
  • English
  • Français

Borg's Periodicity Theorems for First-Order Self-Adjoint Systems with Complex Potentials

Part of: General theory in ordinary differential equations Boundary value problems Ordinary differential operators

Published online by Cambridge University Press:  19 December 2016

Sonja Currie ,
Thomas T. Roth  and
Bruce A. Watson
Sonja Currie
Affiliation:
School of Mathematics, University of the Witwatersrand, Private Bag 3, PO Wits 2050, South Africa ([email protected])
Thomas T. Roth
Affiliation:
School of Mathematics, University of the Witwatersrand, Private Bag 3, PO Wits 2050, South Africa ([email protected])
Bruce A. Watson
Affiliation:
School of Mathematics, University of the Witwatersrand, Private Bag 3, PO Wits 2050, South Africa ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

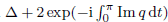A self-adjoint first-order system with Hermitian π-periodic potential Q(z), integrable on compact sets, is considered. It is shown that all zeros of are double zeros if and only if this self-adjoint system is unitarily equivalent to one in which Q(z) is π/2-periodic. Furthermore, the zeros of 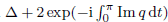are all double zeros if and only if the associated self-adjoint system is unitarily equivalent to one in which Q(z) = σ2Q(z)σ2. Here, Δ denotes the discriminant of the system and σ0, σ2 are Pauli matrices. Finally, it is shown that all instability intervals vanish if and only if Q = rσ0 + qσ2, for some real-valued π-periodic functions r and q integrable on compact sets.

Keywords

Dirac systeminverse problemsspectral theory

MSC classification

Secondary: 34A55: Inverse problems 34L40: Particular operators (Dirac, one-dimensional Schrödinger, etc.) 34B05: Linear boundary value problems
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 60 , Issue 3 , August 2017 , pp. 615 - 633
Copyright
Copyright © Edinburgh Mathematical Society 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Ambarzumyan, V. A., Über eine Frage der Eigenwerttheorie, Z. Phys. 53 (1912), 690–695.CrossRefGoogle Scholar
2. Amour, L., Inverse spectral theory for the AKNS system with separated boundary conditions, Inv. Probl. 9 (1993), 503–523.CrossRefGoogle Scholar
3. Amour, L. and Guillot, J.-C., Isospectral sets for AKNS systems on the unit interval with generalised periodic boundary conditions, Geom. Funct. Analysis 6 (1996), 1–27.Google Scholar
4. Asano, N. and Kato, Y., Algebraic and spectral methods for nonlinear wave equations (Longman, New York, 1990).Google Scholar
5. Boonserm, P. and Visser, M., Reformulating the Schrödinger equation as a Shabat–Zakharov system, J. Math. Phys. 51(2) (2010), 022105.Google Scholar
6. Borg, G., Eine Umkehrung der Sturm–Liouvillschen Eigenwertaufgabe: Bestimmung der Differentialgleichung durch die Eigenwerte, Acta Math. 78 (1946), 1–96.Google Scholar
7. Brown, M. B., Eastham, M. S. P. and Schmidt, K. M., Periodic differential operators (Birkhäuser, 2013).CrossRefGoogle Scholar
8. Cherednik, I., Basic methods of soliton theory (World Scientific, 1996).Google Scholar
9. Clark, S. and Gesztesy, F., Weyl–Titchmarsh M-function asymptotics, local uniqueness results, trace formulas, and Borg-type theorems for Dirac operators, J. Lond. Math. Soc. 74 (2006), 757–777.Google Scholar
10. Clark, S., Gesztesy, F., Holden, H. and Levitan, B. M., Borg-type theorems for matrix-valued Schrödinger operators, J. Diff. Eqns 167 (2000), 181–210.CrossRefGoogle Scholar
11. Clark, S., Gesztesy, F. and Renger, W., Trace formulas and Borg-type theorems for matrix-valued Jacobi and Dirac finite difference operators, J. Diff. Eqns 219 (2005), 144–182.Google Scholar
12. Coddington, E. A. and Levinson, N., Theory of ordinary differential equations (McGraw-Hill, 1955).Google Scholar
13. Desaix, M., Anderson, D., Helczynski, L. and Lisak, M., Eigenvalues of the Zakharov–Shabat scattering problem for real symmetric pulses, Phys. Rev. Lett. 90(1) (2003), 013901.Google Scholar
14. Dickey, L. A., Soliton equations and Hamiltonian systems (World Scientific, 1991).Google Scholar
15. Dubrovin, B. A., Completely integrable Hamiltonian systems associated with matrix operators and Abelian varieties, Funct. Analysis Applic. 11 (1977), 265–277.CrossRefGoogle Scholar
16. Freiling, G. and Yurko, V. A., Inverse Sturm–Liouville problems and applications (Nova Science, 2001).Google Scholar
17. Gasymov, M. G. and Dzabiev, T. T., The inverse problem for the Dirac system, Dokl. Akad. Nauk SSSR 167 (1966), 967–970.Google Scholar
18. Gasymov, M. G. and Dzabiev, T. T., Solution of the inverse problem by two spectra for the Dirac equation on a finite interval, Akad. Nauk Azerbuidzan. SSR Dokl. 22 (1966), 3–6.Google Scholar
19. Gasymov, M. G. and Dzabiev, T. T., Determination of the system of Dirac differential equations from two spectra, in Proc. of the Summer School in the Spectral Theory of Operators and the Theory of Group Representations, Baku, 1968, pp. 3–6.Google Scholar
20. Gerdjikov, V. S., Vilasi, G. and Yanovski, A. B., The inverse scattering problem for the Zakharov–Shabat system, in Integrable Hamiltonian hierarchies: spectral and geometric methods, Lecture Notes in Physics, Volume 748, pp. 97–132 (Springer, 2008).Google Scholar
21. Gesztesy, F. and Zinchenko, M., A Borg-type theorem associated with orthogonal polynomials on the unit circle, J. Lond. Math. Soc. 74 (2006), 757–777.Google Scholar
22. Gesztesy, F., Kiselev, A. and Makarov, K. A., Uniquness results for matrix-valued Schrödinger, Jacobi and Dirac-type operators, Math. Machr. 239–240 (2002), 103–145.Google Scholar
23. Hochstadt, H., On the determination of a Hill's equation from its spectrum, Arch. Ration. Mech. Analysis 19 (1965), 353–362.Google Scholar
24. Hochstadt, H., On a Hill's equation with double eigenvalues, Proc. Am. Math. Soc. 65 (1977), 373–374.Google Scholar
25. Hochstadt, H., A direct and inverse problem for a Hill's equation with double eigenvalues, J. Math. Analysis Applic. 66 (1978), 507–513.CrossRefGoogle Scholar
26. Hörmander, L., Lectures on nonlinear hyperbolic differential equations, Mathématiques & Applications, Volume 26 (Springer, 1997).Google Scholar
27. Kriss, M., An n-dimensional Ambarzumian type theorem for Dirac operators, Inv. Probl. 20 (2004), 1593–1597.Google Scholar
28. Lesch, M. and Malamud, M., The inverse spectral problem for first order systems on the half line, in Operator theory, systems theory, and related topics: the Moshe anniversary volume (ed. Alpay, D. and Vinnikov, V.), pp. 199-238, Operatory Theory: Advances and Applications, Volume 117 (Birkhäuser, 2000).Google Scholar
29. Levitan, B. M. and Sargsjan, I. S., Sturm–Liouville and Dirac operators (Kluwer, 1991).Google Scholar
30. Sakhnovich, A. L., Spectral theory of canonical differential systems: method of operator identities, Operator Theory: Advances and Applications, Volume 107 (Birkhäuser, 1999).Google Scholar
31. Sakhnovich, A. L., Dirac type and canonical systems: spectral and Weyl–Titchmarch functions, direct and inverse problems, Inv. Probl. 18 (2002), 331–348.Google Scholar
32. Serier, F., Inverse spectral problems for singular Ablowitz–Kaup–Newell–Segur operators on [0, 1], Inv. Probl. 22 (2006), 1457–1484.Google Scholar
33. Watson, B. A., Inverse spectral problems for weighted Dirac systems, Inv. Probl. 15 (1999), 793–805.Google Scholar
34. Yang, C.-F. and Yang, X.-P., Some Ambarzumyan-type theorems for Dirac operators, Inv. Probl. 23 (2007), 2565–2574.Google Scholar