Article contents
Bilattices and Morita Equivalence of MASA Bimodules
Published online by Cambridge University Press: 20 November 2015
Abstract
We define an equivalence relation between bimodules over maximal abelian self-adjoint algebras (MASA bimodules), which we call spatial Morita equivalence. We prove that two reflexive MASA bimodules are spatially Morita equivalent if and only if their (essential) bilattices are isomorphic. We also prove that if 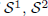 are bilattices that correspond to reflexive MASA bimodules
are bilattices that correspond to reflexive MASA bimodules 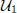 ,
, 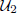 and
and 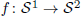 is an onto bilattice homomorphism, then
is an onto bilattice homomorphism, then
(i) if 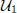 is synthetic, then
is synthetic, then 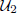 is synthetic;
is synthetic;
(ii) if 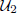 contains a non-zero compact (or a finite or a rank 1) operator, then
contains a non-zero compact (or a finite or a rank 1) operator, then 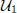 also contains a non-zero compact (or a finite or a rank 1) operator.
also contains a non-zero compact (or a finite or a rank 1) operator.
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 59 , Issue 3 , August 2016 , pp. 605 - 621
- Copyright
- Copyright © Edinburgh Mathematical Society 2015
References
- 2
- Cited by


