No CrossRef data available.
Article contents
An example regarding Kalton's paper ‘isomorphisms between spaces of vector-valued continuous functions’
Published online by Cambridge University Press: 02 August 2021
Abstract
The paper alluded to in the title contains the following striking result: Let $I$ be the unit interval and $\Delta$
be the unit interval and $\Delta$ the Cantor set. If $X$
the Cantor set. If $X$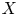 is a quasi Banach space containing no copy of $c_{0}$
is a quasi Banach space containing no copy of $c_{0}$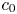 which is isomorphic to a closed subspace of a space with a basis and $C(I,\,X)$
which is isomorphic to a closed subspace of a space with a basis and $C(I,\,X)$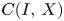 is linearly homeomorphic to $C(\Delta ,\, X)$
is linearly homeomorphic to $C(\Delta ,\, X)$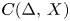 , then $X$
, then $X$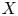 is locally convex, i.e., a Banach space. We will show that Kalton result is sharp by exhibiting non-locally convex quasi Banach spaces $X$
is locally convex, i.e., a Banach space. We will show that Kalton result is sharp by exhibiting non-locally convex quasi Banach spaces $X$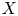 with a basis for which $C(I,\,X)$
with a basis for which $C(I,\,X)$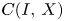 and $C(\Delta ,\, X)$
and $C(\Delta ,\, X)$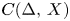 are isomorphic. Our examples are rather specific and actually, in all cases, $X$
are isomorphic. Our examples are rather specific and actually, in all cases, $X$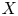 is isomorphic to $C(K,\,X)$
is isomorphic to $C(K,\,X)$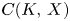 if $K$
if $K$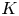 is a metric compactum of finite covering dimension.
is a metric compactum of finite covering dimension.
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 3 , August 2021 , pp. 615 - 619
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society



