No CrossRef data available.
Article contents
The abelianization of the elementary group of rank two
Published online by Cambridge University Press: 20 January 2025
Abstract
For an arbitrary ring A, we study the abelianization of the elementary group 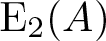 $\mathit{{\rm E}}_2(A)$. In particular, we show that for a commutative ring A there exists an exact sequence
$\mathit{{\rm E}}_2(A)$. In particular, we show that for a commutative ring A there exists an exact sequence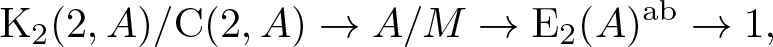 \begin{equation*}{\rm K}_2(2,A)/{\rm C}(2,A) \rightarrow A/M \rightarrow \mathit{{\rm E}}_2(A)^{\rm ab} \rightarrow 1,\end{equation*}
\begin{equation*}{\rm K}_2(2,A)/{\rm C}(2,A) \rightarrow A/M \rightarrow \mathit{{\rm E}}_2(A)^{\rm ab} \rightarrow 1,\end{equation*}
where 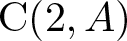 ${\rm C}(2,A)$ is the central subgroup of the Steinberg group
${\rm C}(2,A)$ is the central subgroup of the Steinberg group 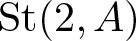 $\mathit{{\rm St}}(2,A)$ generated by the Steinberg symbols and M is the additive subgroup of A generated by
$\mathit{{\rm St}}(2,A)$ generated by the Steinberg symbols and M is the additive subgroup of A generated by 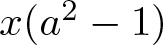 $x(a^2-1)$ and
$x(a^2-1)$ and 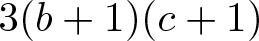 $3(b+1)(c+1)$, with
$3(b+1)(c+1)$, with 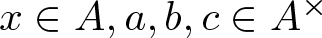 $x\in A, a,b,c \in {A^\times}$.
$x\in A, a,b,c \in {A^\times}$.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.
References
 $\mathit{{\rm SL}}_2(\mathbb{Z}[\frac{1}{m}])$, Journal of Algebra, 660 (2024), .Google Scholar
$\mathit{{\rm SL}}_2(\mathbb{Z}[\frac{1}{m}])$, Journal of Algebra, 660 (2024), .Google Scholar


