Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T17:54:00.013Z Has data issue: false hasContentIssue false
  • English
  • Français

2-subnormal quadratic offenders and Oliver's p-group conjecture

Part of: Representation theory of groups

Published online by Cambridge University Press:  10 December 2012

Justin Lynd
Justin Lynd*
Affiliation:
Department of Mathematics, The Ohio State University, Columbus, OH 43210, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Bob Oliver conjectures that if p is an odd prime and S is a finite p-group, then the Oliver subgroup 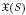contains the Thompson subgroup Je(S). A positive resolution of this conjecture would give the existence and uniqueness of centric linking systems for fusion systems at odd primes. Using the ideas and work of Glauberman, we prove that if p ≥ 5, G is a finite p-group, and V is an elementary abelian p-group which is an F-module for G, then there exists a quadratic offender which is 2-subnormal (normal in its normal closure) in G. We apply this to show that Oliver's Conjecture holds provided that the quotient 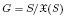has class at most log2(p − 2) + 1, or p ≥ 5 and G is equal to its own Baumann subgroup.

Keywords

p-groupquadratic offenderp-local finite group

MSC classification

Secondary: 20D15: Nilpotent groups, $p$-groups 20C20: Modular representations and characters
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 56 , Issue 1 , February 2013 , pp. 211 - 222
Copyright
Copyright © Edinburgh Mathematical Society 2012

References

1.Broto, C., Levi, R. and Oliver, B., Homotopy equivalences of p-completed classifying spaces of finite groups, Invent. Math. 151(3) (2003), 611–664.CrossRefGoogle Scholar
2.Broto, C., Levi, R. and Oliver, B., The theory of p-local groups: a survey, in Homotopy theory: relations with algebraic geometry, group cohomology, and algebraic K theory, Contemporary Mathematics, Volume 346, pp. 51–84 (American Mathematical Society, Providence, RI, 2004).Google Scholar
3.Chermak, A., Fusion systems and localities, Preprint (2012).Google Scholar
4.Glauberman, G., Large abelian subgroups of finite p-groups, J. Alg. 196 (1997), 301–338.CrossRefGoogle Scholar
5.Gorenstein, D., Lyons, R. and Solomon, R., The classification of the finite simple groups, Number 2, Part I, Chapter G, Mathematical Surveys and Monographs, Volume 40 (American Mathematical Society, Providence, RI, 1996).Google Scholar
6.Green, D. J., Héthelyi, L. and Lilienthal, M., On Oliver's p-group conjecture, Alg. Number Theory 2 (2008), 969–977.CrossRefGoogle Scholar
7.Green, D. J., Héthelyi, L. and Mazza, N., On Oliver's p-group conjecture, II, Math. Annalen 347(1) (2010), 111–122.CrossRefGoogle Scholar
8.Green, D. J., Héthelyi, L. and Mazza, N., On a strong form of Oliver's p-group conjecture, J. Alg. 342 (2011), 1–15.CrossRefGoogle Scholar
9.Huppert, B. and Blackburn, N., Finite groups, III (Springer, 1982).CrossRefGoogle Scholar
10.Meierfrankenfeld, U., Stellmacher, B. and Stroth, G., Finite groups of local characteristic p: an overview, in Groups, Combinatorics and Geometry, Durham, 2001, pp. 155–192 (World Scientific, River Edge, NJ, 2003).CrossRefGoogle Scholar
11.Oliver, B., Equivalences of classifying spaces completed at odd primes, Math. Proc. Camb. Phil. Soc. 137(2) (2004), 321–347.CrossRefGoogle Scholar