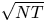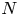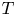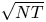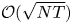1. Introduction
In this note, we consider the problem of assortment optimization under the multinomial logit (MNL) choice model with a capacity constraint on the size of the assortment and incomplete information about the model parameters. This problem has recently received considerable attention in the literature (see, e.g., [Reference Agrawal, Avadhanula, Goyal and Zeevi1–Reference Kallus and Udell7,Reference Rusmevichientong, Shen and Shmoys9,Reference Sauré and Zeevi10]).
Two notable recent contributions are from Agrawal et al. [Reference Agrawal, Avadhanula, Goyal and Zeevi1,Reference Agrawal, Avadhanula, Goyal and Zeevi2], who construct decision policies based on Thompson Sampling and Upper Confidence Bounds, respectively, and show that the regret of these policies—the cumulative expected revenue loss compared with the benchmark of always offering an optimal assortment—is, up to logarithmic terms, bounded by a constant times ![]() $\sqrt {N T}$, where
$\sqrt {N T}$, where ![]() $N$ denotes the number of products and
$N$ denotes the number of products and ![]() $T\geqslant N$ denotes the length of the time horizon. These upper bounds are complemented by the recent work from Chen and Wang [Reference Chen and Wang3], who show that the regret of any policy is bounded from below by a positive constant times
$T\geqslant N$ denotes the length of the time horizon. These upper bounds are complemented by the recent work from Chen and Wang [Reference Chen and Wang3], who show that the regret of any policy is bounded from below by a positive constant times ![]() $\sqrt {N T}$, implying that the policies by Agrawal et al. [Reference Agrawal, Avadhanula, Goyal and Zeevi1,Reference Agrawal, Avadhanula, Goyal and Zeevi2] are (up to logarithmic terms) asymptotically optimal.
$\sqrt {N T}$, implying that the policies by Agrawal et al. [Reference Agrawal, Avadhanula, Goyal and Zeevi1,Reference Agrawal, Avadhanula, Goyal and Zeevi2] are (up to logarithmic terms) asymptotically optimal.
The lower bound by Chen and Wang [Reference Chen and Wang3] is proven under the assumption that the product revenues are constant—that is, each product generates the same amount of revenue when sold. In practice, it often happens that different products have different marginal revenues, and it is a priori not completely clear whether the policies by Agrawal et al. [Reference Agrawal, Avadhanula, Goyal and Zeevi1,Reference Agrawal, Avadhanula, Goyal and Zeevi2] are still asymptotically optimal or that a lower regret can be achieved. In addition, Chen and Wang [Reference Chen and Wang3] assume that ![]() $K$, the maximum number of products allowed in an assortment, is bounded by
$K$, the maximum number of products allowed in an assortment, is bounded by ![]() $\tfrac {1}{4} \cdot N$, but point out that this constant
$\tfrac {1}{4} \cdot N$, but point out that this constant ![]() $\tfrac {1}{4}$ can probably be increased.
$\tfrac {1}{4}$ can probably be increased.
In this note, we settle this open question by proving a ![]() $\sqrt {N T}$ regret lower bound for any given vector of product revenues. This implies that policies with
$\sqrt {N T}$ regret lower bound for any given vector of product revenues. This implies that policies with ![]() ${{\mathcal {O}}}(\sqrt {N T})$ regret are asymptotically optimal regardless of the product revenue parameters. Furthermore, our result is valid for all
${{\mathcal {O}}}(\sqrt {N T})$ regret are asymptotically optimal regardless of the product revenue parameters. Furthermore, our result is valid for all ![]() $K < \tfrac {1}{2} N$, thereby confirming the intuition of Chen and Wang [Reference Chen and Wang3] that the constraint
$K < \tfrac {1}{2} N$, thereby confirming the intuition of Chen and Wang [Reference Chen and Wang3] that the constraint ![]() $K \leqslant \tfrac {1}{4} N$ is not tight.
$K \leqslant \tfrac {1}{4} N$ is not tight.
2. Model and main result
We consider the problem of dynamic assortment optimization under the MNL choice model. In this model, the number of products is ![]() $N \in {{\mathbb {N}}}$. Henceforth, we abbreviate the set of products
$N \in {{\mathbb {N}}}$. Henceforth, we abbreviate the set of products ![]() $\{1\ldots ,N\}$ as
$\{1\ldots ,N\}$ as ![]() $[N]$. Each product
$[N]$. Each product ![]() $i\in [N]$ yields a known marginal revenue to the seller of
$i\in [N]$ yields a known marginal revenue to the seller of ![]() $w_i> 0$. Without loss of generality due to scaling, we can assume that
$w_i> 0$. Without loss of generality due to scaling, we can assume that ![]() $w_i\leqslant 1$ for all
$w_i\leqslant 1$ for all ![]() $i\in [N]$. Each product
$i\in [N]$. Each product ![]() $i\in [N]$ is associated with a preference parameter
$i\in [N]$ is associated with a preference parameter ![]() $v_i\geqslant 0$, unknown to the seller. Each offered assortment
$v_i\geqslant 0$, unknown to the seller. Each offered assortment ![]() $S\subseteq [N]$ must satisfy a capacity constraint, that is,
$S\subseteq [N]$ must satisfy a capacity constraint, that is, ![]() $|S|\leqslant K$ for capacity constraint
$|S|\leqslant K$ for capacity constraint ![]() $K \in {{\mathbb {N}}}$,
$K \in {{\mathbb {N}}}$, ![]() $K\leqslant N$. For notational convenience, we write
$K\leqslant N$. For notational convenience, we write
for the collection of all assortments of size at most ![]() $K$, and
$K$, and
for the collection of all assortments of exact size ![]() $K$. Let
$K$. Let ![]() $T \in {{\mathbb {N}}}$ denote a finite time horizon. Then, at each time
$T \in {{\mathbb {N}}}$ denote a finite time horizon. Then, at each time ![]() $t\in [T]$, the seller selects an assortment
$t\in [T]$, the seller selects an assortment ![]() $S_t\in \mathcal {A}_K$ based on the purchase information available up to and including time
$S_t\in \mathcal {A}_K$ based on the purchase information available up to and including time ![]() $t-1$. Thereafter, the seller observes a single purchase
$t-1$. Thereafter, the seller observes a single purchase ![]() $Y_t\in S_t\cup \{0\}$, where product
$Y_t\in S_t\cup \{0\}$, where product ![]() $0$ indicates a no-purchase. The purchase probabilities within the MNL model are given by
$0$ indicates a no-purchase. The purchase probabilities within the MNL model are given by
for all ![]() $t \in [T]$ and
$t \in [T]$ and ![]() $i \in S \cup \{0\}$, where we write
$i \in S \cup \{0\}$, where we write ![]() $v_0 := 1$. The assortment decisions of the seller are described by his/her policy: a collection of probability distributions
$v_0 := 1$. The assortment decisions of the seller are described by his/her policy: a collection of probability distributions ![]() $\pi = (\pi (\,\cdot \,|\,h) : h \in H)$ on
$\pi = (\pi (\,\cdot \,|\,h) : h \in H)$ on ![]() $\mathcal {A}_K$, where
$\mathcal {A}_K$, where
is the set of possible histories. Then, conditionally on ![]() $h=(S_1, Y_1, \ldots , S_{t-1}, Y_{t-1})$, assortment
$h=(S_1, Y_1, \ldots , S_{t-1}, Y_{t-1})$, assortment ![]() $S_t$ has distribution
$S_t$ has distribution ![]() $\pi (\,\cdot \,|\,h)$, for all
$\pi (\,\cdot \,|\,h)$, for all ![]() $h \in H$ and all
$h \in H$ and all ![]() $t \in [T]$. Let
$t \in [T]$. Let ![]() $\mathbb {E}^{\pi }_v$ be the expectation operator under policy
$\mathbb {E}^{\pi }_v$ be the expectation operator under policy ![]() $\pi$ and preference vector
$\pi$ and preference vector ![]() $v\in \mathcal {V} := [0, \infty )^{N}$. The objective for the seller is to find a policy
$v\in \mathcal {V} := [0, \infty )^{N}$. The objective for the seller is to find a policy ![]() $\pi$ that maximizes the total accumulated revenue or, equivalently, minimizes the accumulated regret:
$\pi$ that maximizes the total accumulated revenue or, equivalently, minimizes the accumulated regret:
 $$\Delta_{\pi}(T, v) := T \cdot \max_{S \in \mathcal{A}_K} r(S, v) - \sum_{t=1}^{T} \mathbb{E}^{\pi}_v [ r(S_t, v)],$$
$$\Delta_{\pi}(T, v) := T \cdot \max_{S \in \mathcal{A}_K} r(S, v) - \sum_{t=1}^{T} \mathbb{E}^{\pi}_v [ r(S_t, v)],$$where ![]() $r(S,v)$ is the expected revenue of assortment
$r(S,v)$ is the expected revenue of assortment ![]() $S\subseteq [N]$ under preference vector
$S\subseteq [N]$ under preference vector ![]() $v \in \mathcal {V}$:
$v \in \mathcal {V}$:
In addition, we define the worst-case regret:
The main result, presented below, states that the regret of any policy can uniformly be bounded from below by a constant times ![]() $\sqrt {NT}$.
$\sqrt {NT}$.
Theorem 1 Suppose that ![]() $K < N / 2$. Then, there exists a constant
$K < N / 2$. Then, there exists a constant ![]() $c_1 > 0$ such that, for all
$c_1 > 0$ such that, for all ![]() $T \geqslant N$ and for all policies
$T \geqslant N$ and for all policies ![]() $\pi$,
$\pi$,
3. Proof of Theorem 1
3.1. Proof outline
The proof of Theorem 1 can be broken up into four steps. First, we define a baseline preference vector ![]() $v^{0}\in \mathcal {V}$ and we show that under
$v^{0}\in \mathcal {V}$ and we show that under ![]() $v^{0}$ any assortment
$v^{0}$ any assortment ![]() $S\in \mathcal {S}_K$ is optimal. Second, for each
$S\in \mathcal {S}_K$ is optimal. Second, for each ![]() $S\in \mathcal {A}_K$, we define a preference vector
$S\in \mathcal {A}_K$, we define a preference vector ![]() $v^{S}\in \mathcal {V}$ by
$v^{S}\in \mathcal {V}$ by
for some ![]() $\epsilon \in (0,1]$. For each such
$\epsilon \in (0,1]$. For each such ![]() $v^{S}$, we show that the instantaneous regret from offering a suboptimal assortment
$v^{S}$, we show that the instantaneous regret from offering a suboptimal assortment ![]() $S_t$ is bounded from below by a constant times the number of products
$S_t$ is bounded from below by a constant times the number of products ![]() $|S \setminus S_t|$ not in
$|S \setminus S_t|$ not in ![]() $S$; cf. Lemma 1 below. This lower bound takes into account how much the assortments
$S$; cf. Lemma 1 below. This lower bound takes into account how much the assortments ![]() $S_1,\ldots ,S_T$ overlap with
$S_1,\ldots ,S_T$ overlap with ![]() $S$ when the preference vector is
$S$ when the preference vector is ![]() $v^{S}$. Third, let
$v^{S}$. Third, let ![]() $N_i$ denote the number of times product
$N_i$ denote the number of times product ![]() $i\in [N]$ is contained
$i\in [N]$ is contained ![]() $S_1,\ldots ,S_T$, that is,
$S_1,\ldots ,S_T$, that is,
 $$N_i:= \sum_{t=1}^{T} \textbf{1}\{i\in S_t\}.$$
$$N_i:= \sum_{t=1}^{T} \textbf{1}\{i\in S_t\}.$$Then, we use the Kullback–Leibler (KL) divergence and Pinsker's inequality to upper bound the difference between the expected value of ![]() $N_i$ under
$N_i$ under ![]() $v^{S}$ and
$v^{S}$ and ![]() $v^{S\backslash \{i\}}$, see Lemma 2. Fourth, we apply a randomization argument over
$v^{S\backslash \{i\}}$, see Lemma 2. Fourth, we apply a randomization argument over ![]() $\{v^{S}:S\in \mathcal {S}_K\}$, we combine the previous steps, and we set
$\{v^{S}:S\in \mathcal {S}_K\}$, we combine the previous steps, and we set ![]() $\epsilon$ accordingly to conclude the proof.
$\epsilon$ accordingly to conclude the proof.
The novelty of this work is concentrated in the first two steps. The third and fourth step closely follow the work of Chen and Wang [Reference Chen and Wang3]. These last steps are included (1) because of slight deviations in our setup, (2) for the sake of completeness, and (3) since the proof techniques are extended to the case where ![]() $K/N<1/2$. In the work of Chen and Wang [Reference Chen and Wang3], the lower bound is shown for
$K/N<1/2$. In the work of Chen and Wang [Reference Chen and Wang3], the lower bound is shown for ![]() $K/N\leqslant 1/4$, but the authors already mention that this constraint can probably be relaxed. Our proof confirms that this is indeed the case.
$K/N\leqslant 1/4$, but the authors already mention that this constraint can probably be relaxed. Our proof confirms that this is indeed the case.
3.2. Step 1: Construction of the baseline preference vector
Let ![]() $\underline {w} := \min _{i\in [N]} w_i>0$ and define the constant
$\underline {w} := \min _{i\in [N]} w_i>0$ and define the constant
Note that ![]() $s<\underline {w}$. The baseline preference vector is formally defined as
$s<\underline {w}$. The baseline preference vector is formally defined as
Now, the expected revenue for any ![]() $S\in \mathcal {A}_K$ under
$S\in \mathcal {A}_K$ under ![]() $v^{0}$ can be rewritten as
$v^{0}$ can be rewritten as
 $$r(S,v^{0}) = \frac{\sum_{i\in S}v^{0}_i w_i}{1 + \sum_{i\in S}v^{0}_i} = \frac{ s\sum_{i\in S} \frac{w_i}{w_i-s}}{ K + \sum_{i\in S} \frac{s}{w_i-s}} = \frac{ s\sum_{i\in S} \frac{w_i}{w_i-s}}{ K - |S| + \sum_{i\in S} \frac{w_i}{w_i-s}}.$$
$$r(S,v^{0}) = \frac{\sum_{i\in S}v^{0}_i w_i}{1 + \sum_{i\in S}v^{0}_i} = \frac{ s\sum_{i\in S} \frac{w_i}{w_i-s}}{ K + \sum_{i\in S} \frac{s}{w_i-s}} = \frac{ s\sum_{i\in S} \frac{w_i}{w_i-s}}{ K - |S| + \sum_{i\in S} \frac{w_i}{w_i-s}}.$$The expression on the right-hand side is only maximized by assortments ![]() $S$ with maximal size
$S$ with maximal size ![]() $|S| = K$, in which case
$|S| = K$, in which case
It follows that all assortments ![]() $S$ with size
$S$ with size ![]() $K$ are optimal.
$K$ are optimal.
3.3. Step 2: Lower bound on the instantaneous regret of  $v^{S}$
$v^{S}$
For the second step, we bound the instantaneous regret under ![]() $v^{S}$.
$v^{S}$.
Lemma 1 Let ![]() $S\in \mathcal {S}_K$. Then, there exists a constant
$S\in \mathcal {S}_K$. Then, there exists a constant ![]() $c_2>0$, only depending on
$c_2>0$, only depending on ![]() $\underline {w}$ and
$\underline {w}$ and ![]() $s$, such that, for all
$s$, such that, for all ![]() $t\in [T]$ and
$t\in [T]$ and ![]() $S_t\in \mathcal {A}_K$,
$S_t\in \mathcal {A}_K$,
As a consequence,
 \begin{equation} T \cdot \max_{S'\in \mathcal{A}_K} r(S', v^{S}) - \sum_{t=1}^{T} r(S_t,v^{S}) \geqslant c_2\,\epsilon\left(T - \frac{1}{K}\sum_{i\in S}N_i\right). \end{equation}
\begin{equation} T \cdot \max_{S'\in \mathcal{A}_K} r(S', v^{S}) - \sum_{t=1}^{T} r(S_t,v^{S}) \geqslant c_2\,\epsilon\left(T - \frac{1}{K}\sum_{i\in S}N_i\right). \end{equation}Proof. Fix ![]() $S\in \mathcal {S}_K$. First, note that since
$S\in \mathcal {S}_K$. First, note that since ![]() $\epsilon \leqslant 1$, for any
$\epsilon \leqslant 1$, for any ![]() $S'\in \mathcal {A}_K$, it holds that
$S'\in \mathcal {A}_K$, it holds that
Second, let ![]() $S^{*}\in \textrm {arg max}_{S'\in \mathcal {A}_K}\,r(S',v^{S})$ and
$S^{*}\in \textrm {arg max}_{S'\in \mathcal {A}_K}\,r(S',v^{S})$ and ![]() $\varrho ^{*} = r(S^{*},v^{S})$. By rewriting the inequality
$\varrho ^{*} = r(S^{*},v^{S})$. By rewriting the inequality ![]() $\varrho ^{*}\geqslant r(S',v^{S})$ for all
$\varrho ^{*}\geqslant r(S',v^{S})$ for all ![]() $S'\in \mathcal {A}_K$, we find that for all
$S'\in \mathcal {A}_K$, we find that for all ![]() $S'\in \mathcal {A}_K$
$S'\in \mathcal {A}_K$
Let ![]() $t\in [T]$ and
$t\in [T]$ and ![]() $S_t\in \mathcal {A}_K$. Then, it holds that
$S_t\in \mathcal {A}_K$. Then, it holds that
 \begin{align*} r(S^{*},v^{S}) - r(S_t,v^{S}) & = \varrho^{*} - \frac{\sum_{i\in S_t} v^{S}_i w_i}{1 + \sum_{i\in S_t} v^{S}_i} \\ & = \frac{1}{1 + \sum_{i\in S_t} v^{S}_i}\left(\varrho^{*} + \sum_{i\in S_t} v^{S}_i\varrho^{*} - \sum_{i\in S_t} v^{S}_i w_i\right)\\ & \geqslant \frac{\underline{w}-s}{\underline{w}+s}\left(\varrho^{*} - \sum_{i\in S_t} v^{S}_i(w_i-\varrho^{*})\right)\\ & \geqslant \frac{\underline{w}-s}{\underline{w}+s}\left(\sum_{i\in S} v^{S}_i(w_i-\varrho^{*}) - \sum_{i\in S_t} v^{S}_i(w_i-\varrho^{*})\right) \\ & = \frac{\underline{w}-s}{\underline{w}+s} \left(\vphantom{\sum_{i\in S}}\right. \underbrace{\sum_{i\in S} v^{S}_i(w_i-s) - \sum_{i\in S_t} v^{S}_i(w_i-s)}_{(a)} \\ & \quad- \underbrace{(\varrho^{*}-s)\left( \sum_{i\in S} v^{S}_i - \sum_{i\in S_t} v^{S}_i\right)}_{(b)} \left.\vphantom{\sum_{i\in S}}\right). \end{align*}
\begin{align*} r(S^{*},v^{S}) - r(S_t,v^{S}) & = \varrho^{*} - \frac{\sum_{i\in S_t} v^{S}_i w_i}{1 + \sum_{i\in S_t} v^{S}_i} \\ & = \frac{1}{1 + \sum_{i\in S_t} v^{S}_i}\left(\varrho^{*} + \sum_{i\in S_t} v^{S}_i\varrho^{*} - \sum_{i\in S_t} v^{S}_i w_i\right)\\ & \geqslant \frac{\underline{w}-s}{\underline{w}+s}\left(\varrho^{*} - \sum_{i\in S_t} v^{S}_i(w_i-\varrho^{*})\right)\\ & \geqslant \frac{\underline{w}-s}{\underline{w}+s}\left(\sum_{i\in S} v^{S}_i(w_i-\varrho^{*}) - \sum_{i\in S_t} v^{S}_i(w_i-\varrho^{*})\right) \\ & = \frac{\underline{w}-s}{\underline{w}+s} \left(\vphantom{\sum_{i\in S}}\right. \underbrace{\sum_{i\in S} v^{S}_i(w_i-s) - \sum_{i\in S_t} v^{S}_i(w_i-s)}_{(a)} \\ & \quad- \underbrace{(\varrho^{*}-s)\left( \sum_{i\in S} v^{S}_i - \sum_{i\in S_t} v^{S}_i\right)}_{(b)} \left.\vphantom{\sum_{i\in S}}\right). \end{align*}Here, the first inequality is due to (3.3) and the second inequality follows from (3.4) with ![]() $S'=S$. Next, note that since
$S'=S$. Next, note that since ![]() $|S_t|\leqslant K$ and
$|S_t|\leqslant K$ and ![]() $|S|=K$, we find that
$|S|=K$, we find that
Now, term ![]() $(a)$ can be bounded from below as
$(a)$ can be bounded from below as
 \begin{align} (a) & = \sum_{i\in S\backslash S_t} v^{S}_i(w_i-s) - \sum_{i\in S_t\backslash S} v^{S}_i(w_i-s) \nonumber\\ & = \frac{s}{K}((1+\epsilon)|S\backslash S_t| - |S_t\backslash S|) \nonumber\\ & \geqslant s \,\frac{\epsilon\,|S\backslash S_t|}{K}. \end{align}
\begin{align} (a) & = \sum_{i\in S\backslash S_t} v^{S}_i(w_i-s) - \sum_{i\in S_t\backslash S} v^{S}_i(w_i-s) \nonumber\\ & = \frac{s}{K}((1+\epsilon)|S\backslash S_t| - |S_t\backslash S|) \nonumber\\ & \geqslant s \,\frac{\epsilon\,|S\backslash S_t|}{K}. \end{align}Here, at the final inequality, we used (3.5). Next, term ![]() $(b)$ can be bounded from above as
$(b)$ can be bounded from above as
 $$(b) \leqslant \underbrace{|\varrho^{*}-s|}_{(c)}\,\underbrace{\left| \sum_{i\in S} v^{S}_i - \sum_{i\in S_t} v^{S}_i\right|}_{(d)}.$$
$$(b) \leqslant \underbrace{|\varrho^{*}-s|}_{(c)}\,\underbrace{\left| \sum_{i\in S} v^{S}_i - \sum_{i\in S_t} v^{S}_i\right|}_{(d)}.$$Now, for term ![]() $(c)$, we note that
$(c)$, we note that ![]() $v^{S}_i\geqslant v^{0}_i$ for all
$v^{S}_i\geqslant v^{0}_i$ for all ![]() $i\in [N]$. In addition, since
$i\in [N]$. In addition, since ![]() $r(S^{*},v^{0})\leqslant s$,
$r(S^{*},v^{0})\leqslant s$,
 \begin{align*} \varrho^{*} - s & \leqslant \frac{\sum_{i\in S^{*}}v^{S}_i w_i}{1 + \sum_{i\in S^{*}}v^{S}_i} - \frac{\sum_{i\in S^{*}}v^{0}_i w_i}{1 + \sum_{i\in S^{*}}v^{0}_i}\\ & \leqslant \frac{1}{1 + \sum_{i\in S^{*}}v^{0}_i}\sum_{i\in S^{*}}(v^{S}_i-v^{0}_i)w_i\\ & \leqslant \sum_{i=1}^{N}(v^{S}_i-v^{0}_i) = \epsilon\sum_{i\in S}v^{0}_i \leqslant \frac{s}{\underline{w} - s} \epsilon. \end{align*}
\begin{align*} \varrho^{*} - s & \leqslant \frac{\sum_{i\in S^{*}}v^{S}_i w_i}{1 + \sum_{i\in S^{*}}v^{S}_i} - \frac{\sum_{i\in S^{*}}v^{0}_i w_i}{1 + \sum_{i\in S^{*}}v^{0}_i}\\ & \leqslant \frac{1}{1 + \sum_{i\in S^{*}}v^{0}_i}\sum_{i\in S^{*}}(v^{S}_i-v^{0}_i)w_i\\ & \leqslant \sum_{i=1}^{N}(v^{S}_i-v^{0}_i) = \epsilon\sum_{i\in S}v^{0}_i \leqslant \frac{s}{\underline{w} - s} \epsilon. \end{align*}This entails an upper bound for ![]() $(c)$. Term
$(c)$. Term ![]() $(d)$ is bounded from above as
$(d)$ is bounded from above as
 \begin{align*} (d)& \leqslant \sum_{i\in S\backslash S_t} v^{S}_i + \sum_{i\in S_t\backslash S} v^{S}_i \\ & \leqslant (1+\epsilon)\sum_{i\in S\backslash S_t} v^{0}_i + \sum_{i\in S_t\backslash S} v^{0}_i \\ & \leqslant (1+\epsilon)\frac{s}{K(\underline{w} - s)}|S\backslash S_t| + \frac{s}{K(\underline{w} - s)}|S_t\backslash S|\\ & \leqslant \frac{3s}{\underline{w} - s} \frac{|S\backslash S_t|}{K}. \end{align*}
\begin{align*} (d)& \leqslant \sum_{i\in S\backslash S_t} v^{S}_i + \sum_{i\in S_t\backslash S} v^{S}_i \\ & \leqslant (1+\epsilon)\sum_{i\in S\backslash S_t} v^{0}_i + \sum_{i\in S_t\backslash S} v^{0}_i \\ & \leqslant (1+\epsilon)\frac{s}{K(\underline{w} - s)}|S\backslash S_t| + \frac{s}{K(\underline{w} - s)}|S_t\backslash S|\\ & \leqslant \frac{3s}{\underline{w} - s} \frac{|S\backslash S_t|}{K}. \end{align*}Here, at the final inequality, we used (3.5) and the fact that ![]() $\epsilon \leqslant 1$. Now, we combine the upper bounds of
$\epsilon \leqslant 1$. Now, we combine the upper bounds of ![]() $(c)$ and
$(c)$ and ![]() $(d)$ to find that
$(d)$ to find that
It follows from (3.6) and (3.7) that
 \begin{align*} r(S^{*},v^{S}) - r(S_t,v^{S}) & \geqslant \frac{\underline{w}-s}{\underline{w}+s}\left(s -\frac{3s^{2}}{(\underline{w} -s)^{2}}\right)\frac{\epsilon |S\backslash S_t|}{K}\\ & \geqslant c_2 \frac{\epsilon|S\backslash S_t|}{K}, \end{align*}
\begin{align*} r(S^{*},v^{S}) - r(S_t,v^{S}) & \geqslant \frac{\underline{w}-s}{\underline{w}+s}\left(s -\frac{3s^{2}}{(\underline{w} -s)^{2}}\right)\frac{\epsilon |S\backslash S_t|}{K}\\ & \geqslant c_2 \frac{\epsilon|S\backslash S_t|}{K}, \end{align*}where
Note that the constant ![]() $c_2$ is positive if
$c_2$ is positive if ![]() $(\underline {w}-s)^{2}>3s$. This follows from
$(\underline {w}-s)^{2}>3s$. This follows from ![]() $s=\underline {w}^{2}/(3+2\underline {w})$ since
$s=\underline {w}^{2}/(3+2\underline {w})$ since
Statement (3.2) follows from the additional observation
 $$\sum_{t=1}^{T} |S\backslash S_t| = TK - \sum_{t=1}^{T} |S\cap S_t|= TK - \sum_{i\in S}N_i.$$
$$\sum_{t=1}^{T} |S\backslash S_t| = TK - \sum_{t=1}^{T} |S\cap S_t|= TK - \sum_{i\in S}N_i.$$3.4. Step 3: KL divergence and Pinsker's inequality
We denote the dependence of the expected value and the probability on the preference vector ![]() $v^{S}$ as
$v^{S}$ as ![]() $\mathbb {E}_S[\,\cdot \,]$ and
$\mathbb {E}_S[\,\cdot \,]$ and ![]() ${{\mathbb {P}}}_S(\cdot )$ for
${{\mathbb {P}}}_S(\cdot )$ for ![]() $S\in \mathcal {A}_K$. In addition, we write
$S\in \mathcal {A}_K$. In addition, we write ![]() $S \backslash i$ instead of
$S \backslash i$ instead of ![]() $S \backslash \{i\}$. The lemma below states an upper bound on the KL divergence of
$S \backslash \{i\}$. The lemma below states an upper bound on the KL divergence of ![]() ${{\mathbb {P}}}_S$ and
${{\mathbb {P}}}_S$ and ![]() ${{\mathbb {P}}}_{S\backslash i}$ and uses Pinsker's inequality to derive an upper bound on the absolute difference between the expected value of
${{\mathbb {P}}}_{S\backslash i}$ and uses Pinsker's inequality to derive an upper bound on the absolute difference between the expected value of ![]() $N_i$ under
$N_i$ under ![]() $v^{S}$ and
$v^{S}$ and ![]() $v^{S\backslash i}$.
$v^{S\backslash i}$.
Lemma 2 Let ![]() $S\in \mathcal {S}_K$,
$S\in \mathcal {S}_K$, ![]() $S'\in \mathcal {A}_K$, and
$S'\in \mathcal {A}_K$, and ![]() $i\in S$. Then, there exists a constant
$i\in S$. Then, there exists a constant ![]() $c_3$, only depending on
$c_3$, only depending on ![]() $\underline {w}$ and
$\underline {w}$ and ![]() $s$, such that
$s$, such that
As a consequence,
Proof. Let ![]() ${{\mathbb {P}}}$ and
${{\mathbb {P}}}$ and ![]() ${{\mathbb {Q}}}$ be arbitrary probability measures on
${{\mathbb {Q}}}$ be arbitrary probability measures on ![]() $S'\cup \{0\}$. It can be shown, see, for example, Lemma 3 from Chen and Wang [Reference Chen and Wang3], that
$S'\cup \{0\}$. It can be shown, see, for example, Lemma 3 from Chen and Wang [Reference Chen and Wang3], that
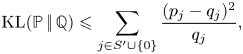 $${\textrm{KL}}({{\mathbb{P}}}\,|\!|\,{{\mathbb{Q}}}) \leqslant \sum_{j\in S'\cup\{0\}} \frac{(p_j-q_j)^{2}}{q_j},$$
$${\textrm{KL}}({{\mathbb{P}}}\,|\!|\,{{\mathbb{Q}}}) \leqslant \sum_{j\in S'\cup\{0\}} \frac{(p_j-q_j)^{2}}{q_j},$$where ![]() $p_j$ and
$p_j$ and ![]() $q_j$ are the probabilities of outcome
$q_j$ are the probabilities of outcome ![]() $j$ under
$j$ under ![]() ${{\mathbb {P}}}$ and
${{\mathbb {P}}}$ and ![]() ${{\mathbb {Q}}}$, respectively. We apply this result for
${{\mathbb {Q}}}$, respectively. We apply this result for ![]() $p_j$ and
$p_j$ and ![]() $q_j$ defined as
$q_j$ defined as
 $$p_j := \frac{v^{S}_j}{1+\sum_{\ell\in S'}v^{S}_\ell} \quad\text{and}\quad q_j := \frac{v^{S\backslash i}_j}{1+\sum_{\ell\in S'}v^{S\backslash i}_\ell},$$
$$p_j := \frac{v^{S}_j}{1+\sum_{\ell\in S'}v^{S}_\ell} \quad\text{and}\quad q_j := \frac{v^{S\backslash i}_j}{1+\sum_{\ell\in S'}v^{S\backslash i}_\ell},$$for ![]() $j\in S'\cup \{0\}$. First, note that by (3.3), for all
$j\in S'\cup \{0\}$. First, note that by (3.3), for all ![]() $j\in S'\cup \{0\}$,
$j\in S'\cup \{0\}$,
 $$q_j\geqslant \frac{v^{0}_j}{1 + 2\frac{s}{\underline{w} - s}} = \frac{\underline{w} - s}{\underline{w}+s}v^{0}_j.$$
$$q_j\geqslant \frac{v^{0}_j}{1 + 2\frac{s}{\underline{w} - s}} = \frac{\underline{w} - s}{\underline{w}+s}v^{0}_j.$$Now, we bound ![]() $|p_j-q_j|$ from above for
$|p_j-q_j|$ from above for ![]() $j\in S'\cup \{0\}$. Note that for
$j\in S'\cup \{0\}$. Note that for ![]() $j=0$ it holds that
$j=0$ it holds that
 \begin{align*} |p_0-q_0| & = \frac{|\sum_{\ell\in S'}v^{S}_\ell - \sum_{\ell\in S'}v^{S\backslash i}_\ell|}{(1 + \sum_{\ell\in S'}v^{S}_\ell)(1 + \sum_{\ell\in S'}v^{S\backslash i}_\ell)}\\ & \leqslant |(1+\epsilon)v^{0}_i - v^{0}_i| = v^{0}_i \epsilon. \end{align*}
\begin{align*} |p_0-q_0| & = \frac{|\sum_{\ell\in S'}v^{S}_\ell - \sum_{\ell\in S'}v^{S\backslash i}_\ell|}{(1 + \sum_{\ell\in S'}v^{S}_\ell)(1 + \sum_{\ell\in S'}v^{S\backslash i}_\ell)}\\ & \leqslant |(1+\epsilon)v^{0}_i - v^{0}_i| = v^{0}_i \epsilon. \end{align*}For ![]() $j\neq i$, since
$j\neq i$, since ![]() $\epsilon \leqslant 1$, we find that
$\epsilon \leqslant 1$, we find that
For ![]() $j=i$, we find that
$j=i$, we find that
 \begin{align*} |p_i-q_i| & = v^{0}_i|p_0 - q_0 + \epsilon p_0|\\ & \leqslant v^{0}_i(|p_0 - q_0| + \epsilon p_0) \\ & \leqslant v^{0}_i(v^{0}_i + 1)\epsilon. \end{align*}
\begin{align*} |p_i-q_i| & = v^{0}_i|p_0 - q_0 + \epsilon p_0|\\ & \leqslant v^{0}_i(|p_0 - q_0| + \epsilon p_0) \\ & \leqslant v^{0}_i(v^{0}_i + 1)\epsilon. \end{align*}Therefore, we conclude that
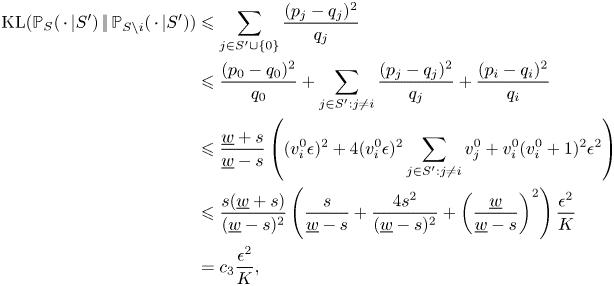 \begin{align*} {\textrm{KL}}({{\mathbb{P}}}_S(\,\cdot\,|S')\,|\!|\,{{\mathbb{P}}}_{S\backslash i}(\,\cdot\,|S')) & \leqslant \sum_{j\in S'\cup\{0\}} \frac{(p_j-q_j)^{2}}{q_j}\\ & \leqslant \frac{(p_0-q_0)^{2}}{q_0} + \sum_{j\in S':j\neq i} \frac{(p_j-q_j)^{2}}{q_j} + \frac{(p_i-q_i)^{2}}{q_i}\\ & \leqslant \frac{\underline{w}+s}{\underline{w}-s} \left((v_i^{0}\epsilon)^{2} + 4(v^{0}_i\epsilon)^{2}\sum_{j\in S':j\neq i}v_j^{0} + v_i^{0}(v_i^{0}+1)^{2} \epsilon^{2} \right)\\ & \leqslant \frac{s(\underline{w}+s)}{(\underline{w}-s)^{2}}\left(\frac{s}{\underline{w} -s } + \frac{4s^{2}}{(\underline{w}-s)^{2}} + \left(\frac{\underline{w}}{\underline{w}-s}\right)^{2}\right)\frac{\epsilon^{2}}{K}\\ & = c_3\frac{\epsilon^{2}}{K}, \end{align*}
\begin{align*} {\textrm{KL}}({{\mathbb{P}}}_S(\,\cdot\,|S')\,|\!|\,{{\mathbb{P}}}_{S\backslash i}(\,\cdot\,|S')) & \leqslant \sum_{j\in S'\cup\{0\}} \frac{(p_j-q_j)^{2}}{q_j}\\ & \leqslant \frac{(p_0-q_0)^{2}}{q_0} + \sum_{j\in S':j\neq i} \frac{(p_j-q_j)^{2}}{q_j} + \frac{(p_i-q_i)^{2}}{q_i}\\ & \leqslant \frac{\underline{w}+s}{\underline{w}-s} \left((v_i^{0}\epsilon)^{2} + 4(v^{0}_i\epsilon)^{2}\sum_{j\in S':j\neq i}v_j^{0} + v_i^{0}(v_i^{0}+1)^{2} \epsilon^{2} \right)\\ & \leqslant \frac{s(\underline{w}+s)}{(\underline{w}-s)^{2}}\left(\frac{s}{\underline{w} -s } + \frac{4s^{2}}{(\underline{w}-s)^{2}} + \left(\frac{\underline{w}}{\underline{w}-s}\right)^{2}\right)\frac{\epsilon^{2}}{K}\\ & = c_3\frac{\epsilon^{2}}{K}, \end{align*}where
Next, note that the entire probability measures ![]() ${{\mathbb {P}}}_S$ and
${{\mathbb {P}}}_S$ and ![]() ${{\mathbb {P}}}_{S\backslash i}$ depend on
${{\mathbb {P}}}_{S\backslash i}$ depend on ![]() $T$. Then, as a consequence of the chain rule of the KL divergence, we find that
$T$. Then, as a consequence of the chain rule of the KL divergence, we find that
Now, statement (3.8) follows from
 \begin{align} |\mathbb{E}_S [N_i] - \mathbb{E}_{S\backslash i} [N_i]|& \leqslant \sum_{n=0}^{T} n |{{\mathbb{P}}}_S(N_i=n) - {{\mathbb{P}}}_{S\backslash i} (N_i=n)| \nonumber\\ & \leqslant T\sum_{n=0}^{T} |{{\mathbb{P}}}_S(N_i=n) - {{\mathbb{P}}}_{S\backslash i} (N_i=n)| \nonumber\\ & = 2T\max_{n=0,\ldots,T}|{{\mathbb{P}}}_S(N_i=n) - {{\mathbb{P}}}_{S\backslash i} (N_i=n)| \nonumber\\ & \leqslant 2T\sup_{A} |{{\mathbb{P}}}_S(A) - {{\mathbb{P}}}_{S\backslash i} (A)| \nonumber\\ & \leqslant T\sqrt{2\,{\textrm{KL}}({{\mathbb{P}}}_S \,|\!|\,{{\mathbb{P}}}_{S\backslash i})}, \end{align}
\begin{align} |\mathbb{E}_S [N_i] - \mathbb{E}_{S\backslash i} [N_i]|& \leqslant \sum_{n=0}^{T} n |{{\mathbb{P}}}_S(N_i=n) - {{\mathbb{P}}}_{S\backslash i} (N_i=n)| \nonumber\\ & \leqslant T\sum_{n=0}^{T} |{{\mathbb{P}}}_S(N_i=n) - {{\mathbb{P}}}_{S\backslash i} (N_i=n)| \nonumber\\ & = 2T\max_{n=0,\ldots,T}|{{\mathbb{P}}}_S(N_i=n) - {{\mathbb{P}}}_{S\backslash i} (N_i=n)| \nonumber\\ & \leqslant 2T\sup_{A} |{{\mathbb{P}}}_S(A) - {{\mathbb{P}}}_{S\backslash i} (A)| \nonumber\\ & \leqslant T\sqrt{2\,{\textrm{KL}}({{\mathbb{P}}}_S \,|\!|\,{{\mathbb{P}}}_{S\backslash i})}, \end{align}where the step in (3.9) follows from, for example, Proposition 4.2 from Levin et al. [Reference Levin, Peres and Wilmer8] and we used Pinsker's inequality at the final inequality.
3.5. Step 4: Proving the main result
With all the established ingredients, we can finalize the proof of the lower bound on the regret.
Proof of Theorem 1. Since ![]() $v^{S}\in \mathcal {V}$ for all
$v^{S}\in \mathcal {V}$ for all ![]() $S\in \mathcal {S}_K$ and by Lemma 1, we know that
$S\in \mathcal {S}_K$ and by Lemma 1, we know that
 \begin{align} \Delta_{\pi}(T) & \geqslant \frac{1}{|\mathcal{S}_K|} \sum_{S \in \mathcal{S}_K} \Delta_{\pi}(T,v^{S}) \nonumber\\ & \geqslant c_2\,\epsilon \left(\vphantom{\sum_{S \in \mathcal{S}_K}}\right. T - \underbrace{\frac{1}{|\mathcal{S}_K|} \sum_{S \in \mathcal{S}_K} \frac{1}{K} \sum_{i \in S} \mathbb{E}_S [N_i]}_{(a)}\left.\vphantom{\sum_{S \in \mathcal{S}_K}}\right). \end{align}
\begin{align} \Delta_{\pi}(T) & \geqslant \frac{1}{|\mathcal{S}_K|} \sum_{S \in \mathcal{S}_K} \Delta_{\pi}(T,v^{S}) \nonumber\\ & \geqslant c_2\,\epsilon \left(\vphantom{\sum_{S \in \mathcal{S}_K}}\right. T - \underbrace{\frac{1}{|\mathcal{S}_K|} \sum_{S \in \mathcal{S}_K} \frac{1}{K} \sum_{i \in S} \mathbb{E}_S [N_i]}_{(a)}\left.\vphantom{\sum_{S \in \mathcal{S}_K}}\right). \end{align}We decompose ![]() $(a)$ into two terms:
$(a)$ into two terms:
 $$(a) = \underbrace{\frac{1}{|\mathcal{S}_K|} \sum_{S \in \mathcal{S}_K} \frac{1}{K} \sum_{i \in S} \mathbb{E}_{S \backslash i} [N_i] }_{(b)} + \underbrace{\frac{1}{|\mathcal{S}_K|} \sum_{S \in \mathcal{S}_K} \frac{1}{K} \sum_{i \in S} ( \mathbb{E}_{S} [N_i] - \mathbb{E}_{S \backslash i} [N_i] ) }_{(c)}.$$
$$(a) = \underbrace{\frac{1}{|\mathcal{S}_K|} \sum_{S \in \mathcal{S}_K} \frac{1}{K} \sum_{i \in S} \mathbb{E}_{S \backslash i} [N_i] }_{(b)} + \underbrace{\frac{1}{|\mathcal{S}_K|} \sum_{S \in \mathcal{S}_K} \frac{1}{K} \sum_{i \in S} ( \mathbb{E}_{S} [N_i] - \mathbb{E}_{S \backslash i} [N_i] ) }_{(c)}.$$Recall that ![]() $c = K/N\in (0,1/2)$. By summing over
$c = K/N\in (0,1/2)$. By summing over ![]() $S' = S \backslash i$ instead of over
$S' = S \backslash i$ instead of over ![]() $S$, we bound
$S$, we bound ![]() $(b)$ from above by
$(b)$ from above by
 $$(b) = \frac{1}{|\mathcal{S}_K|} \sum_{S' \in \mathcal{S}_{K-1}} \frac{1}{K} \sum_{i \notin S'} \mathbb{E}_{S'} [N_i] \leqslant \frac{|\mathcal{S}_{K-1}|}{|\mathcal{S}_K|} T \leqslant \frac{c}{1-c} T,$$
$$(b) = \frac{1}{|\mathcal{S}_K|} \sum_{S' \in \mathcal{S}_{K-1}} \frac{1}{K} \sum_{i \notin S'} \mathbb{E}_{S'} [N_i] \leqslant \frac{|\mathcal{S}_{K-1}|}{|\mathcal{S}_K|} T \leqslant \frac{c}{1-c} T,$$where the first inequality follows from ![]() $\sum _{i \in [N]} \mathbb {E}_{S' }[N_i] \leqslant T K$, and the second inequality from
$\sum _{i \in [N]} \mathbb {E}_{S' }[N_i] \leqslant T K$, and the second inequality from
 $$\frac{ |\mathcal{S}_{K-1}| }{ |\mathcal{S}_K|} = \frac{\binom{N}{K-1} }{ \binom{N}{K} } = \frac{K}{ N-K+1} \leqslant \frac{ K/N}{1 - K/N}.$$
$$\frac{ |\mathcal{S}_{K-1}| }{ |\mathcal{S}_K|} = \frac{\binom{N}{K-1} }{ \binom{N}{K} } = \frac{K}{ N-K+1} \leqslant \frac{ K/N}{1 - K/N}.$$Now, ![]() $(c)$ can be bounded by applying Lemma 2:
$(c)$ can be bounded by applying Lemma 2:
By plugging the upper bounds on ![]() $(b)$ and
$(b)$ and ![]() $(c)$ in (3.10), we obtain
$(c)$ in (3.10), we obtain
 \begin{align*} \Delta_{\pi}(T) & \geqslant c_2\epsilon \left( T - \frac{c}{1 - c} T - \frac{\sqrt{2c_3}}{\sqrt{c}} \frac{\epsilon T^{3/2}}{\sqrt{N}} \right)\\ & = c_2 \epsilon \left( \frac{1-2c}{1 - c} T - \frac{\sqrt{2c_3}}{\sqrt{c}} \frac{\epsilon T^{3/2}}{\sqrt{N}} \right). \end{align*}
\begin{align*} \Delta_{\pi}(T) & \geqslant c_2\epsilon \left( T - \frac{c}{1 - c} T - \frac{\sqrt{2c_3}}{\sqrt{c}} \frac{\epsilon T^{3/2}}{\sqrt{N}} \right)\\ & = c_2 \epsilon \left( \frac{1-2c}{1 - c} T - \frac{\sqrt{2c_3}}{\sqrt{c}} \frac{\epsilon T^{3/2}}{\sqrt{N}} \right). \end{align*}Now, we set ![]() $\epsilon$ as
$\epsilon$ as
This yields, for all ![]() $T \geqslant N$,
$T \geqslant N$,
Finally, note that for ![]() $T\geqslant N$ it follows that
$T\geqslant N$ it follows that ![]() $T\geqslant \sqrt {NT}$ and therefore
$T\geqslant \sqrt {NT}$ and therefore
where
Acknowledgments
The authors thank the Editor in Chief and an anonymous reviewer for their positive remarks and useful comments.
Competing interest
The authors declare no conflict of interest.