No CrossRef data available.
Article contents
RATIO MONOTONICITY FOR TAIL PROBABILITIES IN THE RENEWAL RISK MODEL
Published online by Cambridge University Press: 31 March 2011
Abstract
A renewal model in risk theory is considered, where 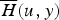 is the tail of the distribution of the deficit at ruin with initial surplus u and
is the tail of the distribution of the deficit at ruin with initial surplus u and 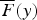 is the tail of the ladder height distribution. Conditions are derived under which the ratio
is the tail of the ladder height distribution. Conditions are derived under which the ratio  is nondecreasing in u for any y≥0. In particular, it is proven that if the ladder height distribution is stable and DFR or phase type, then the above ratio is nondecreasing in u. As a byproduct of this monotonicity, an upper bound and an asymptotic result for
is nondecreasing in u for any y≥0. In particular, it is proven that if the ladder height distribution is stable and DFR or phase type, then the above ratio is nondecreasing in u. As a byproduct of this monotonicity, an upper bound and an asymptotic result for  are derived. Examples are given to illustrate the monotonicity results.
are derived. Examples are given to illustrate the monotonicity results.
- Type
- Research Article
- Information
- Probability in the Engineering and Informational Sciences , Volume 25 , Issue 2 , April 2011 , pp. 171 - 185
- Copyright
- Copyright © Cambridge University Press 2011


