Article contents
RANDOM FINITE SUBSETS WITH EXPONENTIAL DISTRIBUTIONS
Published online by Cambridge University Press: 15 December 2006
Abstract
Let S denote the collection of all finite subsets of
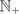 .
We define an operation on S that makes S into a
positive semigroup with set inclusion as the associated partial order.
Positive semigroups are the natural home for probability distributions
with exponential properties, such as the memoryless and constant rate
properties. We show that there are no exponential distributions on
S, but that S can be partitioned into subsemigroups,
each of which supports a one-parameter family of exponential
distributions. We then find the distribution on S that is closest
to exponential, in a certain sense. This work might have applications to
the problem of selecting a finite sample from a countably infinite
population in the most random way.
.
We define an operation on S that makes S into a
positive semigroup with set inclusion as the associated partial order.
Positive semigroups are the natural home for probability distributions
with exponential properties, such as the memoryless and constant rate
properties. We show that there are no exponential distributions on
S, but that S can be partitioned into subsemigroups,
each of which supports a one-parameter family of exponential
distributions. We then find the distribution on S that is closest
to exponential, in a certain sense. This work might have applications to
the problem of selecting a finite sample from a countably infinite
population in the most random way.
- Type
- Research Article
- Information
- Probability in the Engineering and Informational Sciences , Volume 21 , Issue 1 , January 2007 , pp. 117 - 132
- Copyright
- © 2007 Cambridge University Press
References
REFERENCES
- 1
- Cited by


