Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-04T21:19:51.365Z Has data issue: false hasContentIssue false
  • English
  • Français

ORDER STATISTICS FROM DEPENDENT, COMPLETELY MONOTONE DISTRIBUTIONS

Published online by Cambridge University Press:  30 April 2009

Mark Brown
Mark Brown
Affiliation:
Department of Mathematics, The City College, CUNY, New York, NY 10031 E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider order statistics corresponding to X1, …, Xn, where 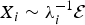, i = 1, …, n, ℰ1, …, ℰn are independent and identically distributed exponentials with mean 1, and λ1, …, λn are possibly dependent, possibly nonidentically distributed, positive random variables, with 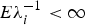. Thus, λ1, …, λn, can be interpreted as random failure rates, and their dependency might be due to common environmental factors.

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 23 , Issue 3 , July 2009 , pp. 449 - 455
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Barlow, R.E., Bartholomew, D.J., Bremner, J.M. & Brunk, H.D. (1972). Statistical inference under order restrictions. New York: Wiley.Google Scholar
2.Brown, M. (2006). Exploiting the waiting time paradox: Applications of the size-biasing transformation. Probability in the Engineering and Informationa Sciences 20: 195–230.CrossRefGoogle Scholar
3.Marshall, A.W. & Olkin, I. (2007). Life distributions, structure of nonparametric, semiparametric, and parametric families. New York: Springer.Google Scholar
4.Olkin, I. & Shepp, L. (2006). Several colorful inequalities. The American Mathematical Monthly 113: 817–822.CrossRefGoogle Scholar
5.Ross, S.M. (2007). Introduction to probability models, 9th ed.Amsterdam: Elsevier.Google Scholar