Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-22T14:30:01.526Z Has data issue: false hasContentIssue false
  • English
  • Français

ON DETERMINISTIC FINITE STATE MACHINES IN RANDOM ENVIRONMENTS

Published online by Cambridge University Press:  05 December 2018

Joel Ratsaby
Joel Ratsaby*
Affiliation:
Electrical and Electronics Engineering Department, Ariel University, Ariel 40700, Israel E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The general problem under investigation is to understand how the complexity of a system which has been adapted to its random environment affects the level of randomness of its output (which is a function of its random input). In this paper, we consider a specific instance of this problem in which a deterministic finite-state decision system operates in a random environment that is modeled by a binary Markov chain. The system interacts with it by trying to match states of inactivity (represented by 0). Matching means that the system selects the (t + 1)th bit from the Markov chain whenever it predicts at time t that the environment will take a 0 value. The actual value at time t + 1 may be 0 or 1 thus the selected sequence of bits (which forms the system's output) may have both binary values. To try to predict well, the system's decision function is inferred based on a sample of the random environment.

We are interested in assessing how non-random the output sequence may be. To do that, we apply the adapted system on a second random sample of the environment and derive an upper bound on the deviation between the average number of 1 bit in the output sequence and the probability of a 1. The bound shows that the complexity of the system has a direct effect on this deviation and hence on how non-random the output sequence may be. The bound takes the form of 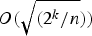$O(\sqrt {(2^k/n} ))$ where 2k is the complexity of the system and n is the length of the second sample.

Keywords

prediction of random binary sequenceMarkov chainsubsequence selectionfrequency instability
Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 33 , Issue 4 , October 2019 , pp. 528 - 563
Copyright
Copyright © Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Asarin, A.E. (1988). On some properties of finite objects random in an algorithmic sense. Soviet Mathematics Doklady 36(1): 109–112.Google Scholar
2.Bartlett, P.L. (1998). The sample complexity of pattern classification with neural networks: the size of the weights is more important than the size of the network. IEEE Transactions on Information Theory 44(2): 525–536.Google Scholar
3.Behrends, E. (2000). Introduction to Markov Chains: With Special Emphasis on Rapid Mixing. Advanced Lectures in Mathematics. Wiesbaden, Germany: Springer Fachmedien Wiesbaden.Google Scholar
4.Bienvenu, L. (2007). Kolmogorov-Loveland stochasticity and Kolmogorov complexity. In Proc. of 24th Annual Symposium on Theoretical Aspects of Computer Science (STACS 2007), volume LNCS 4393, 260–271.Google Scholar
5.Bressloff, P.C. (2014). Stochastic processes in cell biology. International Publishing, Switzerland: Springer.Google Scholar
6.Chernoff, H. (1952). A measure of asymptotic efficiency for tests of a hypothesis based on the sum of observations. Annals of Mathematical Statistics 23, 493–507.Google Scholar
7.Chow, C.K. (1957). An optimum character recognition system using decision functions. Electronic Computers, IRE Transactions on EC-6(4): 247–254.Google Scholar
8.Falin, G. (1996). A heterogeneous blocking system in a random environment. Journal of Applied Probability 33(1): 211–216.Google Scholar
9.Kolmogorov, A.N. (1998). On tables of random numbers. Theoretical Computer Science 207(2): 387–395.Google Scholar
10.Kontorovich, A. & Weiss, R. (2014). Uniform Chernoff and Dvoretzky-Kiefer-Wolfowitz-type inequalities for Markov chains and related processes. Journal of Applied Probability 51(4): 1100–1113.Google Scholar
11.Merhav, N. & Feder, M. (1998). Universal prediction. IEEE Transactions on Information Theory 44(6): 2124–2147.Google Scholar
12.Meyer, C.D. (ed.) (2000). Matrix Analysis and Applied Linear Algebra. Philadelphia, PA, USA: Society for Industrial and Applied Mathematics.Google Scholar
13.Najim, K. & Poznyak, A.S. (1994). Learning automata: theory and applications. Elmsford, NY, USA: Pergamon Press Inc.Google Scholar
14.Nicolas, P. (2013). Understanding Markov chains, examples and applications. Singapore: Springer.Google Scholar
15.Petakos, K. & Tsapelas, T. (1997). Reliability analysis for systems in a random environment. Journal of Applied Probability 34(4): 1021–1031.Google Scholar
16.Ratsaby, J. (2008). An algorithmic complexity interpretation of Lin's third law of information theory. Entropy 10(1): 6–14.Google Scholar
17.Ratsaby, J. (2011). An empirical study of the complexity and randomness of prediction error sequences. Communications in Nonlinear Science and Numerical Simulation 16, 2832–2844.Google Scholar
18.Ratsaby, J. (2011). On the sysratio and its critical point. Mathematical and Computer Modelling 53, 939–944.Google Scholar
19.White, B.S. (1977). The effects of a rapidly-fluctuating random environment on systems of interacting species. SIAM Journal on Applied Mathematics 32(3): 666–693.Google Scholar
20.Wijker, J.J. (2009). Random vibrations in spacecraft structures design, theory and applications. Dordrecht, Netherlands: Springer.Google Scholar
21.Wortman, M.A. & Klutke, G.A. (1994). On maintained systems operating in a random environment. Journal of Applied Probability 31(2): 589–594.Google Scholar