1. Introduction
Square-root diffusion has become a popular model in the econometric area since it was first proposed by [Reference Cox, Ingersoll and Ross12] for modeling the term structure of interest rates, thus it is also called Cox–Ingersoll–Ross (CIR) model. Heston [Reference Heston17] further extends its usage in option pricing by using it in modeling the underling asset price volatility, to improve the famous Black–Scholes option pricing formula. Among an important class of processes, affine jump-diffusions (see [Reference Duffie, Pan and Singleton14]), square-root diffusion functions as a major component. One-factor square-root diffusion is preferred for simple cases, however, superposition of several square-root diffusions or multi-factor square-root diffusion plays a more important role in many applications because of its better explanation for many scenarios in practice. Barndorff-Nielsen [Reference Barndorff-Nielsen5] constructs a class of stochastic processes based on the superposition of Ornstein–Uhlenbeck type processes. In this paper we consider the problem of parameter estimation for superposition of square-root diffusions.
Due to lack of closed-form transition density, maximum likelihood estimation (MLE) is not applicable to the problem of our interest without approximation. Even for one-factor square-root diffusion, this remains the case, though the transition law is known as a scaled noncentral chi-square distribution (see [Reference Cox, Ingersoll and Ross12]). What is worse is the log likelihood is not globally concave, as pointed out in [Reference Overbeck and Rydén22] for the one-factor model, which makes the efficiency of MLE depending on the goodness of starting values in numerical optimization algorithms. Therefore, Overbeck and Rydén [Reference Overbeck and Rydén22] propose conditional least-squares estimators for the parameters of the one-factor model. Almost all the previous works on the parameter estimation for the superposition of square-root diffusions are based on various types of approximations. By using a closed-form approximation of the density, Ait-Sahalia and Kimmel [Reference Ait-Sahalia and Kimmel1] design an MLE for the multi-factor model, in which they first make the factors (states) observable by inverting the zero-coupon bond yields. This simplification makes it not applicable to general cases where the states are latent, such as the superposition of square-root diffusions studied in this paper. Using Kalman filter is another way of approximation. By approximating the transition density with a normal density, Geyer and Pichler [Reference Geyer and Pichler16] first infer the unobservable states with an approximate Kalman filter, and then estimate the parameters with quasi-maximum-likelihood estimation; see [Reference Chen and Scott9] for another Kalman filter approach. Christoffersen et al. [Reference Christoffersen, Dorion, Jacobs and Karoui10] consider nonlinear Kalman filtering of multi-factor affine term structure models. Based on continuous time observations, Barczy et al. [Reference Barczy, Do, Li and Pap4] estimate the parameters by MLE and least squares of a subcritical affine two-factor model in which one factor is a square-root diffusion. There are some works that only consider the drift-parameter estimation for the one-factor model, such as [Reference Alaya and Kebaier2], [Reference Dehtiar, Mishura and Ralchenko13], and parameter estimation for extended one-dimensional CIR model, such as [Reference Barczy, Alaya, Kebaier and Pap3], [Reference Li and Ma20], [Reference Cleur11], and [Reference Mishura, Ralchenko and Dehtiar21]. A gradient-based simulated MLE estimate is proposed in [Reference Peng, Fu and Hu23, Reference Peng, Fu and Hu24] for a related model. In summary, these approximations used in the MLE methods are computationally time-consuming, and some of the assumptions may be hard to satisfy in practical applications.
Method of moments (MM) offers an alternative to likelihood-based estimation, especially for cases where the likelihood does not have a closed-form expression while the moments can be easily derived analytically, see [Reference Van der Vaart26] and [Reference Casella and Berger8] for detailed description. The major issue of moment-based methods is the so-called statistical inefficiency in the sense that the higher order moments are used, the greater likelihood of estimation bias occurs. However, it is possible to overcome this problem by making use of relative low order moments and employing better computational techniques, for example, see [Reference Wu, Hu and Yang27–Reference Yang, Wu, Zheng and Hu30].
In this paper, we consider the superposition of square-root diffusions and develop explicit MM estimators for the parameters in such a model. We first derive the closed-form formulas for the moments and auto-covariances, and then use them to develop our MM estimators. In fact, we only need relatively low order moments and auto-covariances. We also prove the central limit theorem for our MM estimators and derive the explicit formulas for the asymptotic covariance matrix. Additionally, numerical experiments are conducted to test the efficiency of our method. One clear advantage of our estimators is their simplicity and ease of implementation.
The rest of the paper is organized as follows. In Section 2, we present the model for the superposition of square-root diffusions and calculate the moments and auto-covariances. In Section 3, we derive our MM estimators and establish the central limit theorem. In Section 4, we provide some numerical experiments. Section 5 concludes this paper. The appendix contains some of the detailed calculations omitted in the main body of the paper.
2. Preliminaries
For ease of exposition, we focus on the superposition of two square-root diffusions which is usually used in most applications. The basic of our method can be extended to cases with multiple square-root diffusions, though as the number of square-root diffusions increases, calculations become more tedious and complex. The two-factor square-root diffusion can be described by the following stochastic differential equations:
\begin{align}
x(t) &= x_1(t) + x_2(t),
\end{align}
\begin{align}
dx_1(t) &= k_1(\theta_1 - x_1(t))dt + \sigma_{x1}\sqrt{x_1(t)}dw_1(t),
\end{align}
\begin{align}
dx_2(t) &= k_2(\theta_2 - x_2(t))dt + \sigma_{x2}\sqrt{x_2(t)}dw_2(t),
\end{align} where the two square-root diffusions (also called CIR processes) 
$x_1(t)$ and 
$x_2(t)$ are independent of each other, 
$w_1(t)$ and 
$w_2(t)$ are two Wiener processes with independent initial values 
$x_1(0) \gt 0$ and 
$x_2(0) \gt 0$, respectively. The parameters 
$k_i \gt 0,\theta_i \gt 0,\sigma_{xi} \gt 0$ satisfy the condition 
$\sigma_{xi}^2 \le 2k_i\theta_i$ for 
$i=1,2$, which assures 
$x_i(t) \gt 0$ for t > 0 (see [Reference Cox, Ingersoll and Ross12]). The component processes 
$x_1(t)$, 
$x_2(t)$ and the driving processes 
$w_1(t)$, 
$w_2(t)$ are all latent, except that x(t) is observable.
The square-root diffusions in Eqs. (2.2) and (2.3) can be re-written as:
\begin{equation}
x_i(t) = e^{-k_i(t-s)}x_i(s) + \theta_i \left[1- e^{-k_i(t-s)}\right] + \sigma_{xi}e^{-k_it}\int_s^te^{k_iu}\sqrt{x_i(u)}dw_i(u),
\end{equation} for 
$i=1,2$. The process 
$x_i(t)$ decays at an exponential rate 
$e^{-k_it}$, thus the parameter ki is called the decay parameter. It is easy to see that 
$x_i(t)$ has a long-run mean θi and its instantaneous volatility is determined by its current value and σxi. In fact, the process 
$x_i(t)$ is a Markov process and has a steady-state gamma distribution with mean θi and variance 
$\theta_i\sigma_{xi}^2/(2k_i)$ (see [Reference Cox, Ingersoll and Ross12]). Since we are interested in estimating the parameters based on a larger number of samples of the process, without loss of generality, throughout this paper it is assumed that 
$x_i(0)$ is distributed according to the steady-state distribution of 
$x_i(t)$, implying that 
$x_i(t)$ is strictly stationary and ergodic (see [Reference Overbeck and Rydén22]). Therefore, the process x(t) is also strictly stationary and ergodic. Actually, all the results we shall derive in the rest of this paper remain the same for any non-negative 
$x_1(0)$ and 
$x_2(0)$ as long as the observation time t is sufficiently long. Since 
$x_i(t)$ is stationary, it has a gamma distribution with mean θi and variance 
$\theta_i\sigma_{xi}^2/(2k_i)$ and its mth moment is given by
\begin{equation}
E[x_i^{m}(t)] = \prod_{j=0}^{m-1}\left(\theta_i + \frac{j\sigma_{xi}^2}{2k_i}\right),\quad m=1,2,\ldots.
\end{equation} Though modeled as a continuous time process, x(t) is actually observed at discrete time points. Assume x(t) is observed at equidistant time points 
$t=nh, n=0,1,\ldots,N$ and let 
$x_n \triangleq x(nh)$. Similarly, let 
$x_{in} \triangleq x_i(nh)$. We denote the mth central moment of xn by 
${\rm cm}_m[x_n]$, that is, 
${\rm cm}_m[x_n] \triangleq E[(x_n - E[x_n])^m]$. Then, we have
\begin{equation}
{\rm cm}_m[x_n] = \sum_{j=0}^m C_m^{j} E[(x_{1n}-\theta_1)^{j}]E[(x_{2n}-\theta_2)^{m-j}],
\end{equation} due to the independence between 
$x_{1n}$ and 
$x_{2n}$, where 
$C_m^{j}$ is the combinatorial number. For notation simplicity, we introduce 
$\sigma_1 \triangleq \sigma_{x1}^2/(2k_1)$ and 
$\sigma_2 \triangleq \sigma_{x2}^2/(2k_2)$.
With Eqs. (2.4)–(2.6), we have the following moment and auto-covariance formulas
\begin{align}
E[x_n] &= \theta_1 + \theta_2,
\end{align}
\begin{align}
{\rm var}(x_n) &= \theta_1\sigma_1 + \theta_2\sigma_2,
\end{align}
\begin{align}
{\rm cm}_3[x_n] &= 2\theta_1\sigma_1^2 + 2\theta_2\sigma_2^2,
\end{align}
\begin{align}
{\rm cov}(x_n,x_{n+1}) &= e^{-k_1h}\theta_1\sigma_1 + e^{-k_2h}\theta_2\sigma_2,
\end{align}
\begin{align}
{\rm cov}(x_n,x_{n+2}) &= e^{-2k_1h}\theta_1\sigma_1 + e^{-2k_2h}\theta_2\sigma_2,
\end{align}
\begin{align}
{\rm cov}(x_n,x_{n+3}) &= e^{-3k_1h}\theta_1\sigma_1 + e^{-3k_2h}\theta_2\sigma_2.
\end{align}The intermediate steps of the derivation are omitted because they are straightforward. We will use these six moments/auto-covariances to construct our estimators of the parameters in the next section.
3. Parameter estimation
In this section, we derive our MM estimators for the six parameters in Eqs. (2.2) and (2.3) based on the moments/auto-covariances obtained in the previous section. We prove both the moment/auto-covariance estimators and the MM estimators satisfy the central limit theorem and also compute the explicit formulas for their asymptotic covariance matrices.
Assume that we are given a sample path of x(t), 
$X_1, \ldots, X_N$, that is, samples of the stochastic process x(t) observed at 
$t = h, \ldots, Nh$, which will be used to calculate the sample moments and auto-covariances of xn as the estimates for their population counterparts:
\begin{align*}
E[x_n] &\approx \overline{X} \triangleq \frac{1}{N}\sum_{n=1}^N X_n,\\
{\rm var}(x_n) &\approx S^2 \triangleq \frac{1}{N}\sum_{n=1}^N(X_n - \overline{X})^2,\\
{\rm cm}_3[x_n] &\approx \hat{{\rm cm}}_3[x_n] \triangleq \frac{1}{N}\sum_{n=1}^{N}(X_n - \overline{X})^3,\\
{\rm cov}(x_n,x_{n+1}) &\approx \hat{{\rm cov}}(x_n,x_{n+1}) \triangleq \frac{1}{N-1}\sum_{n=1}^{N-1}(X_n-\overline{X})(X_{n+1}-\overline{X}),\\
{\rm cov}(x_n,x_{n+2}) &\approx \hat{{\rm cov}}(x_n,x_{n+2}) \triangleq \frac{1}{N-2}\sum_{n=1}^{N-2}(X_n-\overline{X})(X_{n+2}-\overline{X}),\\
{\rm cov}(x_n,x_{n+3}) &\approx \hat{{\rm cov}}(x_n,x_{n+3}) \triangleq \frac{1}{N-3}\sum_{n=1}^{N-3}(X_n-\overline{X})(X_{n+3}-\overline{X}).
\end{align*}Let
\begin{align*}
\boldsymbol{\gamma} &= (E[x_n],{\rm var}(x_n),{\rm cm}_3[x_n],{\rm cov}(x_n,x_{n+1}),{\rm cov}(x_n,x_{n+2}),{\rm cov}(x_n,x_{n+3}))^T,\\
\hat{\boldsymbol{\gamma}} &= (\overline{X},S^2,\hat{{\rm cm}}_3[x_n],\hat{{\rm cov}}(x_n,x_{n+1}),\hat{{\rm cov}}(x_n,x_{n+2}),\hat{{\rm cov}}(x_n,x_{n+3}))^T,
\end{align*}where T denotes the transpose of a vector or matrix. We also define
\begin{align*}
z^1_n &\triangleq (x_n-E[x_n])^2, &z^2_n &\triangleq (x_n-E[x_n])^3, \\
z^3_n &\triangleq (x_n-E[x_n])(x_{n+1}-E[x_n]), &z^4_n &\triangleq (x_n-E[x_n])(x_{n+2}-E[x_n]), \\
z^5_n &\triangleq (x_n-E[x_n])(x_{n+3}-E[x_n]),& z_n&\triangleq (z_n^1,z_n^2,z_n^3,z_n^4,z_n^5).
\end{align*}Let
\begin{align*}
\sigma_{11}
&= \lim_{N\rightarrow\infty}\frac{1}{N}\boldsymbol{1}_N^T[{\rm cov}(x_r,x_c)]_{N\times N}\boldsymbol{1}_N, \\
\sigma_{1m}
&= \lim_{N\rightarrow\infty}\frac{1}{N}\boldsymbol{1}_N^T[{\rm cov}(x_r,z_c^{m-1})]_{N\times N_m}\boldsymbol{1}_{N_m}, \qquad 2\le m \le 6,\\
\sigma_{lm}
&= \lim_{N\rightarrow\infty}\frac{1}{N}\boldsymbol{1}_{N_l}^T[{\rm cov}(z_r^{l-1}, z_c^{m-1})]_{N_l\times N_m}\boldsymbol{1}_{N_m},\quad 2\le l\le m \le 6,
\end{align*} where 
$(N_2,N_3,N_4,N_5,N_6) = (N,N,N-1,N-2,N-3)$ and 
$\boldsymbol{1}_p = (1,\cdots,1)^T$ with p elements. We further introduce the following notations:
\begin{align*}
e_{ij}&\triangleq \frac{e^{-jk_ih}}{1-e^{-jk_ih}},\qquad\quad i=1,2, j=1,2,\ldots,\\
e_{p,q}&\triangleq \frac{e^{-(pk_1+qk_2)h}}{1-e^{-(pk_1+qk_2)h}},\quad p=0,1,\cdots, q= 0,1,\ldots,
\end{align*} and 
$\bar{x}_{1n}\triangleq x_{1n} - \theta_1$ and 
$\bar{x}_{2n}\triangleq x_{2n} - \theta_2$. We are now ready to prove the following central limit theorem for our moment/auto-covariance estimators.
\begin{equation}
\lim_{N\rightarrow\infty}\sqrt{N}(\hat{\boldsymbol{\gamma}} - \boldsymbol{\gamma}) \overset{d}{=} \mathcal{N}(\boldsymbol{0},\Sigma),
\end{equation} where 
$\overset{d}{=}$ denotes equal in distribution and 
$\mathcal{N}(\boldsymbol{0},\Sigma)$ is a multivariate normal distribution with mean 0 and asymptotic covariance matrix 
$\Sigma = [\sigma_{lm}]_{6\times 6}$, with entries
\begin{equation*}\sigma_{lm}= c_{lm,1} + c_{lm,2}, \quad l,m=1,\ldots,6,\end{equation*} where 
$c_{lm,1}$, 
$c_{lm,2}$ are some constants which are provided in the Appendix.
Proof. The square-root diffusion 
$x_{i}(t)$ (
$i=1,2$) is a Markov process, so is the discrete-time process xin. 
$\{(x_{1n},x_{2n},x_{n})\}$ is also a Markov process. Under the condition 
$\sigma_{xi}^2\le 2k_i\theta_i$, the strictly stationary square-root diffusion 
$x_i(t)$ is ρ-mixing; see Proposition 2.8 in [Reference Genon-Catalot, Jeantheau and Larédo15]. Hence, 
$x_{i}(t)$ is ergodic and strong mixing (also known as α-mixing) with an exponential rate; see [Reference Bradley6]. The discrete-time process 
$\{x_{in}\}$ is also ergodic and inherits the exponentially fast strong mixing properties of 
$x_i(t)$. It can be verified that 
$\{(x_{1n},x_{2n},x_{n})\}$ is also ergodic and strong mixing with an exponential rate. Applying the central limit theorem for strictly stationary strong mixing sequences (see Theorem 1.7 in [Reference Ibragimov18]), we can prove Eq. (3.1) as Corollary 3.1 in [Reference Genon-Catalot, Jeantheau and Larédo15].
Next, we present the calculations for the diagonal entries of the asymptotic covariance matrix, however omit those for the off-diagonal entries since they are very similar. First, we point out the following formulas
\begin{equation*}
\sum_{1\le r \lt c \le N}e^{-(c-r)kh}
= \frac{e^{-kh}}{1-e^{-kh}}(N-1) - \frac{e^{-2kh - e^{-(N+1)kh}}}{(1-e^{-kh})^2},
\end{equation*}which will be used frequently to calculate infinite series in these entries. We now calculate the six diagonal entries.
• σ 11: We have
\begin{align*}
\sigma_{11}
&= \lim_{N\rightarrow\infty}\frac{1}{N}\left( N{\rm var}(x_n) + 2\sum_{1\le {r \lt c}\le N}{\rm cov}(x_r,x_c) \right)\\
&= {\rm var}(x_n) + 2\lim_{N\rightarrow\infty}\frac{1}{N}\sum_{1\le r \lt c\le N}({\rm cov}(x_{1r},x_{1c})+{\rm cov}(x_{2r},x_{2c}))\\
&= {\rm var}(x_{1n})+{\rm var}(x_{2n}) + \frac{2e^{-k_1h}}{1-e^{-k_1h}}{\rm var}(x_{1n}) + \frac{2e^{-k_2h}}{1-e^{-k_2h}}{\rm var}(x_{2n})\\
&= (1+2e_{11})\frac{\theta_1\sigma_{x1}^2}{2k_1} + (1+2e_{21})\frac{\theta_2\sigma_{x2}^2}{2k_2},
\end{align*}where we have used the results of
${\rm cov}(x_{1r},x_{1c}) = e^{-(c-r)k_1h}{\rm var}(x_{1r})$ (r < c), ${\rm var}(x_{1r}) = {\rm var}(x_{1n})$, $\forall r = 1,\cdots, N$ (similarly for $x_{2r}$).• σ 22: We have
\begin{align*}
\sigma_{22}
&= \lim_{N\rightarrow\infty}\frac{1}{N}\left( N{\rm var}(z_n^1) + 2\sum_{1\le r \lt c \le N}{\rm cov}(z_r^1,z_c^1) \right)\\
&={\rm var}(\bar{x}_{1n}^2) + {\rm var}(\bar{x}_{2n}^2) + 4{\rm var}(x_{1n}){\rm var}(x_{2n})\\
&\quad+\lim_{N\rightarrow\infty}\frac{2}{N}\sum_{1\le r \lt c \le N}({\rm cov}(\bar{x}_{1r}^2, \bar{x}_{1c}^2) + {\rm cov}(\bar{x}_{2r}^2, \bar{x}_{2c}^2) + 4{\rm cov}(\bar{x}_{1r}\bar{x}_{2r}, \bar{x}_{1c}\bar{x}_{2c}) )\\
&= c_{22,1} + c_{22,2},
\end{align*}where
${\rm cov}(\bar{x}_{1r}^2, \bar{x}_{1c}^2)$ (r < c) can be calculated as
\begin{align*}
&{\rm cov}(\bar{x}_{1r}^2, \bar{x}_{1c}^2)\\
&= e^{-2(c-r)k_1h}{\rm var}(\bar{x}_{1r}^2) + \frac{\sigma_{x1}^2}{k_1}[e^{-(c-r)k_1h} - e^{-2(c-r)k_1h}]{\rm cov}(\bar{x}_{1r}^2, \bar{x}_{1r}),
\end{align*}in which we have used the decay formula (A.2) for
$\bar{x}_{1c}^2$ in the Appendix, similarly for ${\rm cov}(\bar{x}_{2r}^2, \bar{x}_{2c}^2)$ (r < c), and ${\rm cov}(\bar{x}_{1r}\bar{x}_{2r}, \bar{x}_{1c}\bar{x}_{2c})$ (r < c) as
\begin{align*}
{\rm cov}(\bar{x}_{1r}\bar{x}_{2r}, \bar{x}_{1c}\bar{x}_{2c})
&= e^{-(c-r)(k_1+k_2)h}{\rm var}(x_{1r}){\rm var}(x_{2r}).
\end{align*}• σ 33: We have
\begin{align*}
\sigma_{33}
&= \lim_{N\rightarrow\infty}\frac{1}{N}\left( N{\rm var}(z_n^2) + 2\sum_{1\le r \lt c \le N}{\rm cov}(z_r^2,z_c^2)\right)\\
&= c_{33,1} + c_{33,2},
\end{align*}where
${\rm cov}(z_r^2,z_c^2)$ can be expanded as
\begin{align*}
{\rm cov}(z_r^2,z_c^2) &= ({\rm cov}(\bar{x}_{1r}^3,\bar{x}_{1c}^3) + {\rm cov}(\bar{x}_{2r}^3,\bar{x}_{2c}^3))
+ 3({\rm cov}(\bar{x}_{1r}^3, \bar{x}_{1c}\bar{x}_{2c}^2) + {\rm cov}(\bar{x}_{2r}^3,\bar{x}_{1c}^2\bar{x}_{2c}))\\
&\quad + 9({\rm cov}(\bar{x}_{1r}^2\bar{x}_{2r},\bar{x}_{1c}^2\bar{x}_{2c}) + {\rm cov}(\bar{x}_{1r}\bar{x}_{2r}^2,\bar{x}_{1c}\bar{x}_{2c}^2))\\
&\quad + 9({\rm cov}(\bar{x}_{1r}^2\bar{x}_{2r},\bar{x}_{1c}\bar{x}_{2c}^2) + {\rm cov}(\bar{x}_{1r}\bar{x}_{2r}^2,\bar{x}_{1c}^2\bar{x}_{2c}) )\\
&\quad + 3({\rm cov}(\bar{x}_{1r}^2\bar{x}_{2r},\bar{x}_{2c}^3) + {\rm cov}(\bar{x}_{1r}\bar{x}_{2r}^2,\bar{x}_{1c}^3)).
\end{align*}•
$\sigma_{44}:$ We have
\begin{align*}
\sigma_{44}
&= \lim_{N\rightarrow\infty}\frac{1}{N}\left[ (N-1){\rm var}(z_n^3) + 2\sum_{1\le r \lt c \le N-1}{\rm cov}(z_r^3,z_c^3)\right]\\
&= c_{44,1} + c_{44,2},
\end{align*}where
${\rm cov}(z_r^3,z_c^3)$ is expanded as
\begin{align*}
{\rm cov}(z_r^3,z_c^3)
&= ({\rm cov}(\bar{x}_{1r}\bar{x}_{1(r+1)},\bar{x}_{1c}\bar{x}_{1(c+1)}) + {\rm cov}(\bar{x}_{2r}\bar{x}_{2(r+1)},\bar{x}_{2c}\bar{x}_{2(c+1)}))\\
&\quad + ( {\rm cov}(\bar{x}_{1r}\bar{x}_{2(r+1)},\bar{x}_{1c}\bar{x}_{2(c+1)}) + {\rm cov}(\bar{x}_{2r}\bar{x}_{1(r+1)},\bar{x}_{2c}\bar{x}_{1(c+1)}) )\\
&\quad + ( {\rm cov}(\bar{x}_{1r}\bar{x}_{2(r+1)},\bar{x}_{2c}\bar{x}_{1(c+1)}) + {\rm cov}(\bar{x}_{2r}\bar{x}_{1(r+1)},\bar{x}_{1c}\bar{x}_{2(c+1)}) ).
\end{align*}•
$\sigma_{55}:$ We have
\begin{align*}
\sigma_{55}
&= \lim_{N\rightarrow\infty}\frac{1}{N}\left[ (N-2){\rm var}(z_n^4) + 2\sum_{1\le r \lt c \le N-2}{\rm cov}(z_r^4,z_c^4)\right]\\
&= c_{55,1} + c_{55,2},
\end{align*}where
${\rm cov}(z_r^4,z_{c}^4)$ can be calculated through
\begin{align*}
{\rm cov}(z_r^4,z_c^4)
&= ({\rm cov}(\bar{x}_{1r}\bar{x}_{1(r+2)},\bar{x}_{1c}\bar{x}_{1(c+2)}) + {\rm cov}(\bar{x}_{2r}\bar{x}_{2(r+2)},\bar{x}_{2c}\bar{x}_{2(c+2)}))\\
&\quad + ( {\rm cov}(\bar{x}_{1r}\bar{x}_{2(r+2)},\bar{x}_{1c}\bar{x}_{2(c+2)}) + {\rm cov}(\bar{x}_{2r}\bar{x}_{1(r+2)},\bar{x}_{2c}\bar{x}_{1(c+2)}) )\\
&\quad + ( {\rm cov}(\bar{x}_{1r}\bar{x}_{2(r+2)},\bar{x}_{2c}\bar{x}_{1(c+2)}) + {\rm cov}(\bar{x}_{2r}\bar{x}_{1(r+2)},\bar{x}_{1c}\bar{x}_{2(c+2)}) ).
\end{align*}•
$\sigma_{66}:$ We have
\begin{align*}
\sigma_{66}
&= \lim_{N\rightarrow\infty}\frac{1}{N}\left[ (N-3){\rm var}(z_n^5) + 2\sum_{1\le r \lt c \le N-3}{\rm cov}(z_r^5,z_c^5)\right]\\
&= c_{66,1} + c_{66,2},
\end{align*}where
${\rm cov}(z_r^5,z_{c}^5)$ can be calculated through
\begin{align*}
{\rm cov}(z_r^5,z_c^5)
&= ({\rm cov}(\bar{x}_{1r}\bar{x}_{1(r+3)},\bar{x}_{1c}\bar{x}_{1(c+3)}) + {\rm cov}(\bar{x}_{2r}\bar{x}_{2(r+3)},\bar{x}_{2c}\bar{x}_{2(c+3)}))\\
&\quad + ( {\rm cov}(\bar{x}_{1r}\bar{x}_{2(r+3)},\bar{x}_{1c}\bar{x}_{2(c+3)}) + {\rm cov}(\bar{x}_{2r}\bar{x}_{1(r+3)},\bar{x}_{2c}\bar{x}_{1(c+3)}) )\\
&\quad + ( {\rm cov}(\bar{x}_{1r}\bar{x}_{2(r+3)},\bar{x}_{2c}\bar{x}_{1(c+3)}) + {\rm cov}(\bar{x}_{2r}\bar{x}_{1(r+3)},\bar{x}_{1c}\bar{x}_{2(c+3)}) ).
\end{align*}
The off-diagonal entries of Σ can be derived similarly. This completes our proof.
With these moment and auto-covariance estimates, we are ready to construct our estimators for the parameters. In theory, we can obtain our parameter estimates by solving the system of moment equations using any general nonlinear root-finding algorithms. However, based on our extensive numerical experiments, we find that such an approach often leads to estimates with very large errors due to various reasons. Fortunately, we can overcome this problem by exploring the special characteristics of the equations of our interest and developing better numerical methods. In what follows, we first estimate the decay parameters k 1 and k 2, and then estimate the parameters in the marginal distribution of the process, that is, 
$\theta_1,\sigma_{x1},\theta_2$ and 
$\sigma_{x2}$. Details of our analysis are presented in the following two subsections.
3.1. Estimation of the decay parameters
In order to estimate the decay rates 
$e^{-k_1h}$ and 
$e^{-k_2h}$ of the two component processes, we make use of system of equations consisting of Eqs. (2.8) and (2.10)–(2.12). In principal, we can solve this system of equations to obtain 
$e^{-k_1h},e^{-k_2h},\theta_1\sigma_1$ and 
$\theta_2\sigma_2$. However, it is difficult to find the true roots by using general numerical algorithms, such as Newton–Raphson method. In what follows, we propose a numerical procedure to solve the system of equations which can achieve very good precision.
For notational simplicity, we rewrite the above system of equations as following:
\begin{eqnarray*}
v_1 + v_2 &=& b,\\
d_1v_1 + d_2v_2 &=& b_1,\\
d_1^2v_1 + d_2^2v_2 &=& b_2,\\
d_1^3v_1 + d_2^3v_2 &=& b_3,
\end{eqnarray*} where 
$v_1 \triangleq \theta_1\sigma_1, v_2 \triangleq \theta_2\sigma_2$, 
$b\triangleq{\rm var}(x_n)$, 
$b_j \triangleq {\rm cov}(x_n, x_{n+j}), j = 1,2,3$, 
$d_1 \triangleq e^{-k_1h}$ and 
$d_2 \triangleq e^{-k_2h}$. By using the first two equations, we have
\begin{equation*}
v_1 = \frac{-d_2b + b_1}{d_1 - d_2},\quad
v_2 = \frac{d_1b - b_1}{d_1 - d_2}.
\end{equation*}Further,
\begin{equation*}
d_2^2 = \frac{d_1b_2-b_3}{d_1b-b_1},\quad
d_2 = \frac{d_1^2b_1-b_3}{d_1^2b-b_2}.
\end{equation*}Thus,
\begin{equation*}
\frac{d_1b_2-b_3}{d_1b-b_1}
= \left(\frac{d_1^2b_1-b_3}{d_1^2b-b_2}\right)^2 ,
\end{equation*}which leads to the following quintic equation with unknown variable d 1
\begin{align}
&(bb_1^2-b^2b_2)\cdot d_1^{5} + (b^2b_3-b_1^3)\cdot d_1^4 + 2(bb_2^2-bb_1b_3)\cdot d_1^3 \nonumber\\
&+ 2(b_1^2b_3-bb_2b_3)\cdot d_1^2 + (bb_3^2-b_2^3)\cdot d_1 + (b_2^2b_3-b_1b_3^2)
= 0.
\end{align} The Jenkins–Traub algorithm for polynomial root-finding (see [Reference Jenkins and Traub19]) can be used to solve the quintic equation, an implementation of which is a function named polyroot in R programming language (see [25]). The roots returned by the algorithm are five complex numbers, among which we only need to keep those real-number roots that are between 0 and 1. Because of the symmetry between d 1 and d 2 (due to the symmetry of k 1 and k 2) d 2 must also be another root. Therefore, there should be at least two real-number roots that satisfy 
$d_2 = (d_1^2b_1-b_3)/(d_1^2b-b_2)$. We will use this property to find the correct roots for d 1 and d 2. In our extensive numerical experiments, we are able to find a pair of roots for d 1 and d 2 satisfying the required conditions.
We now are ready to derive the estimators for the decay parameters. Denote the sample version of Eq. (3.2) by
\begin{align}
&(\hat{b}\hat{b}_1^2-\hat{b}^2\hat{b}_2)\cdot \mathrm{x}^{5} + (\hat{b}^2\hat{b}_3-\hat{b}_1^3)\cdot \mathrm{x}^4 + 2(\hat{b}\hat{b}_2^2-\hat{b}\hat{b}_1\hat{b}_3)\cdot \mathrm{x}^3 \nonumber\\
&+ 2(\hat{b}_1^2\hat{b}_3-\hat{b}\hat{b}_2\hat{b}_3)\cdot \mathrm{x}^2 + (\hat{b}\hat{b}_3^2-\hat{b}_2^3)\cdot \mathrm{x} + (\hat{b}_2^2\hat{b}_3-\hat{b}_1\hat{b}_3^2)
= 0,
\end{align} where 
$\hat{b}$, 
$\hat{b}_1$, 
$\hat{b}_2$, 
$\hat{b}_3$ are S 2, 
$\hat{{\rm cov}}(x_n,x_{n+1})$, 
$\hat{{\rm cov}}(x_n,x_{n+2})$, 
$\hat{{\rm cov}}(x_n,x_{n+3})$, respectively. Let us denote the root obtained based on Eq. (3.3) for the estimate of d 1 by 
$\mathrm{x}^*$, that is, 
$\hat{d}_1 = \mathrm{x}^*$, then our estimators for d 2, v 1 (
$=\theta_1\sigma_1$), v 2 (
$=\theta_2\sigma_2$) are given by
\begin{align}
\hat{d}_2
&= \frac{\hat{d}_1^2\hat{b}_1 - \hat{b}_3 }{\hat{d}_1^2\hat{b} - \hat{b}_2},
\end{align}
\begin{align}
\hat{v}_1
&= \frac{-\hat{d}_2\hat{b} + \hat{b}_1 }{\hat{d}_1 - \hat{d}_2 },
\end{align}
\begin{align}
\hat{v}_2
&= \frac{\hat{d}_1\hat{b} - \hat{b}_1 }{\hat{d}_1 - \hat{d}_2 }.
\end{align} Before closing this subsection, we point out that there may exist further improvement as stated in what follows. In estimating of the decay rates, we have just used the first four auto-covariances 
${\rm cov}(x_n,x_n),\ldots, {\rm cov}(x_n,x_{n+3})$. Actually, 
$\forall j \geq 1$, we have
\begin{align*}
{\rm cov}(x_n,x_{n+j})
= e^{-jk_1h}\theta_1\sigma_1 + e^{-jk_2h}\theta_2\sigma_2.
\end{align*} One possible improvement is to make use of more these lagged auto-covariances. For instance, we can use 
${\rm cov}(x_n,x_{n+1}),{\rm cov}(x_n,x_{n+2}),{\rm cov}(x_n,x_{n+3}),{\rm cov}(x_n,x_{n+4})$ to construct another system of equations based on which we can produce another estimate of 
$(d_1,d_2)$. Then we average this estimate with the previous one, produced by the first four auto-covariances 
${\rm cov}(x_n,x_n),\ldots, {\rm cov}(x_n,x_{n+3})$, to obtain the final estimate, which should be more accurate. We can use more auto-covariances to improve the accuracy of our estimates.
3.2. Estimation of the marginal distribution parameters
In order to estimate the marginal distribution parameters, we make use of Eqs. (2.7) and (2.9). Since 
$\theta_1\sigma_1$ (
$=v_1$) and 
$\theta_2\sigma_2$ (
$=v_2$) can be estimated by Eqs. (3.5) and (3.6) respectively, we rewrite 
${\rm cm}_3[x_n]$ as 
${\rm cm}_3[x_n] = 2v_1^2/\theta_1 + 2v_2^2/\theta_2$. Then we have the following quadratic equation
\begin{equation}
a_1\theta_1^2 + a_2\theta_1 + a_3 = 0,
\end{equation}with coefficiencies
\begin{align*}
a_1 \triangleq {\rm cm}_3[x_n],\quad
a_2 \triangleq 2v_2^2 - 2v_1^2 - {\rm cm}_3[x_n]E[x_n],\quad
a_3 \triangleq 2v_1^2E[x_n].
\end{align*}Eq. (3.7) has two solutions
\begin{equation*}
\mathrm{x}_1 = \frac{-a_2 + \sqrt{\Delta}}{2a_1},\quad
\mathrm{x}_2 = \frac{-a_2 - \sqrt{\Delta}}{2a_1},
\end{equation*} where 
$\Delta = a_2^2 - 4a_1a_3 = 4(\theta_1\theta_2)^2(\sigma_1^2 - \sigma_2^2)^2$. We can show that only one equals θ 1. If 
$\sigma_1 \gt \sigma_2$, we have
\begin{align*}
\mathrm{x}_1
= \frac{(\theta_1\sigma_1)^2 + \theta_1\theta_2\sigma_1^2}{\theta_1\sigma_1^2 + \theta_2\sigma^2},\quad
\mathrm{x}_2 = \theta_1.
\end{align*}Otherwise, we have
\begin{align*}
\mathrm{x}_1 = \theta_1,\quad
\mathrm{x}_2 = \frac{(\theta_1\sigma_1)^2 + \theta_1\theta_2\sigma_1^2}{\theta_1\sigma_1^2 + \theta_2\sigma^2}.
\end{align*} In determining whether 
$\sigma_1 \gt \sigma_2$, we only need to verify if 
$v_1/\mathrm{x}_2 \lt v_2/\theta_2$. Assuming 
$\sigma_1 \gt \sigma_2$, then 
$\mathrm{x}_2=\theta_1$ and
\begin{align*}
\theta_2 = E[x_n] - \mathrm{x}_2,\quad
\sigma_1 = v_1/\mathrm{x}_2,\quad
\sigma_2 = v_2/\theta_2.
\end{align*}Denote the sample version of Eq. (3.7) as
\begin{equation}
\hat{a}_1\mathrm{x}^2 + \hat{a}_2\mathrm{x} + \hat{a}_3 = 0,
\end{equation} with 
$\hat{a}_1$, 
$\hat{a}_2$, 
$\hat{a}_3$ being the sample estimates of a 1, a 2, a 3, respectively. Let us denote the root obtained based on Eq. (3.8) for θ 1 by 
$\mathrm{x}^*$, that is, 
$\hat{\theta}_1 = \mathrm{x}^*$, then the other estimators are given by
\begin{equation*}
\hat{\theta}_2 = \overline{X} - \hat{\theta}_1,\quad
\hat{\sigma}_1 = \hat{v}_1/\hat{\theta}_1,\quad
\hat{\sigma}_2 = \hat{v}_2/\hat{\theta}_2.
\end{equation*}Finally, we have
\begin{equation*}
\hat{k}_1 = -\log \hat{d}_1/h,\quad
\hat{k}_2 = -\log \hat{d}_2/h,\quad
\hat{\sigma}_{x1} = \sqrt{2\hat{\sigma}_1\hat{k}_1},\quad
\hat{\sigma}_{x2} = \sqrt{2\hat{\sigma}_2\hat{k}_2}.
\end{equation*} We can define moment Eqs. (2.7)–(2.12) as a mapping 
$f: \mathbb{R}^6\rightarrow\mathbb{R}^6$, that is,
\begin{equation*}
f(\theta_1,\theta_2,\sigma_1,\sigma_2,d_1,d_2) = \boldsymbol{\gamma},
\end{equation*}where γ, by definition, represents the vector of the first moment, the second central moment and the third central moment and the first three auto-covariances of the process xn.
Let Jf be the Jacobian of f, which is a 
$6\times 6$ matrix of partial derivatives of f with respect to the entries of f. Taking the first row of Jf as an example, it is the gradient of 
$E[x_n]$ with respect to 
$(\theta_1,\theta_2,\sigma_1,\sigma_2,d_1,d_2)^T$, that is,
\begin{equation*}
\left(\frac{\partial E[x_n]}{\partial \theta_1}, \ldots, \frac{\partial E[x_n]}{\partial d_2}\right).
\end{equation*}With some calculations, we have
\begin{equation*}
J_f = \left[
\begin{matrix}
1 &1 &0 &0 &0 &0\\
\sigma_1 &\sigma_2 &\theta_1 &\theta_2 &0 &0\\
2\sigma_1^2 &2\sigma_2^2 &4\theta_1\sigma_1 &4\theta_2\sigma_2 &0 &0\\
d_1\sigma_1 &d_2\sigma_2 &d_1\theta_1 &d_2\sigma_2 &\theta_1\sigma_1 &\theta_2\sigma_2\\
d_1^2\sigma_1 &d_2^2\sigma_2 &d_1^2\theta_1 &d_2^2\sigma_2 &2d_1\theta_1\sigma_1 &2d_2\theta_2\sigma_2\\
d_1^3\sigma_1 &d_2^3\sigma_2 &d_1^3\theta_1 &d_2^3\sigma_2 &3d_1^2\theta_1\sigma_1 &3d_2^2\theta_2\sigma_2
\end{matrix} \right].
\end{equation*} Though the inverse function 
$f^{-1}(\boldsymbol{\gamma})$ does not have an explicit expression, we will show that the Jacobian Jf is invertible, thus 
$f^{-1}(\boldsymbol{\gamma})$ exists by the inverse function theorem.
We further define our final parameter estimators as another mapping 
$g:\mathbb{R}^6\rightarrow\mathbb{R}^6$, that is,
\begin{equation*} g(\hat{\theta}_1,\hat{\theta}_2,\hat{\sigma}_1,\hat{\sigma}_2,\hat{d}_1,\hat{d}_2) = (\hat{\theta}_1,\hat{\theta}_2,\hat{\sigma}_{x1},\hat{\sigma}_{x2},\hat{k}_1,\hat{k}_2)^T,
\end{equation*}whose Jacobian, denoted by Jg, is given as the following
\begin{equation*}
J_g = \left[
\begin{matrix}
1 &0 &0 &0 &0 &0\\
0 &1 &0 &0 &0 &0\\
0 &0 &\frac{-\log d_1/h}{\sqrt{-2\sigma_1\log d_1/h}} &0 &\frac{-\sigma_1/(d_1h)}{\sqrt{-2\sigma_1\log d_1/h}} &0\\
0 &0 &0 &\frac{-\log d_2/h}{\sqrt{-2\sigma_2\log d_2/h}} &0 &\frac{-\sigma_2/(d_2h)}{\sqrt{-2\sigma_2\log d_2/h}}\\
0 &0 &0 &0 &-\frac{1}{d_1h} &0\\
0 &0 &0 &0 &0 &-\frac{1}{d_2h}
\end{matrix}
\right].
\end{equation*} We first present the following central limit theorem for the parameter estimators 
$(\hat{\theta}_1,\hat{\theta}_2,\hat{\sigma}_{1},\hat{\sigma}_{2},\hat{d}_1,\hat{d}_2)^T$.
Theorem 3.2 Suppose the superposition of two square-root diffusions described by Eqs. (2.1)–(2.3) does not degenerate into a one square-root diffusion, that is, 
$d_1\neq d_2$, 
$\theta_1\neq \theta_2$, and 
$\sigma_1\neq \sigma_2$. Then the parameter estimators 
$(\hat{\theta}_1,\hat{\theta}_2,\hat{\sigma}_{1},\hat{\sigma}_{2},\hat{d}_1,\hat{d}_2)^T$ exist with probability tending to one and satisfy
\begin{equation}
\lim_{N\rightarrow\infty} \sqrt{N}( (\hat{\theta}_1,\hat{\theta}_2,\hat{\sigma}_{1},\hat{\sigma}_{2},\hat{d}_1,\hat{d}_2)^T - (\theta_1,\theta_2,\sigma_{1},\sigma_{2},d_1,d_2)^T) \overset{d}{=}\mathcal{N}(\boldsymbol{0}, J_f^{-1}\Sigma (J_f^{-1})^T).
\end{equation}Proof. We first prove the Jacobian Jf is invertible. With some elementary row operations, Jf is equivalent to the following matrix
\begin{equation*}
J_1 \triangleq \left[
\begin{matrix}
1 &1 &0 &0 &0 &0\\
0 &1 &\frac{\theta_1}{\sigma_2-\sigma_1} &\frac{\theta_2}{\sigma_2-\sigma_1} &0 &0\\
0 &0 &1 &-\frac{\theta_2}{\theta_1} &0 &0\\
0 &0 &0 &a_{44} &\theta_1\sigma_1 &\theta_2\sigma_2\\
0 &0 &0 &a_{54} &2d_1\theta_1\sigma_1 &2d_2\theta_2\sigma_2\\
0 &0 &0 &a_{64} &3d_1^2\theta_1\sigma_1 &3d_2^2\theta_2\sigma_2
\end{matrix}
\right],
\end{equation*}where
\begin{align*}
a_{44} &\triangleq (d_1+d_2)\theta_2 - \frac{2\theta_2}{\sigma_2-\sigma_1}(d_2\sigma_2-d_1\sigma_1),\\
a_{54} &\triangleq (d_1^2+d_2^2)\theta_2 - \frac{2\theta_2}{\sigma_2-\sigma_1}(d_2^2\sigma_2-d_1^2\sigma_1),\\
a_{64} &\triangleq (d_1^3+d_2^3)\theta_2 - \frac{2\theta_2}{\sigma_2-\sigma_1}(d_2^3\sigma_2-d_1^3\sigma_1).
\end{align*}Therefore, the invertibility of Jf depends on that of the bottom right submatrix in J 1, that is,
\begin{equation*}
J_2 \triangleq \left[
\begin{matrix}
a_{44} &\theta_1\sigma_1 &\theta_2\sigma_2\\
a_{54} &2d_1\theta_1\sigma_1 &2d_2\theta_2\sigma_2\\
a_{64} &3d_1^2\theta_1\sigma_1 &3d_2^2\theta_2\sigma_2
\end{matrix}
\right].
\end{equation*}With elementary row operations, J 2 is equivalent to the following matrix
\begin{equation*}
J_3 \triangleq \left[
\begin{matrix}
a_{11} &3(d_2^2-d_1^2)\theta_1\sigma_1 &0\\
a_{21}(d_1+d_2)/d_1-a_{11} &0 &0\\
a_{64} &3d_1^2\theta_1\sigma_1 &3d_2^2\theta_2\sigma_2
\end{matrix}
\right],
\end{equation*}where
\begin{align*}
a_{11} &\triangleq (3d_1d_2^2 + 2d_2^3 - d_1^3)\theta_2 - \frac{2\theta_2}{\sigma_2-\sigma_1}(2d_2^3\sigma_2-3d_1d_2^2\sigma_1+d_1^3\sigma_1),\\
a_{21} &\triangleq \left(\frac{3}{2}d_1^2d_2 + \frac{1}{2}d_2^3 - d_1^3\right)\theta_2 - \frac{2\theta_2}{\sigma_2-\sigma_1}\left(\frac{1}{2}d_2^3\sigma_2 - \frac{3}{2}d_1^2d_2\sigma_1 + d_1^3\sigma_1\right).
\end{align*} Thus, the invertibility of Jf reduces to whether the term 
$a_{21}(d_1+d_2)/d_1 - a_{11}$ equals zero or not. After some calculations, we have
\begin{align*}
a_{21}(d_1+d_2)/d_1 - a_{11}
&= \theta_2\frac{\sigma_1+\sigma_2}{\sigma_2-\sigma_1}\frac{d_2^4}{2d_1}\left[\left(\frac{d_1}{d_2}\right)^3 - 3\left(\frac{d_1}{d_2}\right)^2 + 3\left(\frac{d_1}{d_2}\right) -1 \right]\\
&= \theta_2\frac{\sigma_1+\sigma_2}{\sigma_2-\sigma_1}\frac{d_2^4}{2d_1}\left(\frac{d_1}{d_2}-1\right)^3.
\end{align*} Note that 
$d_1\neq d_2$. Therefore, 
$a_{21}(d_1+d_2)/d_1-a_{11}$ does not equal zero, consequently the Jacobian Jf is invertible.
With the covariance matrix Σ in Theorem 3.1, it is apparently
\begin{equation}
E[x_n^2 + \bar{x}_n^4 + \bar{x}_n^6 + \bar{x}_n^2\bar{x}_{n+1}^2 + \bar{x}_n^2\bar{x}_{n+2}^2 + \bar{x}_n^2\bar{x}_{n+3}^2] \lt \infty,
\end{equation} where 
$\bar{x}_{n+j} \triangleq x_{n+j} - E[x_n], j=0,1,2,3$.
In summary, we have verified: (1) the mapping f from parameters 
$(\theta_1,\theta_2,\sigma_{1},\sigma_{2},d_1,d_2)^T$ to moments γ, are continuously differentiable with nonsingular Jacobian Jf, and (2) the summation of the double order moments is finite, that is, Eq. (3.10). Therefore, by applying Theorem 4.1 in [Reference Van der Vaart26], we have Theorem 3.2. This completes the proof.
We now present the central limit theorem for our parameter estimators 
$(\hat{\theta}_1,\hat{\theta}_2,\hat{\sigma}_{x1},\hat{\sigma}_{x2},\hat{k}_1,\hat{k}_2)^T$.
Theorem 3.3 Suppose the same assumption as in Theorem 3.2 holds. Then,
\begin{equation}
\lim_{N\rightarrow\infty} \sqrt{N}( (\hat{\theta}_1,\hat{\theta}_2,\hat{\sigma}_{x1},\hat{\sigma}_{x2},\hat{k}_1,\hat{k}_2)^T - (\theta_1,\theta_2,\sigma_{x1},\sigma_{x2}, k_1, k_2)^T) \overset{d}{=}\mathcal{N}(\boldsymbol{0}, J_gJ_f^{-1}\Sigma (J_f^{-1})^TJ_g^T).
\end{equation}Proof. Note that the mapping 
$g(\theta_1,\theta_2,\sigma_1,\sigma_2,d_1,d_2)$ takes the following expression
\begin{equation*}
\begin{bmatrix}
\theta_1\\
\theta_2\\
\sigma_{x1}\\
\sigma_{x2}\\
k_1\\
k_2
\end{bmatrix}
=
\begin{bmatrix}
\theta_1\\
\theta_2\\
\sqrt{-2\sigma_1\log d_1/h}\\
\sqrt{-2\sigma_2\log d_2/h}\\
-\log d_1 /h\\
-\log d_2 / h
\end{bmatrix}
\equiv g(\theta_1,\theta_2,\sigma_1,\sigma_2,d_1,d_2),
\end{equation*} which is differentiable and has the Jacobian Jg. Meanwhile, we have verified the convergence of the estimators 
$(\hat{\theta}_1,\hat{\theta}_2,\hat{\sigma}_{1},\hat{\sigma}_{2},\hat{d}_1,\hat{d}_2)^T$ in Theorem 3.2. Therefore, by applying the delta method (Theorem 3.1 in [Reference Van der Vaart26]), we have the convergence in Eq. (3.11). This completes the proof.
4. Numerical experiments
In this section, we conduct numerical experiments to test the estimators derived in the previous section. First, we validate the accuracy of our estimators under different parameter value settings. Then, we analyze the asymptotic performances of our estimators as the sample length increases.
In the first set of experiments, we consider four different combinations of parameter values, with S0 as the base combination in which 
$k_1=2$, 
$\theta_1=1.5$, 
$\sigma_{x1}=1.6$, 
$k_2=0.2$, 
$\theta_2=0.5$, 
$\sigma_{x2}=0.2$. Each of the other three combinations differs from S0 in only one pair of parameter values: S1 increases 
$(k_1,k_2)$’s values to (3,0.2), S2 increases 
$(\theta_1,\theta_2)$’s values to (3,1), S3 decreases 
$(\sigma_{x1},\sigma_{x2})$’s values to (0.8,0.1).
The transition distribution of 
$x_{i}(t)$ given 
$x_{i}(s)$ (
$i=1,2$) for s < t is a noncentral chi-squared distribution multiplied with a scale factor (see [Reference Broadie and Kaya7, Reference Cox, Ingersoll and Ross12]), that is,
\begin{equation*}
x_i(t) = \frac{\sigma_{xi}^2[1-e^{-k_i(t-s)}]}{4k_i}\chi'^2_d\left(\frac{4k_ie^{-k_i(t-s)}}{\sigma_{xi}^2[1-e^{-k_i(t-s)}]}x_{i}(s) \right), \quad s \lt t,
\end{equation*} where 
$\chi'^2_d(\lambda)$ represents the noncentral chi-squared random variable with d degrees of freedom and noncentrality parameter λ, and 
$d=4k_i\theta_i/\sigma_{xi}^2$. Therefore, we use this transition function to generate sample observations of x(t) and set the time interval, between any two points, h = 1. For each parameter setting, we run 400 replications with 1000K samples for each replication. The numerical results are presented in Table 1 with the format “mean ± standard deviation” based on these 400 replications (the format remains the same for all numerical results). The results illustrate our estimators are fairly accurate.
Table 1. Numerical results under different parameter settings.
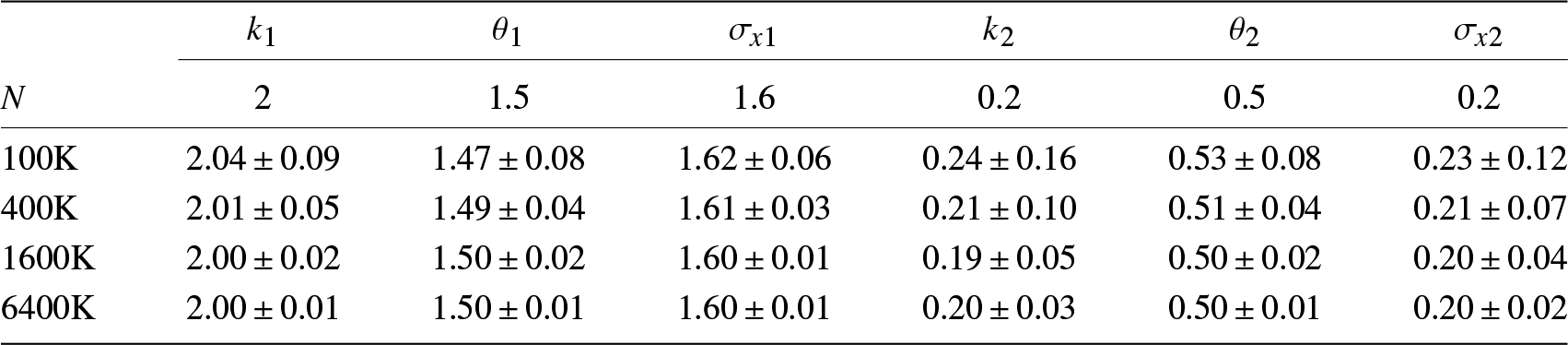
To test the effect of N on the performance of our estimators, we run the second set of experiments in which we increase N from 100K to 6400K for S0, while all other settings remain the same. The results are given in Table 2, which demonstrates as N increases the accuracy of our estimators improve approximately at the rate of 
$1/\sqrt{N}$.
Table 2. Asymptotic behavior as N increases.
5. Conclusion
In this paper, we consider the problem of parameter estimation for the superposition of two square-root diffusions. We first derive their moments and auto-covariances based on which we develop our MM estimators. A major contribution of our method is that we only employ low order moments and auto-covariances and find an efficient way to solve the system of moment equations which produces very good estimates. Our MM estimators are accurate and easy to implement. We also establish the central limit theorem for our estimators in which the explicit formulas for the asymptotic covariance matrix are given. Finally, we conduct numerical experiments to test and validate our method. The MM proposed in this paper can be potentially applied to other extensions, such as including jumps in the component process or the superposed process. This is a possible future research direction.
Acknowledgments
This work is supported in part by the National Nature Science Foundation of China (NSFC) under grants 72033003 and 72350710219.
Conflict of interest
The authors declare that they have no conflict of interest.
Appendix
Asymptotic covariance matrix entries calculation
With slight abuse of notation, we use xn to denote either 
$x_{1n}$ or 
$x_{2n}$ and 
$\bar{x}_n$ for either 
$\bar{x}_{1n}$ or 
$\bar{x}_{1n}$ to simplify the notations, and similarly, use 
$k,\theta,\sigma$ for either 
$k_1,\theta_1,\sigma_{x1}$ or 
$k_2,\theta_2,\sigma_{x2}$. In order to calculate the asymptotic variances and covariances, we need the following approximate equations (we also call them as the decay equations), 
$\forall n \ge 0$:
\begin{align}
\bar{x}_{n}
&\approx e^{-nkh}\bar{x}_{0},
\end{align}
\begin{align}
\bar{x}_{n}^2
&\approx e^{-2nkh}\bar{x}_{0}^2 + (e^{-nkh}- e^{-2nkh})\bar{x}_{0}\frac{\sigma^2}{k} + c_2,
\end{align}
\begin{align}
\bar{x}_{n}^3
&\approx e^{-3nkh}\bar{x}_{0}^3 + (e^{-2nkh} - e^{-3nkh})\bar{x}_{0}^2 \frac{3\sigma^2}{k}
+ (e^{-nkh}-e^{-3nkh})\bar{x}_{0}\frac{3\sigma^2\theta}{2k}\nonumber\\
&\quad + (e^{-nkh} - 2e^{-2nkh} + e^{-3nkh})\bar{x}_{0}\frac{3\sigma^4}{2k^2} + c_3,
\end{align}by eliminating the martingale parts, where
\begin{align*}
&c_2 \triangleq (1-e^{-2nkh})\frac{\sigma^2\theta}{2k},\quad
c_3 \triangleq (1-3e^{-2nkh}+2e^{-3nkh})\frac{\sigma^4\theta}{2k^2}.
\end{align*}The derivation of above equations is given later.
Let us use
\begin{equation*}
dx(t) = k(\theta-x(t))dt + \sigma\sqrt{x(t)}dw(t)
\end{equation*}to denote the component process either Eq. (2.2) or (2.3), for notation simplification. Then, by introducing the following notation
\begin{equation*}
IE_{t} \triangleq \int_{0}^{t}e^{ks}\sqrt{x(s)}dw(s),\quad IE_{n} \triangleq IE_{nh},
\end{equation*}we have
\begin{align*}
x(t)
&= e^{-kt}x(0) + \theta\left[1-e^{-kt}\right] + \sigma e^{-kt}IE_{t}, \quad\forall t \geq 0,\\
\bar{x}_n
&= e^{-knh}\bar{x}_0 + \sigma e^{-knh} IE_n, \quad\quad\quad\forall n = 0,1,2,\ldots.
\end{align*}Therefore,
\begin{equation*}
\bar{x}_n^m = \sum_{j=0}^m C_m^j \left(e^{-knh}\bar{x}_0\right)^j\left(\sigma e^{-knh}IE_{n}\right)^{m-j}, m=1,2,3,4.
\end{equation*} Taking 
$\bar{x}_n^2$ as an example, we show how to obtain its approximation. By Itô calculus,
\begin{align*}
dIE_t^2
&= 2IE_{t}e^{kt}\sqrt{x(t)}dw(t) + e^{2kt}x(t)dt,\\
IE_t^2
&= 2\int_0^t IE_{s}e^{ks}\sqrt{x(s)}dw(s) + \int_0^t e^{2ks}x(s)ds.
\end{align*}Note that
\begin{equation*}
E\left[ \int_0^t IE_{s}e^{ks}\sqrt{x(s)}dw(s) \right] = 0,
\end{equation*}thus, by deleting this term, we have following approximation
\begin{equation*}
IE_t^2 \approx \int_0^t e^{2ks}x(s)ds.
\end{equation*}Furthermore,
\begin{align*}
\int_0^t e^{2ks}x(s)ds
&= \frac{e^{kt}-1}{k}\bar{x}_0 + \frac{e^{2kt}-1}{2k}\theta + \int_0^t \sigma e^{ks}IE_s ds\\
&\approx \frac{e^{kt}-1}{k}\bar{x}_0 + \frac{e^{2kt}-1}{2k}\theta,
\end{align*}by deleting the third term in the right hand of the first equation because its expectation is also zero, that is,
\begin{equation*}
E\left[ \int_0^t \sigma e^{ks}IE_s ds \right] = 0.
\end{equation*}Letting t = nh, we have
\begin{equation*}
IE_n^2 \approx \frac{e^{knh}-1}{k}\bar{x}_0 + \frac{e^{2knh}-1}{2k}\theta.
\end{equation*}Therefore,
\begin{align*}
\bar{x}_n^2
&\approx e^{-2nkh}\bar{x}_0^2 + \left(e^{-nkh}- e^{-2nkh}\right)\bar{x}_0\frac{\sigma^2}{k} + \left(1 - e^{-2nkh}\right)\frac{\sigma^2\theta}{2k}
\end{align*}by deleting all those terms having expectation 0. The results for all other cases can be derived similarly.
With these approximation formulas, we can easily compute the following auto-covariances
\begin{equation*}
{\rm cov}(x_r,z_c^m), {\rm cov}(z_r^{m_1},z_c^{m_2}), m,m_1,m_2=1,2,3,4,
\end{equation*} for example, 
$\forall c \geq r$,
\begin{equation*}
{\rm cov}(x_r,z_c^1)
= e^{-2(c-r)kh}{\rm cov}(x_r,\bar{x}_r^2) + (e^{-(c-r)kh}-e^{-2(c-r)kh})\frac{\sigma^2}{k}{\rm cov}(x_r,\bar{x}_r),
\end{equation*}noting that 
$z_c^1 = \bar{x}_c^2$ by definition.
By omitting the tedious intermediate steps, we present the results in following two subsections.
On-diagonal entries
\begin{align*}
c_{11,1}
&\triangleq (1+2e_{11}){\rm var}(x_{1n}) =(1+2e_{11})\frac{\theta_1\sigma_{x1}^2}{2k_1},\\[-1pt]
c_{22,1}
&\triangleq (1+2e_{12}){\rm var}(\bar{x}_{1n}^2) + 2(e_{11}-e_{12})\frac{\sigma_{x1}^2}{k_1}{\rm cm}_3[x_{1n}]\\[-1pt]
&\quad + 2(1+2e_{1,1}){\rm var}(x_{1n}){\rm var}(x_{2n}),\\[-1pt]
c_{33,1}
&\triangleq (1+2e_{13}){\rm var}(\bar{x}_{1n}^3) + 2(e_{12}-e_{13})\frac{3\sigma_{x1}^2}{k_1}{\rm cov}(\bar{x}_{1n}^3,\bar{x}_{1n}^2)\\[-1pt]
&\quad + 2\left[ (e_{11}-e_{13})\frac{3\sigma_{x1}^2\theta_1}{2k_1} + (e_{11}-2e{12}+e_{13})\frac{3\sigma_{x1}^4}{2k_1^2}\right]{\rm cm}_4[x_{1n}]\\[-1pt]
&\quad + 3(5+2e_{11}+6e_{2,1}){\rm cm}_4[x_{1n}]{\rm var}(x_{2n})
+ 18(1+e_{1,2}){\rm cm}_3[x_{1n}]{\rm cm}_3[x_{2n}]\\[-1pt]
&\quad + 18\left[(e_{1,1}-e_{2,1})\frac{\sigma_{x1}^2}{k_1} + (e_{1,1}-e_{1,2})\right]{\rm cm}_3[x_{1n}]{\rm var}(x_{2n})\\[-1pt]
&\quad + 18(e_{21}-e_{2,1}){\rm var}^2(x_{1n}){\rm var}(x_{2n}) \\[-1pt]
&\quad + 6e_{23}{\rm var}(x_{1n}){\rm cm}_4[x_{2n}] + 6(e_{22}-e_{23})\frac{3\sigma_{x2}^2}{k_2}{\rm var}(x_{n1}){\rm cm}_3[x_{2n}]\\[-1pt]
&\quad + 6\left[ (e_{21}-e_{23})\frac{3\sigma_{x2}^2\theta_2}{2k_2} + (e_{21}-2e_{22}+e_{23})\frac{3\sigma_{x2}^4}{2k_2^2} \right]{\rm var}(x_{1n}){\rm var}(x_{2n}),\\[-1pt]
c_{44,1}
&\triangleq {\rm var}(\bar{x}_{1n}\bar{x}_{1(n+1)}) + 2e_{12}e^{k_1h}{\rm cov}(\bar{x}_{1n}\bar{x}_{1(n+1)},\bar{x}_{1(n+1)}^2)\\[-1pt]
&\quad + 2(e_{11}-e_{12}e^{k_1h})\frac{\sigma_{x1}^2}{k_1}{\rm cov}(\bar{x}_{1n}\bar{x}_{1(n+1)},\bar{x}_{1(n+1)})\\[-1pt]
&\quad + \left[1 + 2e_{1,1} + e^{-(k_1+k_2)h} \right]{\rm var}(x_{1n}){\rm var}(x_{2n})\\[-1pt]
&\quad + \left[ \left(e^{-2k_1h} + e^{-2k_1h}e_{1,1}\right) + \left( e^{-2k_2h} + e^{-2k_2h}e_{1,1} \right) \right]{\rm var}(x_{1n}){\rm var}(x_{2n}),\\[-1pt]
c_{55,1} &\triangleq {\rm var}(\bar{x}_{1n}\bar{x}_{1(n+2)}) + 2{\rm cov}(\bar{x}_{1n}\bar{x}_{1(n+2)},\bar{x}_{1(n+1)}\bar{x}_{1(n+3)})\\
&\quad + 2e_{12}{\rm cov}(\bar{x}_{1n}\bar{x}_{1(n+2)},\bar{x}_{1(n+2)}^2)\\[-1pt]
&\quad + 2(e_{11}e^{-k_1h}-e_{12})\frac{\sigma_{x1}^2}{k_1}{\rm cov}(\bar{x}_{1n}\bar{x}_{1(n+2)},\bar{x}_{1(n+2)})\\[-1pt]
&\quad + \left[ 1 + 2e_{1,1} + e^{-2(k_1+k_2)h} \right]{\rm var}(x_{1n}){\rm var}(x_{2n})\\[-1pt]
&\quad + \left[ e^{-(3k_1+k_2)h} + e^{-4k_1h} + e^{-4k_1h} e_{1,1} \right]{\rm var}(x_{1n}){\rm var}(x_{2n})\\[-1pt]
&\quad + \left[ e^{-(k_1+3k_2)h} + e^{-4k_2h} + e^{-4k_2h}e_{1,1} \right]{\rm var}(x_{1n}){\rm var}(x_{2n}),\\
c_{66,1}
&\triangleq {\rm var}(\bar{x}_{1n}\bar{x}_{1(n+3)}) + 2{\rm cov}(\bar{x}_{1n}\bar{x}_{1(n+3)},\bar{x}_{1(n+1)}\bar{x}_{1(n+4)})\\
&\quad + 2{\rm cov}(\bar{x}_{1n}\bar{x}_{1(n+3)},\bar{x}_{1(n+2)}\bar{x}_{1(n+5)}) + 2e_{12}e^{-k_1h}{\rm cov}(\bar{x}_{1n}\bar{x}_{1(n+3)},\bar{x}_{1(n+3)}^2)\\
&\quad + 2(e_{11}e^{-2k_1h}-e_{12}e^{-k_1h})\frac{\sigma_{x1}^2}{k_1}{\rm cov}(\bar{x}_{1n}\bar{x}_{1(n+3)},\bar{x}_{1(n+3)})
\end{align*}
\begin{align*}
&\quad + \left[1+2e_{1,1} + e^{-3(k_1+k_2)h} \right]{\rm var}(x_{1n}){\rm var}(x_{2n})\\
&\quad + \left[ e^{-(4k_1+2k_2)h} + e^{-(5k_1+k_2)h} + e^{-6k_1h} + e^{-6k_1h}e_{1,1} \right]{\rm var}(x_{1n}){\rm var}(x_{2n})\\
&\quad + \left[ e^{-(2k_1+4k_2)h} + e^{-(k_1+5k_2)h} + e^{-6k_2h} + e^{-6k_2h}e_{1,1} \right]{\rm var}(x_{1n}){\rm var}(x_{2n}).
\end{align*} The terms 
${\rm cm}_3[x_{1n}], {\rm cm}_4[x_{1n}], {\rm var}(\bar{x}_{1n}^3)$ and so on are easy to compute with Eq. (2.5). It is also straightforward to compute terms like 
${\rm cov}(\bar{x}_{1n}\bar{x}_{1(n+3)},\bar{x}_{1(n+1)}\bar{x}_{1(n+4)})$ by employing Eqs. (A.1)–(A.3). We omit their explicit formulas here.
Terms 
$c_{nn,2}$ (
$n=1,\ldots,6$) are defined similarly by replacing 
$e_{1j}$ (
$j=1,\ldots,4$) in 
$c_{nn,1}$ with 
$e_{2j}$, 
$x_{1n}$ with 
$x_{2n}$, and 
$k_1,\theta_1,\sigma_{x1}$ with 
$k_2,\theta_2,\sigma_{x2}$, respectively, and vice versa.
Off-diagonal entries
Definitions of 
$c_{12,1},c_{13,1},c_{14,1},c_{15,1},c_{16,1}$ are given as following:
\begin{align*}
c_{12,1}
&\triangleq (1+e_{11}+e_{12}){\rm cm}_3[{x_{1n}}] + (e_{11}-e_{12})\frac{\sigma_{x1}^2}{k_1}{\rm var}(x_{1n}),\\[1.5pt]
c_{13,1}
&\triangleq (1+e_{11}+e_{13}){\rm cm}_4[x_{1n}]
+ (e_{12}-e_{13})\frac{3\sigma_{x1}^2}{k_1}{\rm cm}_3[x_{1n}]\\[1.5pt]
&\quad + \left[ (e_{11}-e_{13})\frac{3\sigma_{x1}^2\theta_1}{2k_1} + (e_{11}-2e_{12}+e_{13})\frac{3\sigma_{x1}^4}{2k_1^2}\right]{\rm var}(x_{1n}) \\[1.5pt]
&\quad + 3(1+2e_{11}){\rm var}(x_{1n}){\rm var}(x_{2n}),\\[1.5pt]
c_{14,1}
&\triangleq (1+e_{11}+e_{12})e^{-k_1h}{\rm cm}_3[x_{1n}] + (e_{11}-e_{12})e^{-k_1h}{\rm var}(x_{1n})\\[1.5pt]
&\quad +e_{11}(1-e^{-k_1h})\frac{\sigma_{x1}^2}{k_1}{\rm var}(x_{1n}),\\[1.5pt]
c_{15,1}
&\triangleq \left[1+e_{12} + (1+e_{11})e^{-k_1h}\right]e^{-2k_1h}{\rm cm}_3[x_{1n}] + (e_{11}-e_{12})e^{-2k_1h}{\rm var}(x_{1n})\\[1.5pt]
&\quad + \left[e_{11}(e^{-k_1h}-e^{-3k_1h}) + e^{-2k_1h}-e^{-3k_1h})\frac{\sigma_{x1}^2}{k_1}\right]{\rm var}(x_{1n}),
\end{align*}
\begin{align*}
\\[-40pt]
c_{16,1}
&\triangleq (1+e_{12})e^{-3k_1h}{\rm cov}(\bar{x}_{1n},\bar{x}_{1n}^2) + (e_{11}-e_{12})e^{-3k_1h}\frac{\sigma_{x1}^2}{k_1}{\rm var}(\bar{x}_{1n})\\[1.5pt]
&\quad + {\rm cov}(\bar{x}_{1(n+1)},\bar{x}_{1n}\bar{x}_{1(n+3)}) + {\rm cov}(\bar{x}_{1(n+2)},\bar{x}_{1n}\bar{x}_{1(n+3)}) \\[1.5pt]
&\quad + (1+e_{11}){\rm cov}(\bar{x}_{1(n+3)},\bar{x}_{1n}\bar{x}_{1(n+3)}).
\end{align*} Again, terms 
$c_{1n,2}$ (
$n=2,\ldots,6$) are defined similarly by substituting 
$e_{1j}$ (
$j=1,\ldots,4$) in 
$c_{1n,1}$ with 
$e_{2j}$, 
$x_{1n}$ with 
$x_{2n}$, 
$x_{2n}$ with 
$x_{1n}$, and 
$k_1,\theta_1,\sigma_{v1}$ with 
$k_2,\theta_2,\sigma_{v2}$, respectively, and vice versa. The other terms 
$c_{lm,2}$ (
$l\neq 1, l\neq m$) are defined similarly according to 
$c_{lm,1}$ in the following formulas.
\begin{align*}
c_{23,1}
&\triangleq (1+e_{12}+e_{13}){\rm cov}(\bar{x}_{1n}^2,\bar{x}_{1n}^3)
+ (e_{11}-e_{12})\frac{\sigma_{x1}^2}{k_1}{\rm cm}_4[x_{1n}]\\[1.5pt]
&\quad + (e_{12}-e_{13})\frac{3\sigma_{x1}^2}{k_1}{\rm cov}(\bar{x}_{1n}^2,\bar{x}_{1n}^2)\\[1.5pt]
&\quad + \left[ (e_{11}-e_{13})\frac{3\sigma_{x1}^2\theta_1}{2k_1} + (e_{11}-2e_{12}+e_{13})\frac{3\sigma_{x1}^4}{2k_1^2}\right] {\rm cm}_3[x_{1n}]\\[1.5pt]
&\quad + (9+3e_{11}+3e_{12}+6e_{1,1}+6e_{2,1}){\rm cm}_3[x_{1n}]{\rm var}(x_{2n})\\[1.5pt]
&\quad + (3e_{11}-3e_{12}+6e_{1,1}-6e_{2,1})\frac{\sigma_{x1}^2}{k_1}{\rm var}(x_{1n}){\rm var}(x_{2n}),
\end{align*}
\begin{align*}
\\[-48pt]
c_{24,1}
&\triangleq (1+e_{12})e^{-k_1h}{\rm var}(\bar{x}_{1n}^2) + (e_{11}-e_{12})\frac{\sigma_{x1}^2}{k_1}e^{-k_1h}{\rm cm}_3[x_{1n}]\\[1.5pt]
&\quad + e_{11}e^{k_1h}{\rm cov}(\bar{x}_{1(n+1)}^2,\bar{x}_{1n}\bar{x}_{1(n+1)})\\[1.5pt]
&\quad + (e_{11}e^{k_1h}-e_{12}e^{2k_1h})\frac{\sigma_{x1}^2}{k_1}E[\bar{x}_{1n}\bar{x}_{1(n+1)}^2]\\[1.5pt]
&\quad + 2(e_{1,1}e^{-k_2h} + e^{-k_2h} + e_{1,1}e^{k_2h}){\rm var}(x_{1n}){\rm var}(x_{2n}),\\
c_{25,1}
&\triangleq (1+e_{12})e^{-2k_1h}{\rm var}(\bar{x}_{1n}^2) + (e_{11}-e_{12})e^{-2k_1h}\frac{\sigma_{x1}^2}{k_1}{\rm cm}_3[x_{1n}]\\
&\quad + e^{-k_1h}{\rm cov}(\bar{x}_{1(n+1)}^2,\bar{x}_{1n}\bar{x}_{1(n+1)})\\
&\quad + e_{11}e^{k_1h}{\rm cov}(\bar{x}_{1(n+2)}^2, \bar{x}_{1n}\bar{x}_{1(n+2)}) + (e_{11}e^{k_1h} - e_{12}e^{2k_1h})\frac{\sigma_{x1}^2}{k_1}E[\bar{x}_{1n}\bar{x}_{1(n+2)}^2]\\
&\quad + 2(e_{1,1}e^{-2k_2h} + e^{-2k_2h} + e^{-(k_1+k_2)h} + e_{1,1}e^{2k_2h}){\rm var}(x_{1n}){\rm var}(x_{2n}),\\
c_{26,1}
&\triangleq (1+e_{12})e^{-3k_1h}{\rm var}(\bar{x}_{1n}^2) + (e_{11}-e_{12})e^{-3k_1h}\frac{\sigma_{x1}^2}{k_1}{\rm cm}_3[x_{1n}]\\
&\quad + {\rm cov}(\bar{x}_{1(n+1)}^2,\bar{x}_{1n}\bar{x}_{1(n+3)}) + {\rm cov}(\bar{x}_{1(n+2)}^2,\bar{x}_{1n}\bar{x}_{1(n+3)})\\
&\quad + e_{12}e^{2k_1h}{\rm cov}(\bar{x}_{1(n+3)}^2,\bar{x}_{1n}\bar{x}_{1(n+3)}) + (e_{11}e^{k_1h} - e_{12}e^{2k_1h})\frac{\sigma_{x1}^2}{k_1}E[\bar{x}_{1n}\bar{x}_{1(n+3)}^2]\\
&\quad + 2\left[(1+e_{1,1})e^{-3k_2h} + e^{-(k_1+2k_2)h} + e^{-(2k_1+k_2)h} \right]{\rm var}(x_{1n}){\rm var}(x_{2n})\\
&\quad + 2e_{1,1}e^{(k_2-2k_1)h}{\rm var}(x_{1n}){\rm var}(x_{2n}),\\
\sigma_{34,1}
&\triangleq (1+e_{12})e^{-k_1h}{\rm cov}(\bar{x}_{1n}^3,\bar{x}_{1n}^2) + (e_{11}-e_{12})e^{-k_1h}\frac{\sigma_{x1}^2}{k_1}{\rm cm}_4[x_{1n}]\\
&\quad + e_{13}e^{3k_1h}{\rm cov}(\bar{x}_{1(n+1)}^3,\bar{x}_{1n}\bar{x}_{1(n+1)})\\[1pt]
&\quad + (e_{12}e^{2k_1h}-e_{13}e^{3k_1h})\frac{3\sigma_{x1}^2}{k_1}{\rm cov}(\bar{x}_{1(n+1)}^2,\bar{x}_{1n}\bar{x}_{1(n+1)})\\[1pt]
&\quad + (e_{11}e^{k_1h}-e_{13}e^{3k_1h})\frac{3\sigma_{x1}^2\theta_1}{2k_1}E[\bar{x}_{1n}\bar{x}_{1(n+1)}^2]\\[1pt]
&\quad + (e_{11}e^{k_1h}-2e_{12}e^{2k_1h}+e_{13}e^{3k_1h})\frac{3\sigma_{x1}^4}{2k_1^2} E[\bar{x}_{1n}\bar{x}_{1(n+1)}^2]\\[1pt]
&\quad + 3\left[(1+e_{1,1})e^{-k_2h} + (1+e_{1,1})e^{-k_1h} + e_{2,1}(e^{k_2h}+e^{2k_1h})\right]{\rm cm}_3[x_{1n}]{\rm var}(x_{2n})\\[1pt]
&\quad + 3\left[(e_{1,1}-e_{2,1})e^{k_2h} + (e_{1,1}e^{k_1h} - e_{2,1}e^{2k_1h}) \right]\frac{\sigma_{x1}^2}{k_1}{\rm var}(x_{1n}){\rm var}(x_{2n})\\
&\quad + 3(1+e_{22})e^{-k_2h}{\rm var}(x_{1n}){\rm cm}_3[x_{2n}] + 3(e_{21}-e_{22})e^{-k_2h}\frac{\sigma_{x2}^2}{k_2}{\rm var}(x_{1n}){\rm var}(x_{2n})\\
&\quad + 3e_{21}e^{k_2h}{\rm var}(x_{1n})E[\bar{x}_{2n}\bar{x}_{2(n+1)}^2],\\
c_{35,1}
&\triangleq (1+e_{12})e^{-2k_1h}{\rm cov}(\bar{x}_{1n}^3,\bar{x}_{1n}^2) + (e_{11}-e_{12})e^{-2k_1h}\frac{\sigma_{x1}^2}{k_1}{\rm cm}_4[x_{1n}]\\
&\quad + e^{-k_1h}{\rm cov}(\bar{x}_{1(n+1)}^3,\bar{x}_{1n}\bar{x}_{1(n+1)}) + e_{13}e^{6k_1h}{\rm cov}(\bar{x}_{1(n+2)}^3,\bar{x}_{1n}\bar{x}_{1(n+2)})\\
&\quad + (e_{12}-e_{13})\frac{3\sigma_{x1}^2}{k_1}{\rm cov}(\bar{x}_{1(n+2)}^2,\bar{x}_{1n}\bar{x}_{1(n+2)})
\end{align*}
\begin{align*}
\\[-45pt]
&\quad + \left[(e_{11}-e_{13})\frac{3\sigma_{x1}^2\theta_1}{2k_1} + (e_{11}-2e_{12}+e_{13})\frac{3\sigma_{x1}^4}{2k_1^2} \right]E[\bar{x}_{1n}\bar{x}_{1(n+2)}^2]\\
&\quad + 3(1+e_{1,1})e^{-2k_2h}{\rm cm}_3[x_{1n}]{\rm var}(x_{2n}) + 3E[\bar{x}_{1n}\bar{x}_{1(n+1)}^2]e^{-k_2h}{\rm var}(x_{2n})\\
&\quad + 3e_{2,1}e^{-2k_1h}e^{k_2h}{\rm cm}_3[x_{1n}]{\rm var}(x_{2n})\\
&\quad + 3\left[(1+e_{1,1})e^{-2k_1h} + (e^{-k_1h} + e_{2,1}e^{2k_1h})e^{-k_2h} \right]{\rm cm}_3[x_{1n}]{\rm var}(x_{2n})\\
&\quad + 3(1+e_{22}+e^{-k_2h}+e_{21}e^{-k_2h})e^{-2k_2h}{\rm var}(x_{1n}){\rm cm}_3[x_{2n}]\\
&\quad + 3(e_{1,1}e^{-k_1h}e^{k_2h} - e_{2,1}e^{-2k_1h}e^{k_2h})\frac{\sigma_{x1}^2}{k_1}{\rm var}(x_{1n}){\rm var}(x_{2n})\\
&\quad + 3(e_{1,1}-e_{2,1}e^{k_1h})e^{k_1h}e^{-k_2h}\frac{\sigma_{x1}^2}{k_1}{\rm var}(x_{1n}){\rm var}(x_{2n})\\[1pt]
&\quad + 3\left[ e_{21}-e_{22} + 1 - e^{-k_2h} + e_{21}(e^{k_2h}-e^{-k_2h}) \right]e^{-2k_2h}\frac{\sigma_{x2}^2}{k_2}{\rm var}(x_{1n}){\rm var}(x_{2n}),\\[1pt]
c_{36,1}
&\triangleq (1+e_{12})e^{-3k_1h}{\rm cov}(\bar{x}_{1n}^3,\bar{x}_{1n}^2) + (e_{11}-e_{12})e^{-3k_1h}\frac{\sigma_{x1}^2}{k_1}{\rm cm}_4[x_{1n}]\\[1pt]
&\quad + {\rm cov}(\bar{x}_{1(n+1)}^3,\bar{x}_{1n}\bar{x}_{1(n+3)}) + {\rm cov}(\bar{x}_{1(n+2)}^3,\bar{x}_{1n}\bar{x}_{1(n+3)})\\[1pt]
&\quad + e_{13}e^{3k_1h}{\rm cov}(\bar{x}_{1(n+3)}^3,\bar{x}_{1n}\bar{x}_{1(n+3)})\\[1pt]
&\quad + (e_{12}e^{2k_1h} - e_{13}e^{3k_1h}){\rm cov}(\bar{x}_{1(n+3)}^2,\bar{x}_{1n}\bar{x}_{1(n+3)})\\[1pt]
&\quad + (e_{11}e^{k_1h} - e_{13}e^{3k_1h}){\rm cov}(\bar{x}_{1(n+1)},\bar{x}_{1n}\bar{x}_{1(n+3)})\\[1pt]
&\quad + (e_{11}e^{k_1h} - 2e_{12}e^{2k_1h} + e_{13}e^{3k_1h}) {\rm cov}(\bar{x}_{1(n+1)},\bar{x}_{1n}\bar{x}_{1(n+3)})\\[1pt]
&\quad + 3(1+e_{1,1})e^{-3k_2h}{\rm cm}_3[x_{1n}]{\rm var}(x_{2n})\\[1pt]
&\quad + 3{\rm cov}(\bar{x}_{1(n+1)}^2\bar{x}_{2(n+1)},\bar{x}_{1n}\bar{x}_{2(n+3)}) + 3{\rm cov}(\bar{x}_{1(n+2)}^2\bar{x}_{2(n+2)},\bar{x}_{1n}\bar{x}_{2(n+3)})\\[1pt]
&\quad + 3e_{2,1}e^{-4k_1h}{\rm cm}_3[x_{1n}]{\rm var}(x_{2n}) \\[1pt]
&\quad + 3(e_{1,1}e^{-2k_1h} - e_{2,1}e^{-4k_1h})\frac{\sigma_{x1}^2}{k_1}{\rm var}(x_{1n}){\rm var}(x_{2n})\\[1pt]
&\quad + 3(1+e_{1,1})e^{-3k_1h}{\rm cm}_3[x_{1n}]{\rm var}(x_{2n})\\[1pt]
&\quad + 3{\rm cov}(\bar{x}_{1(n+1)}^2\bar{x}_{2(n+1)},\bar{x}_{2n}\bar{x}_{1(n+3)}) + 3{\rm cov}(\bar{x}_{1(n+2)}^2\bar{x}_{2(n+2)},\bar{x}_{2n}\bar{x}_{1(n+3)})\\[1pt]
&\quad + 3e_{2,1}e^{2k_1h}e^{-2k_2h}{\rm cm}_3[x_{1n}]{\rm var}(x_{2n})\\[1pt]
&\quad + 3(e_{1,1}e^{k_1h}e^{-2k_2h} - e_{2,1}e^{2k_1h}e^{-2k_2h})\frac{\sigma_{x1}^2}{k_1}{\rm var}(x_{1n}){\rm var}(x_{2n})\\[1pt]
&\quad + 3(1+e_{22})e^{-3k_2h}{\rm var}(x_{1n}){\rm cm}_3[x_{2n}]\\[1pt]
&\quad + 3(e_{21}-e_{22})e^{-3k_2h}\frac{\sigma_{x2}^2}{k_2}{\rm var}(x_{1n}){\rm var}(x_{2n})\\[1pt]
&\quad + 3{\rm var}(x_{1n}){\rm cov}(\bar{x}_{2(n+1)},\bar{x}_{2n}\bar{x}_{2(n+3)}) + 3{\rm var}(x_{1n}){\rm cov}(\bar{x}_{2(n+2)},\bar{x}_{2n}\bar{x}_{2(n+3)})\\[1pt]
&\quad + 3e_{21}e^{k_2h}{\rm var}(x_{1n}){\rm cov}(\bar{x}_{2(n+3)},\bar{x}_{2n}\bar{x}_{2(n+3)}),\\
c_{45,1}
&\triangleq e^{-3k_1h}{\rm cm}_4[x_{1n}] + (e^{-2k_1h}-e^{-3k_1h})\frac{\sigma_{x1}^2}{k_1}{\rm cm}_3[x_{1n}] + (e^{-k_1h}-e^{-3k_1h}){\rm var}(x_{1n})\\
&\quad + E[\bar{x}_{1n}\bar{x}_{1(n+1)}\bar{x}_{1(n+2)}^2] - e^{-3k_1h}{\rm var}^2(x_{1n}) + e_{12}{\rm cov}(\bar{x}_{1n}\bar{x}_{1(n+1)},\bar{x}_{1(n+1)}^2)
\end{align*}
\begin{align*}
\\[-35pt]
&\quad + (e_{11}e^{-k_1h}-e_{12})\frac{\sigma_{x1}^2}{k_1}E[\bar{x}_{1n}\bar{x}_{1(n+1)}^2]
+ e_{12}e^{k_1h}{\rm cov}(\bar{x}_{1(n+2)}^2,\bar{x}_{1n}\bar{x}_{1(n+2)})\\[1pt]
&\quad + (e_{11}-e_{12}e^{k_1h})\frac{\sigma_{x1}^2}{k_1}E[\bar{x}_{1n}\bar{x}_{1(n+2)}^2]\\[1pt]
&\quad + \left[(1+e_{1,1})e^{-k_2h} +(1+e_{1,1})e^{-k_1h} \right]{\rm var}(x_{1n}){\rm var}(x_{2n})\\[1pt]
&\quad + \left[e^{-(2k_1+k_2)h} +e^{-(k_1+2k_2)h} \right]{\rm var}(x_{1n}){\rm var}(x_{2n})\\[1pt]
&\quad + e_{1,1}\left[e^{(-2k_1+k_2)h}+e^{(k_1-2k_2)h}\right]{\rm var}(x_{1n}){\rm var}(x_{2n}),\\[1pt]
c_{46,1}
&\triangleq e^{-2k_1h}{\rm var}(\bar{x}_{1n}\bar{x}_{1(n+1)}) + e_{12}e^{-k_1h}{\rm cov}(\bar{x}_{1n}\bar{x}_{1(n+1)},\bar{x}_{1(n+1)}^2)\\
&\quad + (e_{11}e^{k_1h} - e_{12}e^{2k_1h})e^{-3k_1h}\frac{\sigma_{x1}^2}{k_1}{\rm cov}(\bar{x}_{1n}\bar{x}_{1(n+1)},\bar{x}_{1(n+1)})\\
&\quad + {\rm cov}(\bar{x}_{1(n+1)}\bar{x}_{1(n+2)},\bar{x}_{1n}\bar{x}_{1(n+3)}) + {\rm cov}(\bar{x}_{1(n+2)}\bar{x}_{1(n+3)},\bar{x}_{1n}\bar{x}_{1(n+3)})\\
&\quad + e_{12}e^{k_1h}{\rm cov}(\bar{x}_{1(n+3)}^2,\bar{x}_{1n}\bar{x}_{1(n+3)}) \\
&\quad + (e_{11}e^{k_1h}-e_{12}e^{2k_1h})e^{-k_1h}\frac{\sigma_{x1}^2}{k_1}{\rm cov}(\bar{x}_{1(n+3)},\bar{x}_{1n}\bar{x}_{1(n+3)})\\
&\quad + (1+e_{1,1})e^{-2k_2h}{\rm var}(x_{1n}){\rm var}(x_{2n}) + e^{-k_1h}e^{-k_2h}{\rm var}(x_{1n}){\rm var}(x_{2n})\\
&\quad + e_{1,1}e^{-k_1h}e^{k_2h}{\rm var}(x_{1n}){\rm var}(x_{2n})\\
&\quad + e^{-3k_1h}e^{-k_2h}{\rm var}(x_{1n}){\rm var}(x_{2n}) + e_{1,1}e^{-3k_1h}e^{k_2h}{\rm var}(x_{1n}){\rm var}(x_{2n})\\
&\quad + \left[ e^{-2(k_1+k_2)h} + e^{-(k_1+3k_2)h} + e_{1,1}e^{(k_1-3k_2)h} \right]{\rm var}(x_{1n}){\rm var}(x_{2n}),\\
c_{56,1}
&\triangleq e^{-k_1h}{\rm var}(\bar{x}_{1n}\bar{x}_{1(n+2)}) + {\rm cov}(\bar{x}_{1n}\bar{x}_{1(n+2)},\bar{x}_{1(n+1)}\bar{x}_{1(n+4)})\\
&\quad + e_{12}e^{-k_1h}{\rm cov}(\bar{x}_{1n}\bar{x}_{1(n+2)},\bar{x}_{1(n+2)}^2)\\
&\quad + (e_{11}e^{k_1h}-e_{12}e^{2k_1h})e^{-3k_1h}\frac{\sigma_{x1}^2}{k_1}{\rm cov}(\bar{x}_{1n}\bar{x}_{1(n+2)},\bar{x}_{1(n+2)})\\
&\quad + {\rm cov}(\bar{x}_{1(n+1)}\bar{x}_{1(n+3)},\bar{x}_{1n}\bar{x}_{1(n+3)}) + {\rm cov}(\bar{x}_{1(n+2)}\bar{x}_{1(n+4)},\bar{x}_{1n}\bar{x}_{1(n+3)})\\
&\quad + e_{12}{\rm cov}(\bar{x}_{1(n+3)}^2,\bar{x}_{1n}\bar{x}_{1(n+3)})\\
&\quad + (e_{11}e^{k_1h} - e_{12}e^{2k_2h})e^{-2k_1h}\frac{\sigma_{x1}^2}{k_1}{\rm cov}(\bar{x}_{1(n+3)},\bar{x}_{1n}\bar{x}_{1(n+3)})\\
&\quad + (1+e_{1,1})e^{-k_2h}{\rm var}(x_{1n}){\rm var}(x_{2n}) + e_{1,1}e^{k_2h}{\rm var}(x_{1n}){\rm var}(x_{2n})\\
&\quad + \left[e^{-3k_1h}e^{-2k_1h} + e^{-(3k_1+k_2)h} + e_{1,1}e^{-4k_1h}e^{k_2h} \right]{\rm var}(x_{1n}){\rm var}(x_{2n})\\
&\quad + \left[ e^{-2k_1h}e^{-3k_2h} + e^{-k_1h}e^{-4k_2h} + e_{1,1}e^{k_1h}e^{-4k_2h}\right]{\rm var}(x_{1n}){\rm var}(x_{2n}).
\end{align*}
Open access
