No CrossRef data available.
Article contents
Lost sales obsolescence inventory systems with positive lead time: a system-point level-crossing approach
Published online by Cambridge University Press: 26 May 2022
Abstract
In this article, we provide a comprehensive analyses of two continuous review lost sales inventory system based on different replenishment policies, namely 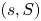 $(s,S)$ and
$(s,S)$ and 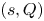 $(s,Q)$. We assume that the arrival times of demands form a Poisson process and that the demand sizes have i.i.d. exponential distribution. We assume that the items in stock may obsolete after an exponential time. The lead time for replenishment is exponential. We also assume that the excess demands and the demands that occurred during stock out periods are lost. Using the system point method of level crossing and integral equation method, we derive the steady-state probability distribution of inventory level explicitly. After deriving some system performance measures, we computed the total expected cost rate. We also provide numerical examples of sensitivity analyses involving different parameters and costs. As a result of our numerical analysis, we provide several insights on the optimal
$(s,Q)$. We assume that the arrival times of demands form a Poisson process and that the demand sizes have i.i.d. exponential distribution. We assume that the items in stock may obsolete after an exponential time. The lead time for replenishment is exponential. We also assume that the excess demands and the demands that occurred during stock out periods are lost. Using the system point method of level crossing and integral equation method, we derive the steady-state probability distribution of inventory level explicitly. After deriving some system performance measures, we computed the total expected cost rate. We also provide numerical examples of sensitivity analyses involving different parameters and costs. As a result of our numerical analysis, we provide several insights on the optimal 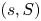 $(s,S)$ and
$(s,S)$ and 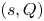 $(s,Q)$ policies for inventory systems of obsolescence items with positive lead times. The better policy for maintaining inventory can be quantified numerically.
$(s,Q)$ policies for inventory systems of obsolescence items with positive lead times. The better policy for maintaining inventory can be quantified numerically.
Keywords
- Type
- Research Article
- Information
- Probability in the Engineering and Informational Sciences , Volume 37 , Issue 3 , July 2023 , pp. 778 - 800
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press


