Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T09:39:56.613Z Has data issue: false hasContentIssue false
  • English
  • Français

EXACT ASYMPTOTICS OF SAMPLE-MEAN-RELATED RARE-EVENT PROBABILITIES

Published online by Cambridge University Press:  16 January 2017

Julia Kuhn Open the ORCID record for Julia Kuhn [Opens in a new window] ,
Michel Mandjes  and
Thomas Taimre
Julia Kuhn
Affiliation:
Korteweg-de Vries Institute for Mathematics, University of Amsterdam, Science Park 105, 1098 XH Amsterdam, The Netherlands School of Mathematics and Physics, The University of Queensland, St. Lucia, QLD 4072, Australia E-mail: [email protected]
Michel Mandjes
Affiliation:
Korteweg-de Vries Institute for Mathematics, University of Amsterdam, Science Park 105, 1098 XH Amsterdam, The Netherlands E-mail: [email protected]
Thomas Taimre
Affiliation:
School of Mathematics and Physics, The University of Queensland, St. Lucia, QLD 4072, Australia E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Relying only on the classical Bahadur–Rao approximation for large deviations (LDs) of univariate sample means, we derive strong LD approximations for probabilities involving two sets of sample means. The main result concerns the exact asymptotics (as n→∞) of

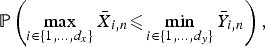$$ {\open P}\left({\max_{i\in\{1,\ldots,d_x\}}\bar X_{i,n} \les \min_{i\in\{1,\ldots,d_y\}}\bar Y_{i,n}}\right),$$
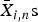with the ${\bar X}_{i,n}{\rm s}$ (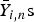${\bar Y}_{i,n}{\rm s}$, respectively) denoting dx (dy) independent copies of sample means associated with the random variable X (Y). Assuming 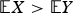${\open E}X \gt {\open E}Y$ , this is a rare event probability that vanishes essentially exponentially, but with an additional polynomial term. We also point out how the probability of interest can be estimated using importance sampling in a logarithmically efficient way. To demonstrate the usefulness of the result, we show how it can be applied to compare the order statistics of the sample means of the two populations. This has various applications, for instance in queuing or packing problems.

Keywords

applied probabilityoperations researchstochastic dynamic programmingstochastic modeling
Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 32 , Issue 2 , April 2018 , pp. 207 - 228
Copyright
Copyright © Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Andriani, C. & Baldi, P. (1997). Sharp estimates of deviations of the sample mean in many dimensions. Annales de l'Institut Henri Poincare (B) Probability and Statistics 33(3): 371–385.CrossRefGoogle Scholar
2. Asmussen, S. & Glynn, P.W. (2007). Stochastic simulation: algorithms and analysis. Stochastic Modelling and Applied Probability. New York: Springer.CrossRefGoogle Scholar
3. Bahadur, R.R. & Rao, R.R. (1960). On deviations of the sample mean. The Annals of Mathematical Statistics 31(4): 1015–1027.CrossRefGoogle Scholar
4. Chaganty, N.R. (1997). Large deviations for joint distributions and statistical applications. Sankhyā: The Indian Journal of Statistics, Series A 59: 147–166.Google Scholar
5. Chaganty, N.R. & Sethuraman, J. (1993). Strong large deviation and local limit theorems. The Annals of Probability 21(3): 1671–1690.Google Scholar
6. Chaganty, N.R. & Sethuraman, J. (1996). Multidimensional strong large deviation theorems. Journal of Statistical Planning and Inference 55(3): 265–280.CrossRefGoogle Scholar
7. Dembo, A. & Zeitouni, O. (1998). Large deviations techniques and applications, 2nd ed. New York: Springer-Verlag.Google Scholar
8. Glynn, P. & Juneja, S. (2004). A large deviations perspective on ordinal optimization. In Proceedings of the 2004 Winter Simulation Conference. Vol. 1, IEEE.Google Scholar
9. Glynn, P. & Juneja, S. (2015). Ordinal optimization-empirical large deviations rate estimators, and stochastic multi-armed bandits. arXiv preprint arXiv:1507.04564.Google Scholar
10. Höglund, T. (1979). A unified formulation of the central limit theorem for small and large deviations from the mean. Zeitschrift für Wahrscheinlichkeitstheorie und verwandte Gebiete 49(1): 105–117.Google Scholar
11. Iltis, M. (1995). Sharp asymptotics of large deviations in ℝ d . Journal of Theoretical Probability 8(3): 501–522.Google Scholar
12. Mandjes, M. (2007). Large deviations for Gaussian queues. Chichester, UK: John Wiley & Sons, Ltd,.Google Scholar
13. Petrov, V.V. (1975). Sums of independent random variables. New York: Springer-Verlag.Google Scholar
14. Sadowsky, J.S. & Bucklew, J.A. (1990). On large deviations theory and asymptotically efficient Monte Carlo estimation. IEEE Transactions on Information Theory 36(3): 579–588.Google Scholar