No CrossRef data available.
Article contents
Chi-Square Goodness of Fit: A Failure Rate Perspective
Published online by Cambridge University Press: 27 July 2009
Abstract
Employing a failure rate approach, we propose a test statistic, 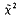 , for the classic goodness-of-fit problem. It is then shown that a variation of
, for the classic goodness-of-fit problem. It is then shown that a variation of 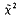 , obtained by replacing observed variances by expected variances (an unwise change in our point of view), leads to the classical test statistic, x2. We argue that
, obtained by replacing observed variances by expected variances (an unwise change in our point of view), leads to the classical test statistic, x2. We argue that 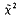 should be better approximated by a chi-square distribution, and thus employing
should be better approximated by a chi-square distribution, and thus employing 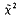 , the true p−values should be closer to the nominal p−values than under x2 Various other comparisons of the two tests are made.
, the true p−values should be closer to the nominal p−values than under x2 Various other comparisons of the two tests are made.
- Type
- Articles
- Information
- Probability in the Engineering and Informational Sciences , Volume 5 , Issue 3 , July 1991 , pp. 273 - 284
- Copyright
- Copyright © Cambridge University Press 1991


