Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Angus, John E.
1995.
A Coupling Proof of the Asymptotic Normality of the Permutation Oscillation.
Probability in the Engineering and Informational Sciences,
Vol. 9,
Issue. 4,
p.
615.
Chao, Chern-Ching
Zhao, Lincheng
and
Liang, Wen-Qi
1996.
Estimating the Error of a Permutational Central Limit Theorem.
Probability in the Engineering and Informational Sciences,
Vol. 10,
Issue. 4,
p.
533.
Chatterjee, Sourav
2021.
A New Coefficient of Correlation.
Journal of the American Statistical Association,
Vol. 116,
Issue. 536,
p.
2009.
Shi, H
Drton, M
and
Han, F
2022.
On the power of Chatterjee’s rank correlation.
Biometrika,
Vol. 109,
Issue. 2,
p.
317.
Sadeghi, Behnam
2022.
Chatterjee Correlation Coefficient: A robust alternative for classic correlation methods in geochemical studies- (including “TripleCpy” Python package).
Ore Geology Reviews,
Vol. 146,
Issue. ,
p.
104954.
Xia, Liqi
Cao, Ruiyuan
Du, Jiang
and
Chen, Xiuping
2024.
The improved correlation coefficient of Chatterjee.
Journal of Nonparametric Statistics,
p.
1.


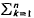 | π
| π