Article contents
ASYMPTOTIC ANALYSIS OF OPTIMAL NESTED GROUP-TESTING PROCEDURES
Published online by Cambridge University Press: 29 June 2016
Abstract
We analyze a construction for optimal nested group-testing procedures, and show that, when individuals are independently positive with probability p, the expected number of tests per positive individual, F*(p), has, as p→0, the asymptotic behavior
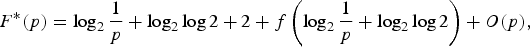 $$F^{\ast}(p) = \log_2 {1\over p} + \log_2 \log 2 + 2 + f\left(\log_2 {1\over p} + \log_2 \log 2\right) + O(p),$$
$$F^{\ast}(p) = \log_2 {1\over p} + \log_2 \log 2 + 2 + f\left(\log_2 {1\over p} + \log_2 \log 2\right) + O(p),$$ $$f(z) = 4\times 2^{-2^{1-\{z\}}} - \{z\} - 1,$$
$$f(z) = 4\times 2^{-2^{1-\{z\}}} - \{z\} - 1,$$
- Type
- Research Article
- Information
- Probability in the Engineering and Informational Sciences , Volume 30 , Issue 4 , October 2016 , pp. 547 - 552
- Copyright
- Copyright © Cambridge University Press 2016
References
- 8
- Cited by


