Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-22T21:34:35.908Z Has data issue: false hasContentIssue false
  • English
  • Français

APPROXIMATING AND STABILIZING DYNAMIC RATE JACKSON NETWORKS WITH ABANDONMENT

Published online by Cambridge University Press:  03 January 2017

Jamol Pender  and
William A. Massey
Jamol Pender
Affiliation:
School of Operations Research and Information Engineering, Cornell University, Ithaca, New York, USA E-mail: [email protected]
William A. Massey
Affiliation:
Department of Operations Research and Financial Engineering, Princeton University, Princeton, New Jersey, USA E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we generalize the Gaussian Variance Approximation (GVA), developed by Massey and Pender [16], to Jackson networks with abandonment. We approximate the queue length process with a multivariate Gaussian distribution and thus, we are able to estimate the mean and covariance matrix of the entire network with more accuracy than the associated fluid and diffusion limits of Mandelbaum, Massey, and Reiman [14]. We also show how the GVA method can be used to construct staffing schedules that approximately stabilize salient performance measures such as the probability of delay and the abandonment probabilities for the entire network. Unlike the work of Feldman et al. [5] which uses Monte Carlo simulation to stabilize the delay probabilities, our method does not require simulation and only requires the numerical integration of 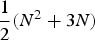${1 \over 2}(N^2 + 3N)$ differential equations for an N-dimensional network, which is more computationally efficient. Lastly, to confirm our approximations are accurate, we perform several numerical experiments for a wide range of parameter settings.

Keywords

Queueing TheoryApplied ProbabilityComputational ProbabilitySimulationProbabilistic NetworksStochastic Modeling
Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 31 , Issue 1 , January 2017 , pp. 1 - 42
Copyright
Copyright © Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Cameron, R.H. & Martin, W.T. (1947). The orthogonal development of non-linear functionals in series of Fourier-Hermite functionals. Annals of Mathematics 385–392.Google Scholar
2. Defraeye, M. & Van Nieuwenhuyse, I. (2016). Staffing and scheduling under nonstationary demand for service: A literature review. Omega 58: 4–25.CrossRefGoogle Scholar
3. Dong, J., Feldman, P., & Yom-Tov, G. (2013). Slowdown services: Staffing service systems with load-dependent service rate. Available at SSRN 2317410.Google Scholar
4. Engblom, S. & Pender, J. (2014). Approximations for the moments of nonstationary and state dependent birth-death queues. Arxiv preprint arXiv:1406.6164.Google Scholar
5. Feldman, Z., Mandelbaum, A., Massey, W.A., & Whitt, W. (2008). Staffing of time-varying queues to achieve time-stable performance. Management Science 54(2): 324–338.Google Scholar
6. Jennings, O.B., Mandelbaum, A., Massey, W.A., & Whitt, W. (1996). Server staffing to meet time-varying demand. Management Science 42(10): 1383–1394.Google Scholar
7. Khudyakov, P., Feigin, P.D., & Mandelbaum, A. (2010). Designing a call center with an IVR (interactive voice response). Queueing Systems 66(3): 215–237.CrossRefGoogle Scholar
8. Ko, Y.M. & Gautam, N. (2013). Critically loaded time-varying multiserver queues: computational challenges and approximations. INFORMS Journal on Computing 25(2): 285–301.CrossRefGoogle Scholar
9. Ko, Y.M. & Pender, J. Diffusion limits for the (map(t)/ph(t)/) n queueing network.Google Scholar
10. Ko, Y.M. & Pender, J. Strong approximations for time varying infinite-server queues with non-renewal arrival and service processes.Google Scholar
11. Liu, Y. & Whitt, W. Stabilizing performance in a service system with time-varying arrivals and customer feedback. Technical Report., Working paper.Google Scholar
12. Liu, Y. & Whitt, W. (2012). Stabilizing customer abandonment in many-server queues with time-varying arrivals. Operations Research 60(6): 1551–1564.Google Scholar
13. Liu, Y. & Whitt, W. (2014). Stabilizing performance in networks of queues with time-varying arrival rates. Probability in the Engineering and Informational Sciences 28(04): 419–449.Google Scholar
14. Mandelbaum, A., Massey, W.A., & Reiman, M.I. (1998). Strong approximations for Markovian service networks. Queueing Systems 30 (1–2): 149–201.Google Scholar
15. Mandelbaum, A., Massey, W.A., Reiman, M.I., Stolyar, A., & Rider, B. (2002). Queue lengths and waiting times for multiserver queues with abandonment and retrials. Telecommunication Systems 21 (2–4): 149–171.Google Scholar
16. Massey, W. & Pender, J. (2011). Skewness variance approximation for dynamic rate multi-server queues with abandonment. Performance Evaluation Review 39: 74–74.Google Scholar
17. Massey, W. & Pender, J. (2013). Gaussian skewness approximation for dynamic rate multi-server queues with abandonment. Queueing Systems 75(2): 243–277.CrossRefGoogle Scholar
18. Massey, W.A. & Whitt, W. (1993). Networks of infinite-server queues with nonstationary poisson input. Queueing Systems 13 (1–3): 183–250.Google Scholar
19. Pender, J. Time varying queues with abandonment via Laguerre polynomial expansions. Technical report., Cornell University, Cornell University.Google Scholar
20. Pender, J. (2014). Gram charlier expansion for time varying multiserver queues with abandonment. SIAM Journal on Applied Mathematics 74(4): 1238–1265.CrossRefGoogle Scholar
21. Pender, J. (2014). A Poisson–Charlier approximation for nonstationary queues. Operations Research Letters 42(4): 293–298.Google Scholar
22. Pender, J. (2016). An analysis of nonstationary coupled queues. Telecommunication Systems 61(4): 823–838.CrossRefGoogle Scholar
23. Pender, J. (2015). Nonstationary loss queues via cumulant moment approximations. Probability in the Engineering and Informational Sciences 29(01): 27–49.CrossRefGoogle Scholar
24. Pender, J. & Ko, Y.M. Approximations for the queue length distributions of time-varying many-server queues.Google Scholar
25. Pender, J. & Phung-Duc, T. (2016). A law of large numbers for M/M/c/delayo-setup queues with nonstationary arrivals. In Analytical and Stochastic Modelling Techniques and Applications: 23rd International Conference Proceedings, Cardiff, UK, 24–26 August, 2016, vol. 9845, Springer.Google Scholar
26. Ross, S.M. (2006). Simulation. Amsterdam: Elsevier Academic Press.Google Scholar
27. Stein, C. (1986). Approximate computation of expectations. Lecture Notes-Monograph Series 7: i–164.Google Scholar
28. Véricourt, F.d. & Jennings, O.B. (2011). Nurse staffing in medical units: A queueing perspective. Operations Research 59(6): 1320–1331.CrossRefGoogle Scholar
29. Wiener, N. (1938). The homogeneous chaos. American Journal of Mathematics 60(4): 897–936.Google Scholar
30. Xiu, D., & Karniadakis, G.E. (2002). The Wiener–Askey polynomial chaos for stochastic differential equations. SIAM Journal on Scientific Computing 24(2): 619–644.Google Scholar
31. Yom-Tov, G.B. & Mandelbaum, A. (2014). Erlang-r: A time-varying queue with reentrant customers, in support of healthcare staffing. Manufacturing & Service Operations Management 16(2): 283–299.Google Scholar