Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-22T19:12:10.477Z Has data issue: false hasContentIssue false
  • English
  • Français

AGING FUNCTIONS AND MULTIVARIATE NOTIONS OF NBU AND IFR

Published online by Cambridge University Press:  18 March 2010

Fabrizio Durante ,
Rachele Foschi  and
Fabio Spizzichino
Fabrizio Durante
Affiliation:
Department of Knowledge-Based Mathematical Systems, Johannes Kepler UniversityA-4040 Linz, Austria E-mail: [email protected]
Rachele Foschi
Affiliation:
Dipartimento di Matematica, University “La Sapienza”I-00185 Rome, Italy E-mail: [email protected], [email protected]
Fabio Spizzichino
Affiliation:
Dipartimento di Matematica, University “La Sapienza”I-00185 Rome, Italy E-mail: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

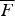For d≥2, let X=(X1, …, Xd) be a vector of exchangeable continuous lifetimes with joint survival function . For such models, we study some properties of multivariate aging of 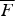that are described by means of the multivariate aging function 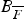, which is a useful tool for describing the level curves of 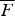. Specifically, the attention is devoted to notions that generalize the univariate concepts of New Better than Used and Increasing Failure Rate. These multivariate notions are satisfied by random vectors whose components are conditionally independent and identically distributed having univariate conditional survival function that is New Better than Used (respectively, Increasing Failure Rate). Furthermore, they also have an interpretation in terms of comparisons among conditional survival functions of residual lifetimes, given a same history of observed survivals.

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 24 , Issue 2 , April 2010 , pp. 263 - 278
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Avérous, J. & Dortet-Bernadet, J.-L. (2004). Dependence for Archimedean copulas and aging properties of their generating functions. Sankhyā 66(4): 607–620.Google Scholar
2.Barlow, R.E. & Mendel, M.B. (1992). de Finetti-type representations for life distributions. Journal of the Amercian Statistical Association 87(420): 1116–1122.CrossRefGoogle Scholar
3.Barlow, R.E. & Spizzichino, F. (1993). Schur-concave survival functions and survival analysis. Journal Computational and Applied Mathematics, 46(3): 437–447.Google Scholar
4.Bassan, B. & Spizzichino, F. (1999). Stochastic comparisons for residual lifetimes and Bayesian notions of multivariate ageing. Advances in Applied Probablity 31(4): 1078–1094.CrossRefGoogle Scholar
5.Bassan, B. & Spizzichino, F. (2000). On a multivariate notion of New Better than Used. In 2nd International Conference of Mathematical Methods of Reliability Theory, Bordeaux, France, pp. 167–169.Google Scholar
6.Bassan, B. & Spizzichino, F. (2001). Dependence and multivariate aging: The role of level sets of the survival function. System and Bayesian reliability. World Scientific Publishing, River Edge, NJ: pp. 229–242.Google Scholar
7.Bassan, B. & Spizzichino, F. (2003). On some properties of dependence and aging for residual lifetimes in the exchangeable case. Mathematical and statistical methods in reliability World Scientific Publishing, River Edge, NJ: pp. 235–249.CrossRefGoogle Scholar
8.Bassan, B. & Spizzichino, F. (2005). Bivariate survival models with Clayton aging functions. Insurance: 37(1): 6–12.Google Scholar
9.Bassan, B. & Spizzichino, F. (2005). Relations among univariate aging, bivariate aging and dependence for exchangeable lifetimes. Journal of Multivariate Analysis 93(2): 313–339.CrossRefGoogle Scholar
10.Durante, F., Foschi, R. & Sarkoci, P. (2010). Distorted copulas: Constructions and tail dependence. Communications in Statistics: Theory and Methods.Google Scholar
11.Durante, F. & Ghiselli-Ricci, R. (2009). Supermigrative semi-copulas and triangular norms. Information Sciences 179(15): 2689–2694.CrossRefGoogle Scholar
12.Durante, F., Hofert, M. & Scherer, M. (2010). Multivariate hierarchical copulas with shocks. Methodology and Computing in Applied Probablity.Google Scholar
13.Durante, F., Quesada-Molina, J.J. & Úbeda-Flores, M. (2007). On a family of multivariate copulas for aggregation processes. Information Sciences 177(24): 5715–5724.CrossRefGoogle Scholar
14.Durante, F. & Sempi, C. (2005). Copula and semicopula transforms. International Journal of Mathematics and Mathematical Sciences 2005(4): 645–655.CrossRefGoogle Scholar
15.Durante, F. & Sempi, C. (2005). Semicopulæ. Kybernetika (Prague) 41(3): 315–328.Google Scholar
16.Durante, F. & Spizzichino, F. (2010). Semi-copulas, capacities and families of level curves. Fuzzy Sets and Systems 161: 269–276.CrossRefGoogle Scholar
17.Foschi, R. (2009). Semigroups of semi-copulas and a general approach to hyper-dependence properties. Preprint.Google Scholar
18.Foschi, R. & Spizzichino, F. (2008). Semigroups of semicopulas and evolution of dependence at increase of age. Mathware & Soft Computing XV(1): 95–111.Google Scholar
19.Joe, H. (1997). Multivariate models and dependence concepts. London: Chapman & Hall.Google Scholar
20.Klement, E.P., Mesiar, R. & Pap, E. (2000). Triangular norms, Dordrecht: Kluwer Academic.Google Scholar
21.Klement, E.P., Mesiar, R. & Pap, E. (2005). Transformations of copulas. Kybernetika (Prague) 41(4): 425–434.Google Scholar
22.Lai, C.-D. & Xie, M. (2006). Stochastic ageing and dependence for reliability. New York: Springer.Google Scholar
23.Marshall, A.W. & Olkin, I. (1979). Inequalities: Theory of majorization and its applications. New York: Academic Press.Google Scholar
24.Mc Neil, A.J., & Nešlehová, J. (2009). Multivariate Archimedean copulas, d-monotone functions and ℓ1-norm symmetric distributions. Annals of Statistics 37(5B): 3059–3097.Google Scholar
25.Nelsen, R.B. (2006). An introduction to copulas, 2nd ed.New York: Springer.Google Scholar
26.Shaked, M. & Shanthikumar, J.G. (2007). Stochastic orders. New York: Springer.Google Scholar
27.Sklar, A. (1959). Fonctions de répartition à n dimensions et leurs marges. Publications de l'Institut de Statistique de l'Université de Paris 8: 229–231.Google Scholar
28.Spizzichino, F. (1992). Reliability decision problems under conditions of aging. In Bernando, J., Berger, J., Dawid, A.P. & Smith, A.F.M., (eds.) Proceedings of the Fourth International Meeting on Bayesian Statistics. Oxford: Clarendon Press, pp. 803–811.CrossRefGoogle Scholar
29.Spizzichino, F. (2001). Subjective probability models for lifetimes. Boca Raton, FL: Chapman & Hall/CRC.CrossRefGoogle Scholar