Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-20T00:50:47.139Z Has data issue: false hasContentIssue false
  • English
  • Français

A Versatile Packet Arrival Process and Its Second Order Properties

Published online by Cambridge University Press:  27 July 2009

Teunis J. Ott
Teunis J. Ott
Affiliation:
Bellcore, 445 South Street, Morristown, New Jersey 07960
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we describe a class of discrete time processes 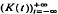that can be used to model packet arrival streams in packetized communication. Mathematically, (K(t)) can be seen as a discrete time self-exciting point process, as a multitype branching process, or as an epidemic with immigration of infected people. The purpose of this paper is to show that this class of models simultaneously is quite useful and analytically more tractable than is obvious at first glance. It is shown that certain probabilities can reliably be computed using generating function methods, and expressions are given for the second order properties and for the asymptotic index of dispersion.

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 7 , Issue 4 , October 1993 , pp. 495 - 513
Copyright
Copyright © Cambridge University Press 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Anick, D., Mitra, D., & Sondhi, M.M. (1982). Stochastic theory of a data handling system. Bell System Technical Journal 61: 1871–1894.CrossRefGoogle Scholar
2.Athreya, K.B. & Ney, P.E. (1972). Branching processes. New York: Springer-Verlag.CrossRefGoogle Scholar
3.Daigle, J.N. & Langford, J.D. (1986). Models for analysis of packet voice communications systems. IEEE Journal of Select Areas of Communications 4: 847–855.CrossRefGoogle Scholar
4.Hawkes, A.G. & Oakes, D. (1974). A cluster point representation of a self-exciting process. Journal of Applied Probability 11: 493–503.CrossRefGoogle Scholar
5.Heffes, H. & Lucantoni, D.M. (1986). A Markov modulated characterization of packetized voice and data traffic and related statistical multiplexer performance. IEEE Journal of Select Areas of Communications SAC-4: 856–868.CrossRefGoogle Scholar
6.Kosten, L. (1974). Stochastic theory of a multi-entry buffer, I, II. Delft Progress Report Series F: Mathematical Engineering, Mathematics and Information Engineering 1: 16–18, 44–50.Google Scholar
7.Kosten, L. & Vrieze, O. (1975). Stochastic theory of a multi-entry buffer III. Delft Progress Report Series F: Mathematical Engineering, Mathematics and Information Engineering I: 103–115.Google Scholar
8.Ott, T.J. (1991). Spectral analysis of point processes with special attention to processes occurring in packetized communication. Bellcore Internal Publication, Morristown, NJ.Google Scholar
9.Ott, T.J. (1993). A queuing system with a branching process arrival stream, the case of short-range dependence. Probability in the Engineering and Informational Sciences 7: 515–528.CrossRefGoogle Scholar
10.Ott, T.J. (1993). A queuing system with a branching process arrival stream, the case of intermediate-range dependence. Bellcore Internal Publication, Morristown, NJ.Google Scholar
11.Ott, T.J. & Shanthikumar, G. (1991). On a buffer problem for packetized voice with an N-periodic strongly interchangeable input process. Journal of Applied Probability 28: 630–646.CrossRefGoogle Scholar
12.Ramaswami, V. & Latouche, G. (1988). Modeling packet arrivals form asynchronous input lines. Proceedings of ITC, paper 4.1.A.5.Google Scholar
13.Sengupta, B. (1990). A queue with superposition of arrival streams with an application to packet voice technology. In King, P.J.B., Mitrami, I., & Pouley, R.J. (eds.) Proceedings of PERFORMANCE '90. Amsterdam: North-Holland.Google Scholar
14.Snyder, D.L. (1975). Random point processes. New York: Wiley Interscience.Google Scholar
15.Sriram, K. & Whitt, W. (1986). Characterizing superposition arrival processes in packet multiplexers for voice and data. IEEE Journal of Select Areas of Communications SAC-4: 833–846.CrossRefGoogle Scholar
16.Van Doom, E.A., Jagers, A.A., & de Wit, J.S.J. (1988). A fluid reservoir regulated by a birth-death process. Communication Statistics—Stochastic Models 4(3): 457–472.CrossRefGoogle Scholar