Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T13:40:32.575Z Has data issue: false hasContentIssue false
  • English
  • Français

Team's seasonal win probabilities

Published online by Cambridge University Press:  02 July 2021

Sheldon M. Ross Open the ORCID record for Sheldon M. Ross [Opens in a new window]
Sheldon M. Ross*
Affiliation:
Department of Industrial and Systems Engineering, University of Southern California, Los Angeles, CA 90089, USA. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a competition involving 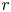$r$ teams, where each individual game involves two teams, and where each game between teams 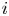$i$ and 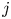$j$ is won by 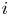$i$ with probability 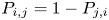$P_{i,j} = 1 - P_{j,i}$. We suppose that 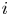$i$ and 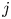$j$ are scheduled to play 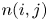$n(i,j)$ games and say that the team that wins the most games is the winner of the competition. We show that the conditional probability that 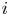$i$ is the winner, given that 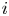$i$ wins 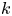$k$ games, is increasing in 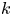$k$. We bound the tail probability of the number of wins of the winning team. We consider the special case where 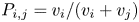$P_{i,j} = {v_i}/{(v_i + v_j)}$, and obtain structural results on the probability that team 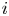$i$ is the winner. We give efficient simulation approaches for computing the probability that team 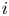$i$ is the winner, and the conditional probability given the number of wins of 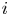$i$.

Keywords

Applied probabilitySimulationStochastic modeling
Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 36 , Issue 4 , October 2022 , pp. 988 - 998
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, I., Cao, Y., Karp, R.M., Pekoz, E., & Ross, S.M. (2017). Random knockout tournaments. Operations Research 65(6): 1589–1596.CrossRefGoogle Scholar
Cao, Y. & Ross, S.M. (2019). Winner plays structure in random knockout tournaments. Probability in the Engineering and Informational Sciences 33(4): 500–510.CrossRefGoogle Scholar
Chung, F.R.K. & Hwang, F.K. (1978). Do stronger players win more knockout tournaments? Journal of the American Statistical Association 73(363): 593–596.CrossRefGoogle Scholar
David, H.A. (1959). Tournaments and paired comparisons. Biometrika 46(1/2): 139–149.CrossRefGoogle Scholar
Edwards, T.E. (1996). Double-elimination tournaments: counting and calculating. The American Statistician 50(1): 27–33.Google Scholar
Glenn, W.A. (1960). A comparison of the effectiveness of tournaments. Biometrika 47(3/4): 253–262.CrossRefGoogle Scholar
Hennessy, J. & Glickman, M. (2016). Bayesian optimal design of fixed knockout tournament brackets. Journal of Quantitative Analysis in Sports 12(1): 1–15.CrossRefGoogle Scholar
Horen, J. & Riezman, R. (1985). Comparing draws for single elimination tournaments. Operations Research 33(2): 249–262.CrossRefGoogle Scholar
Hwang, F.K. (1982). New concepts in seeding knockout tournaments. The American Mathematical Monthly 89(4): 235–239.CrossRefGoogle Scholar
Marchand, E. (2002). On the comparison between standard and random knockout tournaments. Journal of the Royal Statistical Society: Series D (The Statistician) 51(2): 169–178.Google Scholar
Marshall, A. & Olkin, I. (1979). Inequalities: theory of majorization and its applications. New York, USA: Academic Press.Google Scholar
Maurer, W. (1975). On most effective tournament plans with fewer games than competitors. The Annals of Statistics 3(3): 717–727.CrossRefGoogle Scholar
Moser, L. & Harary, F. (1966). The theory of round robin tournaments. The American Mathematical Monthly 73(3): 231–246.Google Scholar
Pekoz, E. & Ross, S.M. (2007). A second course in probability. Berkeley, USA: Probability/Bookstore.com.Google Scholar
Ross, S.M. (2013). Simulation, 5th ed. San Diego, USA: Academic Press.Google ScholarPubMed
Ross, S.M. (2016). Improved Chen-Stein bounds on the probability of a union. Journal of Applied Probability 53(4): 1265–1270.CrossRefGoogle Scholar
Saarinen, S., Tovey, C.A., & Goldsmith, J. (2014). A model for intransitive preferences. Presented at Meeting of Association for Advancement of Artificial Intelligence.Google Scholar
Searls, D.T. (1963). On the probability of winning with different tournament procedures. Journal of the American Statistical Association 58(304): 1064–1081.CrossRefGoogle Scholar