Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-18T06:23:14.302Z Has data issue: false hasContentIssue false
  • English
  • Français

STOCHASTIC COMPARISONS OF PARALLEL SYSTEMS WHEN COMPONENTS HAVE PROPORTIONAL HAZARD RATES

Published online by Cambridge University Press:  22 October 2007

Subhash Kochar  and
Maochao Xu
Subhash Kochar
Affiliation:
Department of Mathematics and StatisticsPortland State UniversityPortland, OR 97201 E-mail: [email protected]
Maochao Xu
Affiliation:
Department of Mathematics and StatisticsPortland State UniversityPortland, OR 97201 E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

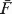Let X1, … , Xn be independent random variables with Xi having survival function λi, i = 1, … , n, and let Y1, … ,Yn be a random sample with common population survival distribution 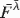, where 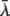= ∑i=1nλi/n. Let Xn:n and Yn:n denote the lifetimes of the parallel systems consisting of these components, respectively. It is shown that Xn:n is greater than Yn:n in terms of likelihood ratio order. It is also proved that the sample range Xn:n − X1:n is larger than Yn:n − Y1:n according to reverse hazard rate ordering. These two results strengthen and generalize the results in Dykstra, Kochar, and Rojo [6] and Kochar and Rojo [11], respectively.

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 21 , Issue 4 , October 2007 , pp. 597 - 609
Copyright
Copyright © Cambridge University Press 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Balakrishnan, N. & Rao, C.R. (1998). Handbook of statistics. Vol. 16: Order statistics: Theory and methods. New York: Elsevier.Google Scholar
2.Balakrishnan, N. & Rao, C.R. (1998). Handbook of statistics. Vol. 17: Order statistics: Applications. New York: Elsevier.Google Scholar
3.Boland, P.J., El-Neweihi, E. & Proschan, F. (1994). Applications of the hazard rate ordering in reliability and order statistics. Journal of Applied Probability 31: 180–192.CrossRefGoogle Scholar
4.Bon, J.L. & Paltanea, E. (1999). Ordering properties of convolutions of exponential random variables. Lifetime Data Analysis 5: 185–192.CrossRefGoogle ScholarPubMed
5.David, H.A. & Nagaraja, H.N. (2003). Order statistics, 3rd ed.New York: Wiley.CrossRefGoogle Scholar
6.Dykstra, R., Kochar, S.C. & Rojo, J. (1997). Stochastic comparisons of parallel systems of heterogeneous exponential components. Journal of Statistical Planning and Inference 65: 203–211.CrossRefGoogle Scholar
7.Khaledi, B. & Kochar, S.C. (2000). Some new results on stochastic comparisons of parallel systems. Journal of Applied Probability 37: 1123–1128.CrossRefGoogle Scholar
8.Khaledi, B. & Kochar, S.C. (2000). Sample range-some stochastic comparisons results. Calcutta Statistical Association Bulletin 50: 283–291.CrossRefGoogle Scholar
9.Khaledi, B. & Kochar, S.C. (2002). Dispersive ordering among linear combinatons of uniform random variables. Journal of Statistical Planning and Inference 100: 13–21.CrossRefGoogle Scholar
10.Khaledi, B. & Kochar, S.C. (2002). Stochastic orderings among order statistics and sample spacings. In Mara, J.C. (ed.), Uncertainty and optimality: Probability, statistics and operations research. Singapore: World Scientific, pp. 167–203.CrossRefGoogle Scholar
11.Kochar, S.C. & Rojo, J. (1996). Some new results on stochastic comparisons of spacings from heterogeneous exponential distributions. Journal of Multivariate Analysis 59: 272–281.CrossRefGoogle Scholar
12.Marshall, A.W. & Olkin, I. (1979). Inequalities: Theory of majorization and its applications. New York: Academic Press.Google Scholar
13.Mitrinović, D.S. (1970). Analytic inequalities. Berlin: Springer-Verlag.CrossRefGoogle Scholar
14.Müller, A. & Stoyan, D. (2002). Comparison methods for stochastic models and risks. New York: Wiley.Google Scholar
15.Pledger, P. & Proschan, F. (1971). Comparisons of order statistics and of spacings from heterogeneous distributions. In Rustagi, J.S. (ed.), Optimizing methods in statistics. New York: Academic Press, pp. 89–113.Google Scholar
16.Proschan, F. & Sethuraman, J. (1976). Stochastic comparisons of order statistics from heterogeneous populations, with applications in reliability. Journal of Multivariate Analysis 6: 608–616.CrossRefGoogle Scholar
17.Shaked, M. & Shanthikumar, J.G. (1994). Stochastic orders and their applications. San Diego: Academic Press.Google Scholar