Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-26T15:44:33.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Stochastic Comparison of Some Wear Processes

Published online by Cambridge University Press:  27 July 2009

Franco Pellerey  and
Moshe Shaked
Franco Pellerey
Affiliation:
Dipartimento di Matematica, Universitá di Milano, via L. Cicognara, 7, 20129 Milano, Italy
Moshe Shaked
Affiliation:
Department of Mathematics, University of Arizona, Tucson, Arizona 85721
Get access Rights & Permissions [Opens in a new window]

Abstract

Let [NA(t), t≥0] and [NB(t), t≥0] be two counting processes with independent interarrivals Ai and Bi, respectively, i ∈ 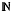+ ≡ [1,2,… ], and let [Xi, i ∈ 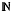+] and [Yi, i ∈ 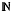+] be two sequences of independent non-negative random variables. Consider the two compound processes [U(t), t ≥ 0] and [V(t), t ≥ 0] defined as U(t) = 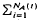Xi, t ≥ 0, and V(t) = 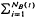Yi, t ≥ 0. Then it is well known (and not hard to verify) that if the Ai's are independent of the Xi's, and if the Bi's are independent of the yi's, and if Ai ≥st Bi and Xi ≤st Yi, for all i ∈ 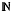+, then [U(t), t ≥ 0] ≤st [V(t), t ≥ 0]. In this paper we provide conditions under which this stochastic order relation holds even if Ai ≤st Bi and/or Xi ≥st Yi for all i ∈ 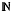+. In fact, we derive the stochastic order relationships among processes that are much more general than the cumulative ones described above. For example, it is not necessarily assumed that the Ai's are independent of the Xi's or that the Bi's are independent of the Yi's. Examples that illustrate the applications of the theory are included.

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 7 , Issue 3 , July 1993 , pp. 421 - 435
Copyright
Copyright © Cambridge University Press 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Ammann, L.P. (1984). Bayesian nonparametric inference for quantal response data. Annals of Statistics 12: 636–645.CrossRefGoogle Scholar
2.Arnold, B.C. & Villaseñor, J.A. (1986). Lorenz ordering of means and medians. Statistics and Probability Letters 4: 47–49.CrossRefGoogle Scholar
3.Block, H.W. & Savits, T.H. (1978). Shock models with NBUE survival. Journal of Applied Probability 15: 621–628.CrossRefGoogle Scholar
4.Daley, D.J. & Rolski, T. (1984). Some comparability results for waiting times in single- and many-server queues. Journal of Applied Probability 21: 887–900.CrossRefGoogle Scholar
5.Gaver, D.P. & Miller, R.G. (1962). Limiting distributions for some storage problems. In Arrow, K.J., Karlin, S., & Scarf, H. (eds.), Studies in applied probability and management science. Stanford, CA: Stanford University Press, pp. 110–126.Google Scholar
6.Kebir, Y. (1991). On hazard rate processes. Naval Research Logistics 38: 865–876.CrossRefGoogle Scholar
7.Marshall, A.W. & Shaked, M. (1983). New better than used processes. Advances in Applied Probability 15: 601–615.CrossRefGoogle Scholar
8.Miller, D.R. (1979). Almost sure comparisons of renewal processes and Poisson processes, with applications in reliability theory. Mathematics of Operations Research 4: 406–413.CrossRefGoogle Scholar
9.Padgett, W.J. & Wei, L.J. (1981). A Bayesian nonparametric estimator of survival probability assuming increasing failure rate. Communications in Statistics — Theory and Methods A10: 49–63.CrossRefGoogle Scholar
10.Pellerey, F. (1993). Caratterizzazioni di Affidabilità ed Ordinamenti Parziali per Modelli di Shock. Ph.D. dissertation, Dipartimento di Matematica, Università di Milano.Google Scholar
11.Pellerey, F. & Shaked, M. (1992). Stochastic comparison of some wear processes. Technical Report, Department of Mathematics, University of Arizona, Tucson.Google Scholar
12.Reynolds, D.S. & Savage, I.R. (1971). Random wear models in reliability theory. Advances in Applied Probability 3: 229–248.CrossRefGoogle Scholar
13.Ross, S.M. (1983). Stochastic processes. New York: Wiley.Google Scholar
14.Shaked, M. & Shanthikumar, J.G. (1988). On the First failure time of dependent multicomponent reliability systems. Mathematics of Operations Research 13: 50–64.CrossRefGoogle Scholar
15.Shanthikumar, J.G. (1984). Processes with new better than used first passage times. Advances in Applied Probability 16: 667–686.CrossRefGoogle Scholar
16.Sonderman, D. (1980). Comparing semi-Markov processes. Mathematics of Operations Research 5: 110–119.CrossRefGoogle Scholar
17.Stoyan, D. (1983). Comparison methods for queues and other stochastic models. New York: Wiley.Google Scholar
18.Whitt, W. (1981). Comparing counting processes and queues. Advances in Applied Probability 13: 207–220.CrossRefGoogle Scholar