Published online by Cambridge University Press: 26 July 2021
Let  $\{Y_{1},\ldots ,Y_{n}\}$ be a collection of interdependent nonnegative random variables, with
$\{Y_{1},\ldots ,Y_{n}\}$ be a collection of interdependent nonnegative random variables, with 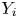 $Y_{i}$ having an exponentiated location-scale model with location parameter
$Y_{i}$ having an exponentiated location-scale model with location parameter 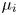 $\mu _i$, scale parameter
$\mu _i$, scale parameter 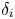 $\delta _i$ and shape (skewness) parameter
$\delta _i$ and shape (skewness) parameter 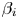 $\beta _i$, for
$\beta _i$, for 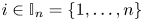 $i\in \mathbb {I}_{n}=\{1,\ldots ,n\}$. Furthermore, let
$i\in \mathbb {I}_{n}=\{1,\ldots ,n\}$. Furthermore, let  $\{L_1^{*},\ldots ,L_n^{*}\}$ be a set of independent Bernoulli random variables, independently of
$\{L_1^{*},\ldots ,L_n^{*}\}$ be a set of independent Bernoulli random variables, independently of 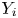 $Y_{i}$'s, with
$Y_{i}$'s, with 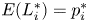 $E(L_{i}^{*})=p_{i}^{*}$, for
$E(L_{i}^{*})=p_{i}^{*}$, for 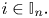 $i\in \mathbb {I}_{n}.$ Under this setup, the portfolio of risks is the collection
$i\in \mathbb {I}_{n}.$ Under this setup, the portfolio of risks is the collection  $\{T_{1}^{*}=L_{1}^{*}Y_{1},\ldots ,T_{n}^{*}=L_{n}^{*}Y_{n}\}$, wherein
$\{T_{1}^{*}=L_{1}^{*}Y_{1},\ldots ,T_{n}^{*}=L_{n}^{*}Y_{n}\}$, wherein 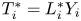 $T_{i}^{*}=L_{i}^{*}Y_{i}$ represents the
$T_{i}^{*}=L_{i}^{*}Y_{i}$ represents the 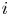 $i$th claim amount. This article then presents several sufficient conditions, under which the smallest claim amounts are compared in terms of the usual stochastic and hazard rate orders. The comparison results are obtained when the dependence structure among the claim severities are modeled by (i) an Archimedean survival copula and (ii) a general survival copula. Several examples are also presented to illustrate the established results.
$i$th claim amount. This article then presents several sufficient conditions, under which the smallest claim amounts are compared in terms of the usual stochastic and hazard rate orders. The comparison results are obtained when the dependence structure among the claim severities are modeled by (i) an Archimedean survival copula and (ii) a general survival copula. Several examples are also presented to illustrate the established results.