Hostname: page-component-669899f699-7xsfk Total loading time: 0 Render date: 2025-04-25T19:19:55.601Z Has data issue: false hasContentIssue false
  • English
  • Français

On the distribution of winners’ scores in a round-robin tournament

Part of: Nonparametric inference Graph theory

Published online by Cambridge University Press:  06 August 2021

Yaakov Malinovsky Open the ORCID record for Yaakov Malinovsky [Opens in a new window]
Yaakov Malinovsky*
Affiliation:
Department of Mathematics and Statistics, University of Maryland, Baltimore County, Baltimore, MD 21250, USA. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In a classical chess round-robin tournament, each of 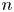$n$ players wins, draws, or loses a game against each of the other $n-1$ players. A win rewards a player with 1 points, a draw with 1/2 point, and a loss with 0 points. We are interested in the distribution of the scores associated with ranks of 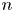$n$ players after 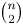${{n \choose 2}}$ games, that is, the distribution of the maximal score, second maximum, and so on. The exact distribution for a general 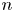$n$ seems impossible to obtain; we obtain a limit distribution.

Keywords

ExtremesNegative correlation

MSC classification

Primary: 62G32: Statistics of extreme values; tail inference
Secondary: 05C20: Directed graphs (digraphs), tournaments
Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 36 , Issue 4 , October 2022 , pp. 1098 - 1102
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Berman, S.M. (1964). Limiting distribution of the maximum of a diffusion process. Annals of Mathematical Statistics 35: 319–329.CrossRefGoogle Scholar
Courant, R. & Robbins, H. (1996). What is mathematics? An elementary approach to ideas and methods, 2nd ed., revised by Ian Stewart. New York: Oxford University Press.Google Scholar
Cramér, H. (1946). Mathematical methods of statistics. Princeton: Princeton University Press.Google Scholar
Galambos, J. (1987). The asymptotic theory of extreme order statistics. 2nd ed. Malabar, FL: Krieger.Google Scholar
Grimmett, G.R. & Stirzaker, D.R. (2020). Probability and random processes, 4th ed. Oxford: Oxford University Press.Google Scholar
Gumbel, E.J. (1958). Statistics of extemes. New York: Columbia University Press.CrossRefGoogle Scholar
Huber, P.J. (1963). A remark on a paper of Trawinski and David entitled: Selection of the best treatment in a paired comparison experiment. Annals of Mathematical Statistics 34: 92–94.CrossRefGoogle Scholar
Leadbetter, M.R. (2017). Extremes under dependence–historical development and parallels with central limit theory. In Extreme events in finance, Wiley Handb. Finance Eng. Econom. Edited by Francois Longin. Hoboken: Wiley, pp. 11–23.Google Scholar
Leadbetter, M.R., Lindgren, G., & Rootzén, H. (1983). Extremes and related properties of random sequences and processes. Springer Series in Statistics. New York-Berlin: Springer-Verlag.CrossRefGoogle Scholar
Lehmann, E.L. (1998). Elements of large-sample theory. New York: Springer.Google Scholar
Malinovsky, Y. & Moon, J.W. (2021). On the negative dependence inequalities and maximal score in round-robin tournament. https://arxiv.org/abs/2104.01450.Google Scholar
Moon, J.W. (2013). Topics on tournaments. [Publicaly available on website of Project Gutenberg https://www.gutenberg.org/ebooks/42833].Google Scholar
Ross, S.M. (2021). Team's seasonal win probabilities. Probability in the Engineering and Informational Sciences. doi:10.1017/S026996482100019X. In press.CrossRefGoogle Scholar