Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-17T00:17:16.026Z Has data issue: false hasContentIssue false
  • English
  • Français

Convergence of Departures in Tandem Networks of·/GI/ ∞ Queues

Published online by Cambridge University Press:  27 July 2009

B. Prabhakar ,
T. S. Mountford  and
N. Bambos
B. Prabhakar
Affiliation:
Department of Mathematics, University of California at Los Angeles Los Angeles, California 90024
T. S. Mountford
Affiliation:
Department of Mathematics, University of California at Los Angeles Los Angeles, California 90024
N. Bambos
Affiliation:
Department of Mathematics, University of California at Los Angeles Los Angeles, California 90024
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider an infinite series of independent and identical -/GI/∞ queues fed by an arbitrary stationary and ergodic arrival process, A1. Let Ai be the arrival process to the ith node, and let νi be the law of Ai. Denote by 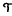(·) the input–output map of the ·/GI/∞ node; that is, νi+1 = 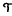(νi). It is known that the Poisson process is a fixed point for 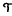. In this paper, we are interested in the asymptotic distribution of the departure process from the nth node, νn+1 = 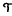n(ν1), as n ∞. Using couplings for random walks, this limiting distribution is shown to be either a Poisson process or a stationary ν-Poisson process, depending on the joint distribution of A1 and the service process. This generalizes a result of Vere-Jones (1968, Journal of the Royal Statistical Society, Series B 30: 321–333) and is similar in flavor to Mountford and Prabhakar (1995, Annals of Applied Probability 5(1): 121–127), where Poisson convergence is established for departures from a series of exponential server queues using coupling methods.

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 10 , Issue 4 , October 1996 , pp. 487 - 500
Copyright
Copyright © Cambridge University Press 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Anantharam, V. (1993). Uniqueness of stationary ergodic fixed point for a /M/k node. Annals of Applied Probability 3(1): 154–173.CrossRefGoogle Scholar
2.Bambos, N. & Prabhakar, B. (1994). On infinite queueing tandems. Systems & Control Letters 23: 305–314.CrossRefGoogle Scholar
3.Bambos, N. & Walrand, J. (1990). An invariant distribution for the G/G/l queueing operator. Advances in Applied Probability 22: 254–256.CrossRefGoogle Scholar
4.Daley, D. J. & Vere-Jones, D. (1988). An introduction to the theory of point processes. Springer Series in Statistics. New York: Springer.Google Scholar
5.Durrett, R. (1991). Probability: Theory and examples. Belmont, CA: Wadsworth.Google Scholar
6.Glynn, P.W. & Whitt, W. (1991). Departures from many queues in series. Annals of Applied Probability 1(4): 546–572.CrossRefGoogle Scholar
7.Kelly, F.P. (1979). Reversibility and stochastic networks. Wiley Series in Probability and Mathematical Statistics. New York: Wiley.Google Scholar
8.Kleinrock, L. (1964). Communication nets: Stochastic message flow and delay. New York: Dover.Google Scholar
9.Lindvall, T. (1992). Lectures on the coupling method. Wiley Series in Probability and Mathematical Statistics. New York: Wiley.Google Scholar
10.Mountford, T.S. & Prabhakar, B. (1995). On the weak convergence of departures from an infinite sequence of /M/l queues. Annals of Applied Probability 5(1): 121–127.CrossRefGoogle Scholar
11.Vere-Jones, D. (1968). Some applications of probability generating functionals to the study of input-output streams. Journal of the Royal Statistical Society Series B 30: 321–333.Google Scholar