Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-10T07:05:39.710Z Has data issue: false hasContentIssue false
  • English
  • Français

CHARACTERIZATIONS OF OPTIMAL POLICIES IN A GENERAL STOPPING PROBLEM AND STABILITY ESTIMATING

Published online by Cambridge University Press:  05 June 2014

Evgueni Gordienko  and
Andrey Novikov
Evgueni Gordienko
Affiliation:
Department of Mathematics, UAM-Iztapalapa, San Rafael Atlixco 186, col. Vicentina, C.P. 11320, Mexico City, Mexico E-mail: [email protected] and [email protected]
Andrey Novikov
Affiliation:
Department of Mathematics, UAM-Iztapalapa, San Rafael Atlixco 186, col. Vicentina, C.P. 11320, Mexico City, Mexico E-mail: [email protected] and [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider an optimal stopping problem for a general discrete-time process X1, X2, …, Xn, … on a common measurable space. Stopping at time n (n = 1, 2, …) yields a reward Rn(X1, …, Xn) ≥ 0, while if we do not stop, we pay cn(X1, …, Xn) ≥ 0 and keep observing the process. The problem is to characterize all the optimal stopping times τ, i.e., such that maximize the mean net gain:

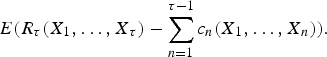$$E(R_\tau(X_1,\dots,X_\tau)-\sum_{n=1}^{\tau-1}c_n(X_1,\dots,X_n)).$$
We propose a new simple approach to stopping problems which allows to obtain not only sufficient, but also necessary conditions of optimality in some natural classes of (randomized) stopping rules.

In the particular case of Markov sequence X1, X2, … we estimate the stability of the optimal stopping problem under perturbations of transition probabilities.

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 28 , Issue 3 , July 2014 , pp. 335 - 352
Copyright
Copyright © Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Allart, P. (2004). Optimal stopping rules for correlated random walks with a discount. Journal of Applied Probability 41: 483–496.CrossRefGoogle Scholar
2.Allart, P. & Montecino, M. (2008). Optimal buy/sell rules for correlated random walks. Journal of Applied Probability 45: 33–44.Google Scholar
3.Arrow, K.J., Blackwell, D. & Girshik, M.A. (1949). Bayes and minimax solutions of sequential decision problems. Econometrica 17 (3/4): 213–244.Google Scholar
4.Bacchus, F., Boutilier, C. & Grove, A. (1997). Structured Solution Methods for non-markovian decision processes. Proc. 14th National Conf. AI (AAAI-97), Providence, August.Google Scholar
5.Baird, H.S. & Mallows, C.L. (1997). The evolution of a problem. Statistica Sinica 7: 211–220.Google Scholar
6.Chow, Y.S., Robbins, H. & Siegmund, D. (1971). Great Expectations: The Theory of Optimal Stopping. Boston: Houghton Mifflin Company.Google Scholar
7.Devroye, L. (1985). Nonparametric Density Estimation. The L1 View. New York: Wiley.Google Scholar
8.Dufour, F. & Piunovski, A.B. (2010). Multiobjective stopping problem for discrete-time Markov processes: convex analytic approach. Journal of Applied Probability 47: 947–966.Google Scholar
9.Ferguson, T.S. (1967). Mathematical Statistics: A Decision Theoretic Approach. New York: Academic Press.Google Scholar
10.Ghosh, M., Mukhopadhyay, N. & Sen, P.K. (1997). Sequential Estimation. New York: Wiley.Google Scholar
11.Gikhman, I.I. & Skorokhod, A.V. (1977). Controllable Stochastic Processes (in Russian). Kiev: Naukova dumka.Google Scholar
12.Gordienko, E.I. (1992). An estimate of the stability of optimal control of certain stochastic and deterministic systems. Journal of Soviet Mathematics 59: 891–899 (Translated from Russian publication of 1989).CrossRefGoogle Scholar
13.Gordienko, E.I. & Yushkevich, A.A. (2003). Stability estimates in the problem of average optimal switching of a Markov chain. Mathematical Methods of Operations Research 57: 345–365.Google Scholar
14.Han, D. & Tsung, F. (2009). The optimal stopping time for detecting changes in discrete Markov processes. Sequential Analysis 28: 115–135.Google Scholar
15.Hinderer, K. (1970). Foundations of non-stationary dynamic programming with discrete time parameter. Lecture Notes in Operations Research and Mathematical Systems, 33, Berlin: Springer.Google Scholar
16.Hordijk, A. (1974). Dynamic Programming and Markov Potential Theory, 2nd ed. Mathematical Centre Tracts 51, Amsterdam: Mathematisch Centrum.Google Scholar
17.Horiguchi, M. (2001). Markov decision processes with a stopping time constraint. Mathematical Methods of Operations Research 53: 279–295.Google Scholar
18.Jensen, V. (1997). An optimal stopping problem in risk theory. Scand Actuarial J. 2:149–159.CrossRefGoogle Scholar
19.Kalashnikov, V.V. (1994). Mathematical Methods in Quening Theory. Dordrecht: Kluwer Academic.CrossRefGoogle Scholar
20.Kühne, R. & Rüschendorf, L. (2004). Approximate optimal stopping of dependent sequences. Theory of Probability and its Application, 48: 465–480.Google Scholar
21.Meyn, S.P. & Tweedie, R.L. (1993). Markov Chains and Stochastic Stability. London: Springer-Verlag.Google Scholar
22.Matskyavichyus, V. (1973). Passing to the limit in optimal stopping problem for Markov processes. Translated from Litovskii Matematicheskii Sbornik, 13(1): 115–128.Google Scholar
23.Morali, N. & Soyer, R. (2002). Optimal stopping in software testing. Naval Research Logistics, 50(1): 88–104.CrossRefGoogle Scholar
24.Muciek, B.K. (2002). Optimal stopping of a risk process model with interest rates. Journal of Applied Probability 39: 261–270.CrossRefGoogle Scholar
25.Novikov, A. (2009). Optimal sequential multiple hypothesis testing in presence of control variables. Kybernetika 45(3): 507–528.Google Scholar
26.Novikov, A. (2009). Optimal sequential multiple hypothesis tests. Kybernetika 45(2): 309–330.Google Scholar
27.Novikov, A. (2009). Optimal sequential tests for two simple hypotheses. Sequential Analysis 28(2): 188–217.CrossRefGoogle Scholar
28.Novikov, A. (2010). Optimal sequential procedures with Bayes decision rules. Kybernetika 46(4): 754–770.Google Scholar
29.Novikov, A. & Novikov, P. (2010). Locally most powerful sequential tests of a simple hypothesis vs. one-sided alternatives. Journal of Statistical Planning and Inference 140(3): 750–765.CrossRefGoogle Scholar
30.Rieder, U. (1975). On stopped decision processes with discrete time parameter. Stochastic Processes and their Applications 3: 365–383.Google Scholar
31.Ross, Sh.M. (1970). Applied probability models with optimization applications, New York: Dover Publications, Inc. plans and sequential probability ratio tests. Journal of the American Statistical Association 65(329): 431–437.Google Scholar
32.Shiryaev, A.N. (1978). Optimal Stopping Rules. New York: Springer-Verlag.Google Scholar
33.Shiryaev, A.N. (1999). Essential of Stocastic Finance: Facts, Models, Theory. River Edge, NJ: World Scientific.CrossRefGoogle Scholar
34.Thiebaux, S., Gretton, Ch., Slaney, J. & Price, D. (2006). Decision-theoretic planning with non-Markovian rewards. Journal of Artificial Intelligence Research 25: 17–74.Google Scholar
35.Wald, A. (1947). Sequential Analysis. New York: Wiley.Google Scholar
36.Wald, A. & Wolfowitz, J. (1948). Optimum character of the sequential probability ratio test. Annals of Mathematical Statistics 19: 326–339.Google Scholar
37.Zaitseva, E. (2008). Stability estimating in optimal stopping problem. Kybernetika 44: 400–415.Google Scholar