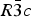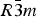I. INTRODUCTION
Calcite is a polymorph of calcium carbonate (CaCO3). The room-temperature structure of calcite (Phase I) was first determined by Bragg (Reference Bragg1914). Preceding Bragg's groundbreaking study, a phase transition of calcite at approximately 1243 ± 5 K had been reported by Boeke (Reference Boeke1912). This high-temperature phase, which was named as Phase V by Mirwald (Reference Mirwald1976), has been a key controversial issue in the field of common minerals for over a hundred years (Tsuboi, Reference Tsuboi1927; Mirwald, Reference Mirwald1979; Markgraf and Reeder, Reference Markgraf and Reeder1985; Dove and Powell, Reference Dove and Powell1989; Hagen et al., Reference Hagen, Dove, Harris, Steigenberger and Powell1992; Maslen et al., Reference Maslen, Streltsov and Streltsova1993; Dove et al., Reference Dove, Swainson, Powell and Tennant2005; Antao et al., Reference Antao, Hassan, Mulder, Lee and Toby2009). The structure of Phase V was finally determined in our previous study (Ishizawa et al., Reference Ishizawa, Setoguchi and Yanagisawa2013), and is briefly reviewed here, in addition to the intermediate Phase IV that bridges Phases I and V.
II. EXPERIMENTAL METHODS
Transparent and colorless single crystals of calcite were grown by the hydrothermal method at the Research Laboratory of Hydrothermal Chemistry, Faculty of Science, Kochi University. Single-crystal X-ray diffraction experiments (Mo Kα) were carried out using a three-circle diffractometer with a charge-coupled device area detector (Bruker Apex II). An appropriate choice in sample mounting methodology was necessary to observe the phase transitions of calcite at elevated temperatures, as thermal decomposition often precedes the phase transitions, depending on the experimental conditions. In this study, three methods were examined, as shown in Figure 1: (1) the sample (hs11) was mounted on top of a silica glass capillary with cement; (2) the sample (hs23) was sealed in a silica glass capillary in an air atmosphere; and (3) the sample (hs25) was sealed in a silica glass capillary in a carbon dioxide gas atmosphere. The experimental details are given in the original paper (Ishizawa et al., Reference Ishizawa, Setoguchi and Yanagisawa2013). Structural analysis and volumetric plotting were done using the programs Jana2006 (Petricek et al., Reference Petricek, Dusek and Palatinus2006) and Vesta (Momma and Izumi, Reference Momma and Izumi2011), respectively.

Figure 1. (Color online) Thermal decomposition of calcite samples recorded on X-ray rotation photographs. Sample hs11 (top row), exposed to a hot air stream, decomposed after the data collection at 839 K. Sample hs23, sealed in a capillary in an air atmosphere (middle row), almost decomposed after the data collection at 1192 K. Sample hs25, sealed in a carbon dioxide atmosphere (bottom row), did not decompose during the data collection at 1275 K. A schematic powder pattern of calcium oxide (CaO) is superimposed on the beam stop shadow in each rotation X-ray photograph.
III. RESULTS AND DISCUSSION
The three methods of sample preparation gave different results regarding the decomposition temperature of calcite. The sample hs11 (top row in Figure 1), which was exposed directly to a hot air stream, decomposed at approximately 839 K, at which diffraction spots of calcite disappeared on the rotation photograph taken after data collection. The crystalline reaction product, calcium oxide (CaO), was identified from powder diffraction rings recorded in the rotation photograph, suggesting complete decomposition of the CaCO3 crystal into CaO during the heat treatment at 839 K.
Sample hs23 (middle row in Figure 1), which was sealed in a capillary in an air atmosphere at room temperature, survived at temperatures much higher than 839 K. The sample finally decomposed during the data collection at 1192 K, which enabled observation of a reversible I–IV phase transition at approximately 985 K. The rotation photograph taken after the experiment at 1192 K (rightmost panel in the middle row) showed two extra powder rings other than those of CaO. These extra rings were found only in hs23, and appeared to be fine particles of calcium silicate deposited on the inner wall of the silica glass capillary.
The sample hs25, sealed in a carbon dioxide atmosphere (bottom row in Figure 1), did not decompose during the data collection at 1275 K. A reversible IV–V transition at approximately 1240 K was thus observed. Phase V was stable over a narrow temperature range between 1240 and 1275 K in this experiment. The pressure of the carbon dioxide atmosphere was estimated to be approximately 0.4 MPa at 1300 K, assuming a constant volume for the sealed silica capillary. The sample hs25 immediately decomposed when the temperature was raised above 1275 K. The solid reaction product (CaO) retained the original shape of the parent calcite, although numerous nanopores were found in the scanning electron micrograph (Figure S2c in the Supplementary information, Ishizawa et al., Reference Ishizawa, Setoguchi and Yanagisawa2013).
The structures of Phases I and IV belong to the same space group ![]() $R\bar 3c$, with almost identical unit cell dimensions. The I–IV transition can thus be described as an orientational order/disorder transition of the carbonate group, occurring within the same space group
$R\bar 3c$, with almost identical unit cell dimensions. The I–IV transition can thus be described as an orientational order/disorder transition of the carbonate group, occurring within the same space group ![]() $R\bar 3c$. The probability density function is useful in describing the behavior of atoms vibrating anharmonically (Willis and Pryor, Reference Willis and Pryor1975). The joint-probability density function of the oxygen atoms of the carbonate group is shown in Figure 2, which is imported from Figure 4 in the original paper. The anharmonic atomic displacement parameters (ADPs) up to the third-order expansion of the Gram–Charlier series were used for this calculation. As the oxygen atoms in Phase I are gently and almost harmonically vibrating at the original site determined by Bragg (Reference Bragg1914), structure refinements assuming isotropic or anisotropic ADP are applicable and successful. However, such harmonic approximation becomes difficult to apply in Phase IV, as the probability-density function of the oxygen atoms expands directionally during heating, causing their 90% isosurfaces to become connected to each other. This difficulty was overcome by employing a split-atom model for the oxygen atoms with harmonic vibration. The oxygen population of the split atom site (O2 in Figure 2) increases with the temperature exponentially from 0 to 50% in the range between 985 and 1240 K, where Phase IV is stable [see Figure 3(d) of the original paper].
$R\bar 3c$. The probability density function is useful in describing the behavior of atoms vibrating anharmonically (Willis and Pryor, Reference Willis and Pryor1975). The joint-probability density function of the oxygen atoms of the carbonate group is shown in Figure 2, which is imported from Figure 4 in the original paper. The anharmonic atomic displacement parameters (ADPs) up to the third-order expansion of the Gram–Charlier series were used for this calculation. As the oxygen atoms in Phase I are gently and almost harmonically vibrating at the original site determined by Bragg (Reference Bragg1914), structure refinements assuming isotropic or anisotropic ADP are applicable and successful. However, such harmonic approximation becomes difficult to apply in Phase IV, as the probability-density function of the oxygen atoms expands directionally during heating, causing their 90% isosurfaces to become connected to each other. This difficulty was overcome by employing a split-atom model for the oxygen atoms with harmonic vibration. The oxygen population of the split atom site (O2 in Figure 2) increases with the temperature exponentially from 0 to 50% in the range between 985 and 1240 K, where Phase IV is stable [see Figure 3(d) of the original paper].

Figure 2. (Color online) Isosurface plots of the joint-probability density function of the oxygen atoms in the carbonate group at selected temperatures, as in Figure 4 of the original paper (Ishizawa et al., Reference Ishizawa, Setoguchi and Yanagisawa2013). The isosurface levels are the top 10, 50, and 90% probabilities from the interior.

Figure 3. (Color online) Schematic drawings of the carbonate group in Phase V; the undulated circular orbital is represented with 90 oxygen atoms surrounding the carbon atom (left), and four representative states during the assumed rotation of the oxygen triangle along the orbital are shown (right). The oxygen triangle repeats the umbrella inversion by way of these states, i.e., (1) the ground state (no distortion), (2) the excited state 1 with the umbrella distortion, (3) the ground state (no distortion), and (4) the exited state 2 with the inverse umbrella distortion (counterclockwise from the leftmost state in the right panel).

Figure 4. TLS-uncorrected (open marks) and corrected (filled marks) intramolecular C–O bond distance as a function of temperature, according to the Supplementary Information of Ishizawa et al. (Reference Ishizawa, Setoguchi and Yanagisawa2013).
Phase IV turns into V at approximately 1240 K. The space group changes from ![]() $R\bar 3c$ to
$R\bar 3c$ to ![]() $R\bar 3m$, with the c-length being halved. In Phase V, the oxygen atoms exist with equal probability along the undulated circular orbital around the central carbon (rightmost panel in the bottom row of Figure 2). This scenario could not be modeled using the harmonic approximation, as the oxygen sublattice is melted. Considering the resonance structure of the carbonate group, the three oxygen atoms of the carbonate group should exist with nearly 120° separation along the circular orbital. Since the circular orbital is undulated, it appears that the three oxygen atoms still form a triangle and move about the central carbon along the undulated orbital, as shown in Figure 3. The amplitude of the undulation and the magnitude of the ADPs of the carbon and oxygen atoms suggest that the carbonate group in Phase V is no longer flat on the basal plane when the oxygen triangle comes to troughs or peaks in the undulated orbital, but is instead deformed like an umbrella. The undulation appears to be caused by the repulsion between electron clouds of the oxygen and calcium atoms.
$R\bar 3m$, with the c-length being halved. In Phase V, the oxygen atoms exist with equal probability along the undulated circular orbital around the central carbon (rightmost panel in the bottom row of Figure 2). This scenario could not be modeled using the harmonic approximation, as the oxygen sublattice is melted. Considering the resonance structure of the carbonate group, the three oxygen atoms of the carbonate group should exist with nearly 120° separation along the circular orbital. Since the circular orbital is undulated, it appears that the three oxygen atoms still form a triangle and move about the central carbon along the undulated orbital, as shown in Figure 3. The amplitude of the undulation and the magnitude of the ADPs of the carbon and oxygen atoms suggest that the carbonate group in Phase V is no longer flat on the basal plane when the oxygen triangle comes to troughs or peaks in the undulated orbital, but is instead deformed like an umbrella. The undulation appears to be caused by the repulsion between electron clouds of the oxygen and calcium atoms.
The intramolecular C–O bond length in calcite as a function of temperature is shown in Figure 4. As Markgraf and Reeder (Reference Markgraf and Reeder1985) first pointed out, an apparent decrease in the intramolecular C–O bond length in calcite occurs with increasing temperature in the conventional refinement. This is an artifact caused by the assumption that the constituent atoms are vibrating independently in a crystal. This problem can be partly overcome by introducing the Translation–Libration–Screw (TLS) analysis (Willis and Pryor, Reference Willis and Pryor1975) for the CO3 molecular moiety in the least-squares procedure, as shown in Figure 4. The TLS modeling is also useful in the Rietveld powder refinement because it can generally reduce the number of refinable parameters to model the vibration of a molecular moiety. However, it should be noted that the TLS refinement is applicable only to the case where atomic vibrations are not very large. For example, Phase V does not conform to such TLS modeling, given that the oxygen sublattice is melted.
The thermal decomposition of calcite was conventionally believed to proceed according to the following reaction (Searcy and Beruto, Reference Searcy and Beruto1976, Reference Searcy and Beruto1978; Matvienko et al., Reference Matvienko, Chizhik and Sidel'nikov2013):
Bayarjargal et al. (Reference Bayarjargal, Shumilova, Friedrich and Winkler2010), however, proposed an alternative decomposition reaction on the basis of their experimental observation of diamond formation from calcite under high pressure and temperature,
This reaction consists of the following elementary reactions:
It is noted that if Eq. (2) actually occurs in the present study, the carbon atoms that emerge on the surface of the crystal will immediately react with a carbon dioxide molecule through the Boudouard reaction (Holleman et al., Reference Holleman, Wiber and Wiberg2001),
The product of Eq. (7), carbon monoxide, is then oxidized by the dioxygen reaction product of Eq. (5), emerging from the interior to the crystal surface through the nanopores,
As the rate of the Boudouard reaction, Eq. (7), increases with temperature to approximately 100% at 1273 K, it is difficult to detect the presence of carbon on the crystal surface in the present case.
Although identification of the true reaction mechanism of the thermal decomposition of calcite remains unresolved in the present study, the mechanism based on Eq. (2) appears to have several advantages, namely: (1) The gaseous dioxygen molecule [Eqs (2) and (5)] has a smaller radius, a longer mean free path, and a faster velocity than the carbon dioxide molecule (Tables of Physical & Chemical Constants, 2005), which enables easier outer diffusion of dioxygen gas through the nanometer-sized open pores observed in the decomposed crystal; and (2) the elemental carbon atom [Eqs (2) and (4)] can diffuse rapidly through the crystal lattices of the calcite parent crystal and/or the CaO reaction product crystal.
IV. CONCLUSION
Our recent study on the structural evolution of calcite at elevated temperatures (Ishizawa et al., Reference Ishizawa, Setoguchi and Yanagisawa2013) appears to have solved an enduring mystery of over a hundred years, dating from the finding of a reversible phase transition of calcite by Boeke in Reference Boeke1912, and following W. L. Bragg's structure determination at room temperature in 1914. Crystals of calcite sealed in a silica glass capillary in a carbon dioxide atmosphere undergo reversible phase transitions between Phases I, IV, and V in this order with increasing temperature. The I–IV and IV–V transition points are at approximately 985 and 1240 K, respectively. Phase V is stable only over a narrow temperature range between 1240 and 1275 K, above which the crystals immediately decompose.
The I–IV transition can be described as an orientational order/disorder transition of the carbonate group, occurring within the same space group ![]() $R\bar 3c$. In Phase V, the oxygen sublattice is melted. The joint-probability density function, calculated from the inverse Fourier transform of the anharmonic ADPs, reveals that the oxygen triangles of the carbonate group in Phase V do not sit still at specified Wyckoff positions in the space group
$R\bar 3c$. In Phase V, the oxygen sublattice is melted. The joint-probability density function, calculated from the inverse Fourier transform of the anharmonic ADPs, reveals that the oxygen triangles of the carbonate group in Phase V do not sit still at specified Wyckoff positions in the space group ![]() $R\bar 3m$, but are instead distributed with equal probability along the undulated circular orbital about the central carbon. The carbonate group in Phase V appears to no longer be flat on the basal plane when the oxygen triangle comes to troughs or peaks in the undulated orbital, but is instead deformed like an umbrella. If the oxygen triangle migrates about carbon, the carbonate group should then repeat the umbrella inversion in Phase V as a function of time.
$R\bar 3m$, but are instead distributed with equal probability along the undulated circular orbital about the central carbon. The carbonate group in Phase V appears to no longer be flat on the basal plane when the oxygen triangle comes to troughs or peaks in the undulated orbital, but is instead deformed like an umbrella. If the oxygen triangle migrates about carbon, the carbonate group should then repeat the umbrella inversion in Phase V as a function of time.
The decomposition mechanism, CaCO3 → CaO + C + O2, recently proposed by Bayarjargal et al. (Reference Bayarjargal, Shumilova, Friedrich and Winkler2010) is advantageous in terms of releasing the gaseous product from the interior to the exterior through numerous nanopores formed in the solid reaction product, as compared with the conventional reaction mechanism, CaCO3 → CaO + CO2. The former mechanism also allows for improvement in the various calcination processes used in many manufacturing industries, helping to reduce the emission of carbon dioxide in the Earth's atmosphere.
ACKNOWLEDGEMENTS
The original paper reviewed here was co-authored by Hayato Setoguchi, Nagoya Institute of Technology, and Professor Kazumichi Yanagisawa, Research Laboratory of Hydrothermal Chemistry, Kochi University. We thank Dr. Vaclav Petricek at the Institute of Physics, Academy of Science, Czech Republic, for his implementation of the Jana2006 program package, Tomomi Gotoda at Research Laboratory of Hydrothermal Chemistry, Kochi University, for her help with the growth of calcite crystals, Hisashi Hibino at Nagoya Institute of Technology, for his help with the EDS and SEM analyses, Associate Professor Jung Wang from the Inner Mongolia University of Technology, and Dr. Terutoshi Sakakura from the Institute of Multidisciplinary Research for Advanced Materials, Tohoku University, Japan, for their help in the preliminary stage of this work. This work was supported by JSPS KAKENHI Grant number 22360272.