Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-05T14:42:14.942Z Has data issue: false hasContentIssue false
  • English
  • Français

Powder Diffraction Data for Two Energetic Materials and a Proposed Intensity Figure of Merit

Published online by Cambridge University Press:  10 January 2013

Charlotte K. Lowe-Ma
Charlotte K. Lowe-Ma
Affiliation:
Chemistry Division, Research Department Naval Weapons Center, China Lake, California 93555, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

Indexed X-ray powder diffraction data are reported for two energetic materials, oxalylhydroxamic acid and 2-diazo-4, 6-dinitrophenol (DDNP). For these two compounds, powder diffraction data calculated from single-crystal structure determinations are also presented and compared to the experimentally observed powder diffraction data. To evaluate the reliability of the experimentally obtained intensities, an intensity figure of merit, IX(N), based on an average percent difference between observed and calculated intensities for a limited number of strong and moderately-strong lines is proposed as a more useful measure of agreement than R1. For N lines with Icalc > X% relative intensity, IX(N) is defined as

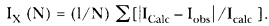
This is compared to

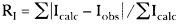
which involves a summation over all lines.

Type
Research Article
Information
Powder Diffraction , Volume 6 , Issue 1 , March 1991 , pp. 31 - 35
Copyright
Copyright © Cambridge University Press 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Blanchard, F.N. (1989a). Pow. Diff. 4(3), 172–173.CrossRefGoogle Scholar
Blanchard, F.N. (1989b). Pow. Diff. 4(4), 220–222.CrossRefGoogle Scholar
Blanchard, F.N. (1989c). Pow. Diff. 4(4), 227–230.CrossRefGoogle Scholar
Blanchard, F.N. & Saligan, P.P. (1989). Pow. Diff. 4(1), 26–28.CrossRefGoogle Scholar
Castro, A., Rasines, I., Sánchez-Martos, M.C., García-Casado, P. (1988). Pow. Diff. 3(4), 219–221.CrossRefGoogle Scholar
Huang, T.C., Karimi, R., Baumert, J.-C. & Bjorklund, G.C. (1988). Pow. Diff. 3(2), 78–80.CrossRefGoogle Scholar
Huang, T.C., Nazzal, A.I., Tokura, Y., Torrance, J.B., Karimi, R. (1988). Pow. Diff. 3(2), 81–83.CrossRefGoogle Scholar
Klug, H.P., & Alexander, L.E. (1974). X-ray Diffraction Procedures For Polycrystalline and Amorphous Materials, 2nd ed. New York: John Wiley & Sons.Google Scholar
Lowe-Ma, C. K. (1990). Pow. Diff. 5(4), 223–224.CrossRefGoogle Scholar
Lowe-Ma, C.K. & Decker, D.L. (1986). Acta Crystallogr. C42, 1648–1649.Google Scholar
Lowe-Ma, C.K., Nissan, R.A., Wilson, W.S., Houk, K.N. & Wang, X. (1988). J. Chem. Research (M), 1740–1760.Google Scholar
Acta Crystallogr. C42 (1988). J. Chem. Research (S), 214–215.Google Scholar
McCarthy, G.J. and Welton, J.M. (1989). Pow. Diff. 4(3), 156–159.CrossRefGoogle Scholar
McCarthy, G.J. (1989). Private communication to ICDD Task Group.Google Scholar
Meyer, R. (1987). Explosives, 3rd ed. New York: VCH Publishers.Google Scholar
Schreiner, W.N. and Kimmel, G. (1987). Adv. X-ray Analysis 30, 351–356.Google Scholar
Smith, D.K., Nicols, M.C. & Zolensky, M.E. (1982). POWD10, A FORTRAN Program for Calculating X-ray Powder Diffraction Patterns, version supplied by Scintag, Inc.Google Scholar
Smith, G.S. & Snyder, R.L. (1979). J. Appl. Crystallogr. 12. 60–65.CrossRefGoogle Scholar
Snyder, R.L. (1983). Adv. X-ray Analysis 26, 1–9. New York: Plenum.Google Scholar
SHELXTL (1984). Version 4.1, Nicolet XRD (G. Sheldrick).Google Scholar
Wilson, A.J.C. (1963). Mathematical Theory of X-ray Powder Diffractometry. New York: Gordon and Breach, Science Publishers.Google Scholar