Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T22:18:33.398Z Has data issue: false hasContentIssue false
  • English
  • Français

Hypothesis testing with error correction models

Published online by Cambridge University Press:  21 July 2021

Patrick W. Kraft ,
Ellen M. Key  and
Matthew J. Lebo Open the ORCID record for Matthew J. Lebo [Opens in a new window]
Patrick W. Kraft
Affiliation:
University of Wisconsin-Milwaukee, Milwaukee, WI, USA
Ellen M. Key
Affiliation:
Appalachian State University, Boone, NC, USA
Matthew J. Lebo*
Affiliation:
University of Western Ontario, London, ON, Canada
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Grant and Lebo (2016) and Keele et al. (2016) clarify the conditions under which the popular general error correction model (GECM) can be used and interpreted easily: In a bivariate GECM the data must be integrated in order to rely on the error correction coefficient, $\alpha _1^\ast$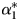, to test cointegration and measure the rate of error correction between a single exogenous x and a dependent variable, y. Here we demonstrate that even if the data are all integrated, the test on $\alpha _1^\ast$ 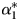is misunderstood when there is more than a single independent variable. The null hypothesis is that there is no cointegration between y and any x but the correct alternative hypothesis is that y is cointegrated with at least one—but not necessarily more than one—of the x's. A significant $\alpha _1^\ast$ 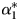can occur when some I(1) regressors are not cointegrated and the equation is not balanced. Thus, the correct limiting distributions of the right-hand-side long-run coefficients may be unknown. We use simulations to demonstrate the problem and then discuss implications for applied examples.

Keywords

Time series models
Type
Research Note
Information
Political Science Research and Methods , Volume 10 , Issue 4 , October 2022 , pp. 870 - 878
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of the European Political Science Association

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Banerjee, A, Dolado, JJ, Galbraith, JW and Hendry, D (1993) Co-Integration, Error Correction, and the Econometric Analysis of Non-Stationary Data. Oxford: Oxford University Press.CrossRefGoogle Scholar
Bårdsen, G (1989) Estimation of long run coefficients in error correction models. Oxford Bulletin of Economics and Statistics 51, 345–350.CrossRefGoogle Scholar
Box-Steffensmeier, JM, Freeman, JR, Hitt, MP and Pevehouse, JCW (2014) Time Series Analysis for the Social Sciences. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Calderia, GA and Zorn, C (1998) Of time and consensual norms in the supreme court. American Journal of Political Science 42, 874–902.CrossRefGoogle Scholar
Clarke, HD and Stewart, MC (1995) Economic evaluations, prime ministerial approval and governing party support: rival models reconsidered. BJPS 25, 145–170.Google Scholar
DeBoef, S and Keele, L (2008) Taking time seriously. American Journal of Political Science 52, 184–200.CrossRefGoogle Scholar
Enders, W (2015) Applied Econometric Time Series, 4th Edn. New York: Wiley.Google Scholar
Engle, RF and Granger, CWJ (1987) Co-integration and error correction: representation, estimation, and testing. Econometrica 55, 251–276.CrossRefGoogle Scholar
Enns, PK (2014) The public's increasing punitiveness and its influence on mass incarceration in the United States. American Journal of Political Science 58, 857–872.CrossRefGoogle Scholar
Enns, PK and Wlezien, C (2017) Understanding equation balance in time series regression. The Political Methodologist 24, 2–12.Google Scholar
Enns, PK, Kelly, NJ, Masaki, T and Wohlfarth, PC (2016) Don't jettison the general error correction model just yet: a practical guide to avoiding spurious regression with the GECM. Research & Politics 3, 2053168016643345.CrossRefGoogle Scholar
Ericsson, NR and MacKinnon, JG (2002) Distributions of error correction tests for cointegration. The Econometrics Journal 5, 285–318.CrossRefGoogle Scholar
Grant, T and Lebo, MJ (2016) Error correction methods with political time series. Political Analysis 24, 3–30.CrossRefGoogle Scholar
Harbo, I, Johansen, S, Neilsen, B and Rahbek, A (1998) Asymptotic inference on cointegrating rank in partial systems. Journal of Business and Economic Statistics 4, 388–399.Google Scholar
Johansen, Søren (1988) Statistical analysis of cointegration vectors. Journal of economic dynamics and control 12, 231–254.CrossRefGoogle Scholar
Johansen, Søren (1995) Likelihood-Based Inference in Cointegrated Vector Autoregressive Models. Oxford: Oxford University Press.CrossRefGoogle Scholar
Keele, L, Linn, S and Webb, CM (2016) Treating time with all due seriousness. Political Analysis 24, 31–41.CrossRefGoogle Scholar
Kelly, NJ and Enns, PK (2010) Inequality and the dynamics of public opinion: the self-reinforcing link between economic inequality and mass preferences. American Journal of Political Science 54, 855–870.CrossRefGoogle Scholar
Lebo, MJ and Grant, T (2016) Equation balance and dynamic political modeling. Political Analysis 24, 69–82.CrossRefGoogle Scholar
Lebo, MJ and Kraft, PW (2017) The general error correction model in practice. Research & Politics 4, 1–13.CrossRefGoogle Scholar
Lebo, M and Norpoth, H (2011) Yes, prime minister: the key to forecasting British elections. Electoral Studies 30, 258–263.CrossRefGoogle Scholar
Lebo, MJ and Young, E (2009) The comparative dynamics of party support in Great Britain: Conservatives, Labour and the Liberal Democrats. Journal of Elections, Public Opinion and Parties 19, 73–103.CrossRefGoogle Scholar
Ostrom, CW Jr and Smith, R (1993) Error correction, attitude persistence, and executive rewards and punishments: a behavioral theory of presidential approval. Political Analysis 4, 127–184.CrossRefGoogle Scholar
Pickup, M and Kellstedt, PM (2018) Equation Balance in Time Series Analysis: What It Is and How to Apply It. Working Paper.Google Scholar
Ramirez, MD (2009) The dynamics of partisan conflict on congressional approval. American Journal of Political Science 53, 681–694.CrossRefGoogle Scholar
Sims, CA, Stock, JH and Watson, MW (1990) Inference in linear time series models with some unit roots. Econometrica 58, 113–144.CrossRefGoogle Scholar
Stock, JH and Watson, MW (1993) A simple estimator of cointegrating vectors in higher order integrated systems. Econometrica 61, 783–820.CrossRefGoogle Scholar
Ura, JD (2014) Backlash and legitimation: macro political responses to supreme court decisions. American Journal of Political Science 58, 110–126.CrossRefGoogle Scholar
Ura, JD and Wohlfarth, PC (2010) “An Appeal to the People”: public opinion and congressional support for the supreme court. Journal of Politics 72, 939–956.CrossRefGoogle Scholar
Volscho, TW and Kelly, NJ (2012) The rise of the super-rich power resources, taxes, financial markets, and the dynamics of the top 1 percent, 1949 to 2008. American Sociological Review 77, 679–699.CrossRefGoogle Scholar
Webb, CM, Linn, S and Lebo, MJ (2019) A bounds approach to inference using the long run multiplier. Political Analysis 27, 281–301.CrossRefGoogle Scholar
Webb, CM, Linn, S and Lebo, MJ (2020) Beyond the unit root question: uncertainty and inference. American Journal of Political Science 64, 275–292.CrossRefGoogle Scholar
Supplementary material: Link

Kraft et al. Dataset

Dataset

https://doi.org/10.7910/DVN/ESTHIJ
Link
Supplementary material: PDF

Kraft et al. supplementary material

Kraft et al. supplementary material

Download Kraft et al. supplementary material(PDF)
PDF 198.4 KB