International crises often place political leaders in domestic jeopardy. Sanctions for failure range from loss of office to death. Unsurprisingly, it has become a commonplace of international relations scholarship that leaders act with one eye on retaining domestic support (Snyder, Reference Snyder1991; Bueno de Mesquita et al., Reference Bueno de Mesquita, Morrow, Siverson and Smith1992; Fearon, Reference Fearon1994a; Smith, Reference Smith1998; Goemans, Reference Goemans2000; Schultz, Reference Schultz2001a; Debs and Goemans, Reference Debs and Goemans2010). Two prominent literatures suggest strategies citizens could adopt to optimally exploit leaders’ interest in retention.
One literature emphasizes audience costs. Fearon (Reference Fearon1994a) observes that a domestic audience can encourage resolve, enhancing a leader's bargaining posture. In the canonical version, a leader pays a domestic cost after backing down from fighting in a crisis they themselves initiated. Anticipating this cost, only leaders with high values for fighting initiate crises, credibly influencing a target's beliefs about their own war payoff.
The other literature emphasizes political bias (Bueno de Mesquita and Lalman, Reference Bueno de Mesquita and Lalman1992; Bueno de Mesquita et al., Reference Bueno de Mesquita, Morrow, Siverson and Smith1992; Jackson and Morelli, Reference Jackson and Morelli2007). These authors argue that leaders will typically want to fight in circumstances the citizens would not. This could be because leaders themselves do not bear the physical costs of fighting, or because they expect to appropriate a disproportionate share of the rewards of victory. Domestic consequences for belligerent foreign policy decisions reduce the leader's crisis and war payoffs, leading to more peace and fewer challenges. This political bias is an example of the incentive problems studied in the political agency literature.Footnote 1 As such, domestic consequences for belligerent foreign policy decisions could reduce the leader's crisis and war payoffs, leading to more peace and fewer challenges.Footnote 2
In this paper, we present a model that captures concerns from both strands of the literature, and characterize the optimal retention strategy.Footnote 3 Our contribution characterizes the citizen's optimal retention strategy when a ruler engages in a simple form of crisis bargaining, allowing us to endogenize the domestic political constraints that have played a large role in recent international relations theory. These political constraints are sensitive to two different parts of the agency problem. The first, which is well-explored in the literature, is the divergence between the leader's private payoff to war and the citizens’ payoffs to war. The second, which to our knowledge is new, is a commitment problem faced by the leader. This commitment problem comes from the fact that committing to keep the status quo unless the private information received by the leader is quite favorable for Home's prospects in war leads to high appeasement offers in the case of initiation. But those same high offers make it attractive to initiate a crisis when their signal is not so favorable.Footnote 4
The optimal response to this commitment problem for the citizen is quite robust: the leader should always face a lower probability of retention after backing down than if she keeps the status quo. This allows a citizen to manage the leader's incentive to initiate crises under unfavorable circumstances. But how exactly to offset the leader's political bias is more sensitive to the environment. When total costs of war are low, the optimal scheme offsets the leader's political bias by rewarding backing down more than going to war. This leads the leader to fully internalize the costs of fighting, an action she nonetheless takes with positive probability in the equilibrium. When total costs of fighting are large, on the other hand, the optimal scheme leads to peace with probability one. In this case, the citizen enhances the bargaining power of the leader by punishing her for backing down rather than fighting.
We proceed by building on the standard crisis model with two countries that we call Home and Foreign (Bueno de Mesquita and Lalman, Reference Bueno de Mesquita and Lalman1992; Fearon, Reference Fearon1994b; Schultz, Reference Schultz1999). In the crisis, the Home leader cares both about the crisis outcome and about being retained as leader. Citizens decide whether to retain the leader. This creates a political agency model of foreign policy decisions with moral hazard, in the canonical form of Barro (Reference Barro1973), Ferejohn (Reference Ferejohn1986), and Austen-Smith and Banks (Reference Austen-Smith and Banks1989).
We analyze the model under two different assumptions about citizens. First, we assume that citizens have limited ability to assess detailed policy outcomes. Citizens observe crisis initiation and the fact of settlement, but not the settlement's details. This might reflect the lack of attention citizens pay to foreign policy, citizens’ bounded rationality, or that settlement details are secret. Then we reconsider the model under the assumption that citizens observe the full details of the settlement. This might reflect a substantive setting in which a settlement resets territorial boundaries.
A key feature of our setup is the flexibility in how citizens can punish the leader. The citizens might punish the leader for backing down, relative to the status quo. That is, the retention probability can be lower for a leader who settles a crisis than for a leader who stays out of the crisis in the first place. This is like the audience cost in Tomz's (Reference Tomz2007) survey experiments. The citizens also might punish the leader for backing down, relative to escalating. That is, the retention probability can be lower for a leader who settles a crisis than for a leader who rejects the settlement in favor of fighting. This is like the audience costs in Fearon's (Reference Fearon1994a) a war of attrition model. IR scholars often treat these two notions of punishment interchangeably, but they play importantly different roles in our analysis.
In a paper written independently and simultaneously, Kertzer and Brutger (Reference Kertzer and Brutger2016) introduce a very similar distinction. In an experimental study, they distinguish between an inconsistency cost that domestic audiences levy on leaders (they refer to this as the audience cost) and a belligerence cost that audiences impose on leaders who get involved in conflicts at all. They ground these two costs in an argument from political psychology and highlight heterogeneity among the citizens. Our model, by contrast, retains the citizen homogeneity assumption traditional in the audience cost literature, and focuses on the way these two different costs can be optimally used.
Our results help sort out the foundations of the literature on audience costs. Fearon, in his seminal paper, gave an informal optimality-based defense of the assumption:
The [audience cost] results here suggest that …, if the principal [citizen] could design a ‘wage contract’ for the foreign policy agent, the principal would want to commit to punishing the agent for escalating a crisis and then backing down. (Fearon, Reference Fearon1994a, p. 581)
While plausible, this defense has not convinced all scholars. For example, Schultz asked:
[w]hy voters would punish their leaders for getting caught in a bluff, if bluffing is sometimes an optimal strategy. After all, anyone who has ever played poker understands that bluffing is not always undesirable behavior. … Clearly, additional work remains to be done on why and under what conditions rational voters would impose audience costs. (Schultz, Reference Schultz1999, p. 237, ft. 11)
We directly take on this question of what citizens would ideally commit to in punishment. We show both conditions under which Fearon's intuition is right, and the limits of that intuition.Footnote 5
This modeling of audience costs in a political agency setting addresses an important criticism of audience cost theory. As Snyder and Borghard (Reference Snyder and Borghard2011) emphasize, citizens’ policy preferences, be they hawkish or dovish, need to be central to any theoretical explanation of how voters respond to a leader's foreign policy. A similar argument is made by Debs and Weiss (Reference Debs and Weiss2016) that voters punish inappropriate, not inconsistent policies. We do not assume that citizens care directly about consistency between threats and military action. We also do not assume that threats are unambiguous commitments by the leader. Citizens know at the outset that some threats will be followed by an agreement with the foreign rival.
Our results speak to extensive literatures in international relations and comparative politics investigating the empirical evidence for, and microfoundations of, audience costs. Early attempts to assess Fearon's (Reference Fearon1994a) hypothesis about democracies’ greater ability to generate audience costs were generally positive (Eyerman and Hart, Reference Eyerman and Hart1996; Partell and Palmer, Reference Partell and Palmer1999; Gelpi and Griesdorf, Reference Gelpi and Griesdorf2001; Haynes, Reference Haynes2012). But subsequent analyses have complicated the picture regarding variation across regime type (Weeks, Reference Weeks2008, Reference Weeks2012; Kurizaki and Whang, Reference Kurizaki and Whang2015; Crisman-Cox and Gibilisco, Reference Crisman-Cox and Gibilisco2018), domestic political structures (Prins, Reference Prins2003; Potter and Baum, Reference Potter and Baum2014), and leader gender (Schwartz and Blair, Reference Schwartz and Blair2020). While we do not explicitly model regime type, we can think about two different elements of regime type with our model. First, there is the issue of political bias. Specifically, how far can a leader and citizens preferences over war and peace diverge? One might conjecture these biases are necessarily smaller in more representative regimes. Second, the kinds of retention strategies that are feasible in a given regime also matter for the likelihood of war and peace.
There is also a large, recent experimental literature on audience costs that explores how leaders’ interpretation of audience costs vary (Yarhi-Milo et al., Reference Yarhi-Milo, Kertzer and Renshon2018), and how partisanship and policy preferences exacerbate or mitigate audience cost effects (Trager and Vavreck, Reference Trager and Vavreck2011; Levy et al., Reference Levy, McKoy, Poast and Wallace2015; Kertzer and Brutger, Reference Kertzer and Brutger2016). Whether the behavior in these experiments is rational or irrational, or whether they represent sophisticated strategic actions or behavioral responses, cannot be inferred without a well-defined theory of political agency. Our approach is explicitly rational and, at a minimum, we provide a necessary benchmark for interpreting these and other studies. As we argue below, we think this approach goes beyond simply being a benchmark and provides a new understanding of how a rational electorate should behave, when that behavior will look like traditional audience costs, and when it will not.
1. The model
There are two countries, Home and Foreign. Foreign is a unitary actor, but Home is made up of a leader, who makes international decisions, and a citizen who decides whether or not to retain the leader.
The countries share a divisible unit of resource, with Home's status quo share y and Foreign's status quo share 1 − y. At the outset, Home has the option to keep the status quo or to demand more, initiating a crisis. If Home initiates, Foreign gets to propose either war or a new allocation of shares, (x, 1 − x), with 0 ≤ x ≤ 1. If Foreign proposes an allocation and Home accepts it, then that allocation is implemented. If Foreign proposes war or if Home rejects Foreign's proposal, there is a war. This war costs Home's citizen c H and Foreign c F, and the winner takes all the resource. We summarize this in the game tree of Figure 1
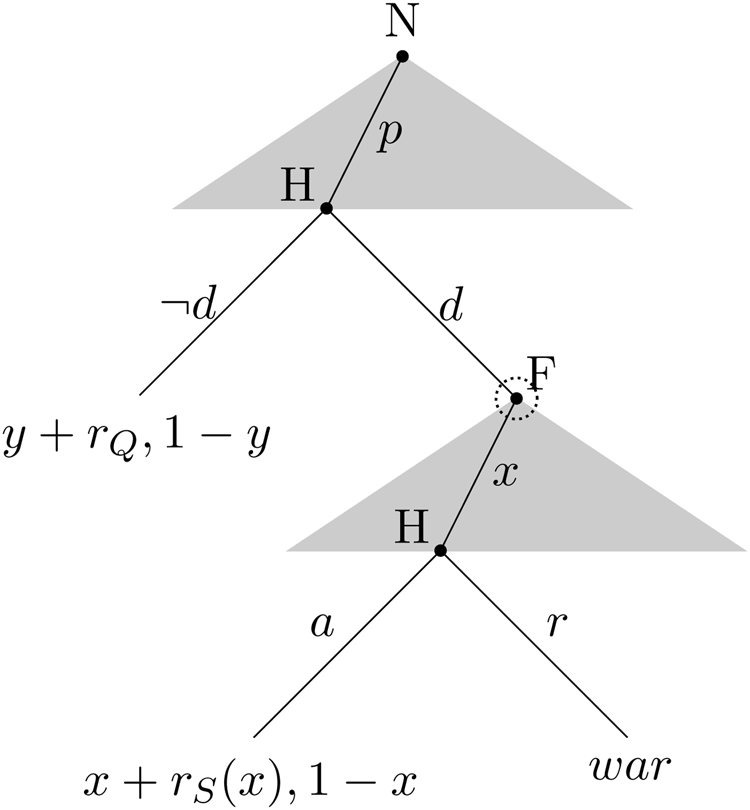
Fig. 1. Tree for the game between the Home Leader and Foreign. Nature moves at the root; the Home Leader's actions are labeled as follows: d denotes a demand, ¬d denotes no demand, a denotes accepting an offer, and r denotes rejecting an offer. The information set of Foreign represents ignorance of Nature's move. War payoffs are p − γc H + r W, $1-{\opf E}[ p\vert \sigma _H( p) ] -c_F$![]() .
.
We assume that c H ≤ 1 − y and c F ≤ 1 − y. That is, Home's cost of war is less than the maximum it could get from Foreign in war, and Foreign's cost of war is not so high that it would rather give up its share than fight to keep it.
In a war, the winner is determined by the relative strengths of the countries. No player knows this quantity for sure. Without loss of generality, the Home leader gets a signal p ∈ [0, 1], which we can interpret as his posterior probability of victory in war. The prior distribution of this posterior probability is uniform on [0, 1].Footnote 6
After the crisis, the Home citizen retains or dismisses the Home leader. We consider two different specifications of what the citizen's response can be based upon. In the case of secret settlements, the citizen observes whether the Home leader kept the status quo and, if not, whether a settlement was reached or a war was fought. This could occur because the agreements were in fact secret, because the citizens doesn't pay attention, or because the citizen are boundedly rational and cannot condition their actions on the details of the agreement. In the case of public settlements, by contrast, the Home citizen observes the precise allocation that a settlement calls for.Footnote 7
Everyone evaluates outcomes based on the final allocation of the resource and whether or not there is a war; in addition, the Home leader prefers retaining office to losing it. To specify payoffs formally, we use the following notation: π is Home's final share of the resource, w is an indicator function taking the value 1 if there is a war and zero otherwise, and ρ is an indicator function taking the value 1 if the leader is retained and 0 otherwise. Foreign ranks outcomes according to the expectation of (1 − π) − wc F; the Home citizen ranks outcomes according to the expectation of π − wc H; and the Home leader ranks outcomes according to the expectation of π − wγc H + ρ, where γ is a parameter less than or equal to 1. Like leaders in selectorate theory (Bueno de Mesquita et al., Reference Bueno de Mesquita, Morrow, Siverson and Smith1992) and models of audience costs (Ramsay, Reference Ramsay2004; Tarar and Leventoğlu, Reference Tarar and Leventoğlu2013; Debs and Weiss, Reference Debs and Weiss2016) leaders care about both domestic and international outcomes.The game's key notation is in Table 1.
Table 1. Key notation

For a fixed reward strategy to be followed by the citizen, there is an extensive form game of incomplete information played between the leader of Home and Foreign. We first fix an arbitrary retention strategy and characterize the perfect Bayesian equilibria of this game. Then, following the lead of Fearon (Reference Fearon1999), we characterize the reward strategy whose associated equilibrium maximizes the citizen's ex ante payoff.
We focus on equilibria of a particularly simple form. Say that a strategy for the Home leader is monotone if:
(i) Home initiates with signal p′ and p > p′ together imply that Home initiates with signal p, and
(ii) Home rejects offer x′ with signal p′ and p > p′ together imply that Home rejects offer x′ with signal p.
We will study perfect Bayesian equilibrium in which the Home leader's strategy is monotone. Lemma 1 (below) implies that any PBE satisfies the second condition, but there might be equilibria that involve non-monotone entry decisions. However, these profiles would not be equilibria if the model were modified so that entry always carried some very small risk of war, independent of the settlement proposed by Foreign. Thus we focus on monotone equilibria for the remainder of the analysis.
Formally, a monotone assessment is a profile $( ( \underline {p},\; \, \overline {p}({\cdot}) ) ,\; \, ( \mu ,\; \, x) )$![]() , where:
, where:
• the Home leader initiates if p ≥ p,
• the Home leader accepts offer x′ if $p\leq \overline {p}( x')$
 ,
,• Foreign believes that a Home leader who initiates has p distributed uniformly on [μ, 1],
• Foreign offers x.
A monotone assessment is a monotone equilibrium if:
• the strategy profile $( \underline {p},\; \, \overline {p}({\cdot}) ,\; \, x)$
 is sequentially rational given beliefs μ, and
is sequentially rational given beliefs μ, and• μ = p.
Recall that the citizen is not a player in the game; instead she follows an exogenous retention strategy. Such a strategy is given by a tuple of retention probabilities r = (r Q, r S, r W), representing the probability that the citizen retains the Home leader under the status quo, settlement, and war, respectively. (In the case of public settlements, r S is a function from [0, 1] to [0, 1].) Write ${\cal E}( {\bf r})$![]() for the set of strategy profiles associated with monotone equilibria of the game induced by r.
for the set of strategy profiles associated with monotone equilibria of the game induced by r.
We will use the following terminology to describe the qualitative features of retention strategies. A retention strategy punishes backing down relative to fighting if r W > r S. A retention strategy punishes backing down relative to the status quo if r Q > r S.
1.1 Interpreting the assumptions
Before turning to the analysis, five of our assumptions require further comment.
First, the Home leader's payoff depends on both the crisis outcome and on whether she is retained in office. Both components are critical for a nontrivial incentive problem. Without any concern for retention, the Home leader will be completely unresponsive to incentives. Without any concerns for what happens in the crisis, the Home leader will be indifferent across all strategies that lead to the same retention probability, so a constant retention probability can provide optimal incentives.
The parameter γ in the Home leader's payoff measures the degree to which the leader and the citizen have a conflict of interest in crisis outcomes. Such conflicts make the leader more eager than the citizen to initiate a war. This is natural when the leader has full access to the spoils of war but does not do the actual fighting (e.g., Bueno de Mesquita et al., Reference Bueno de Mesquita, Siverson and Woller1992; Goemans, Reference Goemans2000; Chiozza and Goemans, Reference Chiozza and Goemans2004). Differences in γ may also reflect institutional differences—compulsory, universal military service, for example, should induce high values of γ (at least for leaders with combat-aged children), while an all-volunteer military might insulate leaders more from the costs of war. Either way, divergent preferences between citizens and leaders is key to our model.
Second, we will think of c H + c F as the total cost of war. This might seem to ignore the Home leader's cost of war, but we want to avoid taking the three player structure that literally. Instead, we interpret each country as a unit mass of citizens, with c H and c F the per capita costs of fighting. The Home leader bears a lower cost than the average citizen, captured by γ. Because she is only one person in a large population, per capita costs are unaffected.
Third, the assumption of private settlements captures any setting in which citizens cannot condition on the full details of settlements. This is certainly the case when those details are literally unobservable, as is the case for classified concessions of the sort involved in the Cuban missile crisis. But the assumption can also capture settings in which citizens can observe the settlement, but do not know enough to evaluate it. For example, citizens will have a hard time evaluating the consequences of detailed nuclear negotiations. Citizens may also face costs for learning about the agreement, may have limited attention, or use settlement or conflict as political cues. But regardless of the cause, the incentive problem is the same.
Fourth, if a war is fought, we do not allow the citizen to condition retention on which side wins. Although it would be more natural to assume that the citizen can also observe the outcome of a war, we argue in the supplementary Appendix that there is no real loss of substantive insight from ignoring this possibility.
The key reason we can ignore the winning and losing of wars is that the citizen in our model actually benefits from rewarding the leader for losing the war. Intuitively, this gives a relatively weak type a kind of insurance policy against adverse war outcomes. Insurance makes her more willing to fight, which, in turn, increases the offer Foreign is willing to make.
In our view, this result leans too heavily on the fact that the war outcome does not depend on any action of the Leader. If outcomes did depend on fighting decisions, rewarding losers would create a moral hazard problem that would work against the citizen's interest. As such, a reasonable model that allowed for different retention probabilities for winners and losers would involve a constraint to ensure that winners are retained with at least as high a probability as losers. With such a constraint, the optimum reward scheme will result in the same reward for winners and losers. To keep the notation simple, we have simply imposed that equality in the main text.
Fifth, we take the informational environment—secret or public settlements—as exogenous. Several scholars argue that the canonical audience cost mechanism is problematic when leaders can manipulate the interpretation and transmission of their actions during crisis bargaining (Slantchev, Reference Slantchev2006; Bloch-Elkon, Reference Bloch-Elkon2007; Levendusky and Horowitz, Reference Levendusky and Horowitz2012; Downes and Sechser, Reference Downes and Sechser2012). We recognize the importance of this concern, but adding an option for the Home leader to manipulate the citizen's information to the already complex optimization problem here is beyond the scope of this paper.
2. Secret settlements: crisis equilibrium
It's easiest to start with the case of secret settlements. We will handle this is two steps. First, we characterize equilibrium for an arbitrary retention rule. Then the following section characterizes the retention rule that leads to the best equilibrium for the Home citizen. Our analysis will show that voters desire for favorable outcomes may lead them to reward inherently disliked outcomes and punish favored outcomes because of their strategic consequences. Lacking a theoretical understanding of the political agency problem, there is no simple way to relate voters’ underlying preferences over the various crisis outcomes and their retention actions.
So let r = (r Q, r S, r W) ∈ [0, 1] 3 be arbitrary. How will the crisis unfold?
Start at the end of the game. Home will accept the offer (x, 1 − x) exactly when x + r S ≥ p + r W − γc H. Solve this to establish:
LEMMA 1 Home accepts x if and only if
Next, we consider Foreign's optimal offer. In a monotone equilibrium, Foreign believes that, conditional on initiating, Home's signal is uniform on [μ, 1], for some μ. So if Foreign offers (x, 1 − x), its payoff is
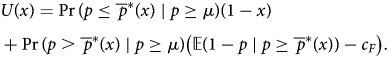
The first term is the settlement times the probability of acceptance, while the second term is the expected payoff conditional on wartimes the complementary probability.
The function U breaks naturally into three components:
(i) If x ≥ 1 − (r S − r W) − γc H, the offer is accepted for sure, and U(x) = 1 − x.
(ii) If x ≤ μ − (r S − r W) − γc H, the offer is rejected for sure, and $U( x) = 1-{\opf E}( p\mid p\geq \mu ) -c_F$
 , a constant.
, a constant.(iii) If μ − (r S − r W) − γc H < x < 1 − (r S − r W) − γc H, both acceptance and war have positive probability and U is equal to the quadratic function:
$$Q( x) = ( 1-x) \int_{\mu}^{\overline{\,p}( x) }{dt\over 1-\mu} + \int_{\overline{\,p}( x) }^{1} ( 1-t-c_F ) {dt\over 1- \mu}.$$
The basic idea of the optimal offer is then clear. It would be foolish to offer more than 1 − (r S − r W) − γc H. Doing so would amount to giving additional resources to an opponent who was going to accept anyway. Given that upper bound, the offer should maximize Q. We then have:
LEMMA 2 Let
(i) If x* > μ − (r S − r W) − γc H, then x* is the unique optimal offer.
(ii) If x* ≤ μ − (r S − r W) − γc H, then any x ≤ μ − (r S − r W) − γc H is an optimal offer. In particular, x* is optimal.
(Proofs omitted from the main text are in the Appendix.)
Given an equilibrium offer (x*) and private information (p), we can calculate Home's continuation value of starting a crisis, J, as
This function is graphed in Figure 2. The dashed lines represent Home's utilities to settlement and war as a function of their private information about success in war. Home will enter if J(p, x*) > y + r Q, will not enter if J(p, x*) < y + r Q, and is indifferent if J(p, x*) = y + r S. As an immediate implication, we have:
LEMMA 3 In any equilibrium in which there is positive probability that Home keeps the status quo and positive probability that Home enters and accepts the offer,
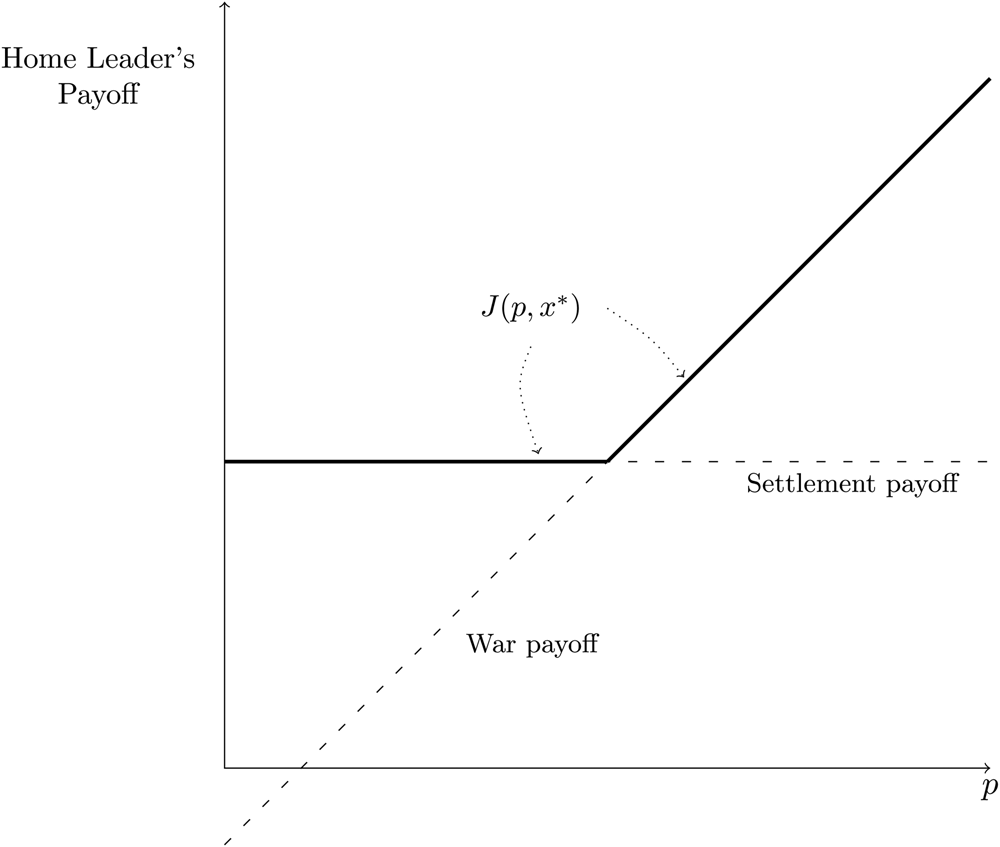
Fig. 2. J(p, x*), in bold, is the upper envelope of the Home leader's payoffs to settlement, x* + r S, and to war, p − γc H + r W.
Intuitively, if this equality did not hold, then all types who do not fight would either enter and accept when x* + r S > y + r Q or all such types would stay out when x* + r S < y + r Q. But then there would be no equilibrium where Home both enters and accepts with positive probability and also keeps the status quo with positive probability. The citizen's retention strategy resolves the leader's incentive to pool on entry and allows the Home country to do better in bargaining. That is, it commits the leader to initiate a crisis only when it is sufficiently strong and, as Lemma 3 demonstrates, this is always a source of one form of audience cost.
Constructive arguments can be used to establish that, for any r, there exists a pure-strategy monotone equilibrium. Rather than characterize this entire equilibrium correspondence, we ask: which is optimal?
3. Secret settlements: optimal retention
In the principal-agent framework, the link between voter strategies and leader behavior is shaped by the desire to create incentives that get voters the best expected outcome ex ante, which does not inherently imply a preference for “consistency.” In fact, sometimes voters will want to incentivize behavior they dislike because of the strategic consequences. As we will see, these incentives to control leaders create some behavior that is an audience cost, even though the strategy is rooted in rational policy preferences.
The retention strategy that is best for the Home citizen is the one that induces an equilibrium maximizing the citizen's ex ante payoff. Write p for the least type that initiates, x for the offer, and $\overline {p}$![]() for the least type that fights. Then the citizen's expected payoff is
for the least type that fights. Then the citizen's expected payoff is
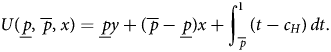
The first term is the probability that Home keeps the status quo times Home's status quo share, the second term is the probability that Home's leader initiates a crisis and then accepts the appeasement offer times the value of that offer, and the third term is the expected payoff on the event that there is war. We do not rule out the possibility that $\underline {p} = \overline {p}$![]() or that one or both of the cutpoints is 0 or 1, so this payoff function covers all the cases discussed above.
or that one or both of the cutpoints is 0 or 1, so this payoff function covers all the cases discussed above.
3.1 Incentives for fixed x
As a benchmark, it's helpful to calculate the optimal strategy when x is fixed. If, for example, the citizen does not realize that their retention strategy affects the bargaining strategy of Foreign, they would believe this to be the optimal retention scheme. Here, the only problem the citizen needs to solve is the discrepancy between her cost of fighting and the leader's cost of fighting. Comparing this solution to the full solution discussed below will highlight the role of strategic bargaining between Home and Foreign in shaping incentives.
Start at the accept/reject decision. The citizen gets p − c H from rejection and x from acceptance. Thus, the appropriate critical type for acceptance is the type that makes the citizen indifferent: p* = x* + c H. We can make the leader implement this rule by setting r S − r W = (1 − γ) c H. This retention differential makes the ruler exactly internalize the extra cost borne by the citizen in the case of war.
Now roll back to the entry decision. Write the continuation value for the game conditional on choosing to enter as $\hat {J}( p,\; \, x^{\ast }) = \max \langle x^{\ast },\; \, p-c_H\rangle$![]() . The citizen would not enter if and only if $y\geq \hat {J}( p,\; \, x^{\ast })$
. The citizen would not enter if and only if $y\geq \hat {J}( p,\; \, x^{\ast })$![]() . To ensure that the leader of Home does exactly what the citizen would do at each instance, it suffices to take r Q − r S = 0 and r S − r W = (1 − γ) c H. Such a strategy looks like this: choose any number κ ∈ [(1 − γ) c H, 1], and set r Q = r S = κ and r W = κ − (1 − γ) c H.
. To ensure that the leader of Home does exactly what the citizen would do at each instance, it suffices to take r Q − r S = 0 and r S − r W = (1 − γ) c H. Such a strategy looks like this: choose any number κ ∈ [(1 − γ) c H, 1], and set r Q = r S = κ and r W = κ − (1 − γ) c H.
In this benchmark, r S > r W—the citizen rewards settlement relative to war. This is a direct response to the leader's political bias. It can be thought of as a scheme that results in an apparently “dovish electorate.”
Things get more interesting when the offer is not fixed. Then, the Home leader's incentives can also be used to affect the other state's behavior. The optimal retention strategy responds to exactly that incentive: the offer x* is manipulated through the choice of r. Recall that
The two arguments of the max represent two different ways the Home citizen can manipulate x*. If some offers are rejected, then the citizen can manipulate x* only by changing the critical type who enters. If all offers are accepted, the Home citizen can manipulate the offer by changing r S − r W. The citizen's ex ante optimal incentive strategy balances these two considerations.
3.2 The full optimum
Given this basic understanding of the ways the citizen wants to shape the leader's incentives and manipulate the equilibrium of the game, we can think about the citizen's optimal retention strategy in this light.
To characterize optimal retention strategy, we maximize the citizen's payoff (given by (2)), subject to the constraints:
(i) the retention rule is feasible: r ∈ [0, 1] 3,
(ii) the strategies are feasible: p ∈ [0, 1], x ∈ [0, 1], and $\overline {p}( x) \in [ 0,\; \, 1]$
 for all x ∈ [0, 1], and
for all x ∈ [0, 1], and(iii) the strategies of H and F are part of an assessment that is a equilibrium: there is a μ such that $( ( \underline {p},\; \, \overline {p}({\cdot}) ) ,\; \, ( x,\; \, \mu ) ) \in {\cal E}( {\bf r})$
 .
.
Let ${\cal F}$![]() denote the set of $( {\bf r},\; \, \underline {p},\; \, \overline {p}({\cdot}) ,\; \, x)$
denote the set of $( {\bf r},\; \, \underline {p},\; \, \overline {p}({\cdot}) ,\; \, x)$![]() satisfying the first two constraints, then consider the citizen's Program:
satisfying the first two constraints, then consider the citizen's Program:
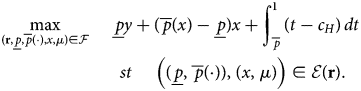
A retention strategy r is optimal if there is an equilibrium $( ( \underline {p},\; \, \overline {p}({\cdot}) ) ,\; \, ( x,\; \, \mu ) )$![]() such that $( {\bf r},\; \, \underline {p},\; \, \overline {p}({\cdot}) ,\; \, x,\; \, \mu )$
such that $( {\bf r},\; \, \underline {p},\; \, \overline {p}({\cdot}) ,\; \, x,\; \, \mu )$![]() solves Program 3.
solves Program 3.
A couple of remarks on uniqueness will help us interpret the following Proposition. First, there is no guarantee that there is a unique equilibrium in the game defined by a retention strategy. When there are multiple equilibria at r, the maximization program entails choosing the equilibrium from ${\cal E}( {\bf r})$![]() that maximizes (2). To reflect this, we refer to behavior in the best equilibrium induced by r. (That behavior is uniquely determined.) Second, there are typically many retention strategies that lead to a given citizen payoff in their best induced equilibrium. To reflect this, the statements in the Proposition describe the full set of retention strategies that are optimal.
that maximizes (2). To reflect this, we refer to behavior in the best equilibrium induced by r. (That behavior is uniquely determined.) Second, there are typically many retention strategies that lead to a given citizen payoff in their best induced equilibrium. To reflect this, the statements in the Proposition describe the full set of retention strategies that are optimal.
Proposition 1
(i) Suppose 2c H + c F < 1 − y. Then a retention strategy is optimal if and only if it is of the form
$$\matrix{ r_Q = \kappa & r_S = \kappa-c_H-c_F & r_W = \kappa-( 2-\gamma) c_H-c_F }$$for some κ ∈ [(2 − γ) c H + c F, 1].
In this case, the best induced equilibrium has a positive probability of both initiation followed by backing down and initiation followed by war: $0< \underline {p}< \overline {p}( x) < 1$
 .
.(ii) Suppose 2c H + c F > 1 − y. Then a retention strategy is optimal if and only if it is of the form
$$\matrix{ r_Q = \kappa & r_S = \kappa-{1\over 2}( 1-y + c_F) & r_W = \kappa-( 1-y-\gamma c_H) }$$for some $\kappa \in [ \max \left \langle {1\over 2}( 1-y + c_F) ,\; \, 1-y-\gamma c_H\right \rangle ,\; \, 1]$
 .
.
In this case, the best induced equilibrium has positive probability of initiation followed by backing down, but probability zero of initiation followed by war: $0< \underline {p}< \overline {p}( x) = 1$
 .
.
The proof that these are the optimal schemes is somewhat involved, so we defer the details to Appendix B. We focus here on the interpretation. To help elucidate the implications of the optimal strategy, we present the salient implications of the characterization as a series of facts.
First, we highlight the behavior that is induced by the optimal strategy. These facts show how the indirect equilibrium effects create incentives to reward and punish leaders who need not represent the citizen's preference over individual crisis outcomes.
FACT 1: The optimal strategy always induces positive probability of initiating a crisis and of backing down.
Every optimal strategy generates crises with positive probability. Importantly, the probability that the crisis results in a war varies with the underlying parameters. This fact speaks directly to the concern found in the audience cost literature noted by Gowa (Reference Gowa1999) and Schultz (Reference Schultz2001b). Citizens benefit when their leaders “bluff” strategically by initiating crises that end peacefully, but this may or may not require rewarding settling more than fighting.
FACT 2: The optimal strategy induces war with positive probability if and only if the total cost of war is low enough (2c H + c F < (1 − y)).
War is possible only when total costs are low. This is quite intuitive. Recall that war is avoided with probability 1 only when the appeasement offer is so high that all types of Home accept. Since the optimal offer is,
we see that increasing F's cost raises the offer (ignoring the cap), while increasing H's cost lowers the cap. Both changes tend to make the cap binding.
The possibility of war in the optimal incentive strategy casts doubt on the classical liberal argument that, if the citizens of a country were in control, the country would be peaceful because it is the citizens who pay the “price of war in blood and money” (Russet, Reference Russet1993, p.30).Footnote 8 Optimal control by the citizens does not eliminate risky behavior. Optimal retention schemes respond to the risk-reward trade off common in unitary actor models of crisis and war.
Interestingly, the decision to use a strategy with positive probability of war is independent of the preference divergence between the leader and the citizen, i.e., if 2c H + c F is greater or less than 1 − y. The form of the optimal strategy, on the other hand, does depend on the preference divergence. This is because the optimal strategy uses the reward for settlement to get the degree of political bias that is optimal for manipulating the offer. How much of that optimal level of political bias needs to come from the reward strategy obviously depends on how much political bias is inherent in the preference divergence.
The form of the optimal retention strategy depends on what kind of behavior the citizen benefits from inducing.
From Proposition 1, we have r S − r W < 0 if and only if 1 − y < 2γc H + c F. Thus:
FACT 3: The optimal strategy punishes backing down relative to fighting if and only if the total costs of war are high enough.
That is, Feaon–Schultz style audience costs, r S − r W < 0, are only optimal when the total costs of war are high and war does not happen. Fact 3 is illustrated in Figure 3.
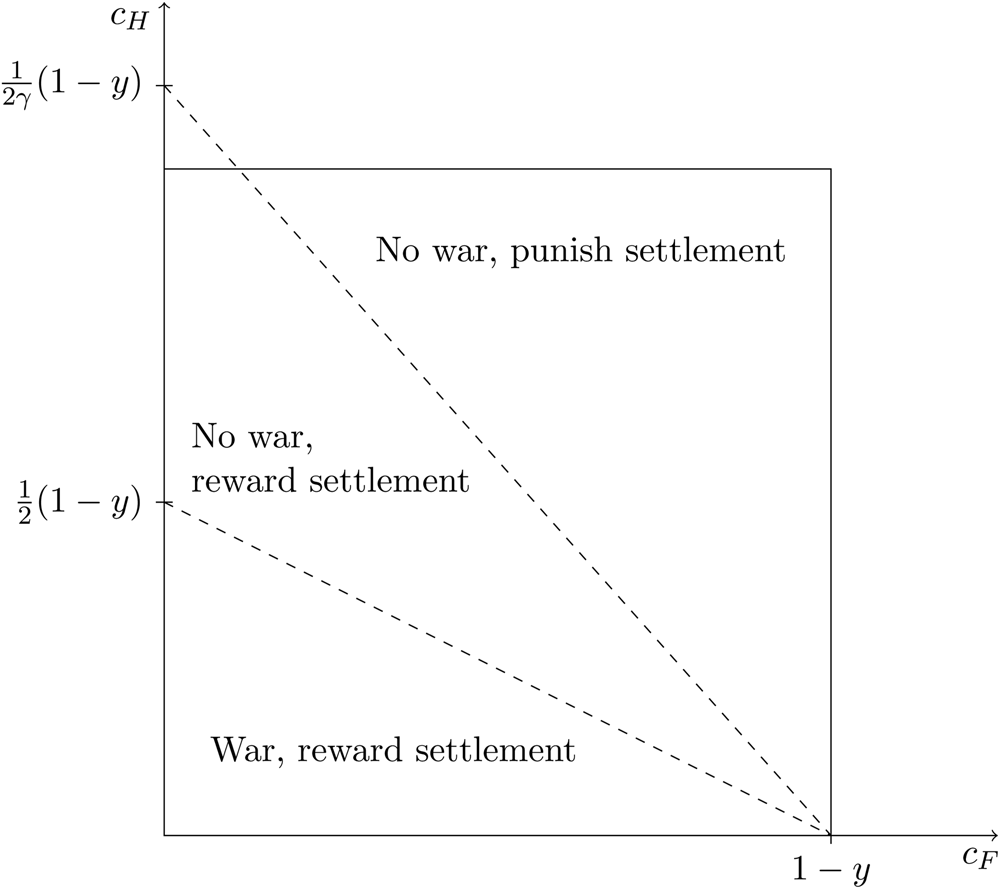
Fig. 3. Characteristics of the equilibrium with the optimal retention strategy, as a function of the costs of fighting. The box delimits the set of costs consistent with the assumption that c H ≤ 1 − y and c F ≤ 1 − y.
In this Fearon-Schultz audience cost case, the citizen benefits from certain settlement at the highest possible level. To secure this, backing down needs to be punished just enough to offset the leader's cost of fighting. Here the incentives work in a manner reminiscent of the intuitions of Fearon (Reference Fearon1994a) and Schultz (Reference Schultz2001b): they make backing down costly, stiffen the leader's stance in bargaining, and lead to a bigger share of the pie. In fact, the optimal audience costs exactly offset the leader's cost of fighting, and Home gets everything when it initiates a crisis.
In the case with positive probability of war, on the other hand, the leader will choose to fight with positive probability. And the set of offers he rejects does not affect the offer that is actually made. Thus, the citizen benefits from offsetting the existing political bias by rewarding backing down relative to fighting. After the crisis has begun, the citizen wants the leader to internalize fully the cost of war. For γ < 1, this means making war less attractive than a settlement.
Whether backing down is rewarded relative to fighting depends on the underlying parameters. By contrast, r Q and r S are unambiguously ordered:
FACT 4: The optimal strategy always punishes backing down relative to the status quo.
Whatever offer the strategy is trying to extract from F, initiation must be limited to improve the offer. But better offers make initiating a crisis more attractive, and retention incentives are always important here. When the probability of war in equilibrium is zero, this is obvious: the offer is an increasing function of the least type who enters. The argument when there is a positive probability of war in equilibrium is a bit more subtle, but just as intuitive: if F is making a very generous offer, then weak types will want to initiate a crisis to take advantage of it. But if F expects that reaction, it will no longer be willing to make the generous offer. Thus, offers can be generous in equilibrium only if accepting those generous offers is costly to leaders. This is a kind of commitment problem face by the leader of Home that the citizen has a strong incentive to address by punishing backing down relative to the status quo. This robust feature of optimal schemes is the one for which Tomz (Reference Tomz2007) finds support in his survey experiments on audience costs.
Finally, the model's comparative statics shed light on when Fearon–Schultz audience costs, i.e. those where backing down leads to a lower probability of retention than fighting, are a good incentive strategy for citizens to use.
FACT 5: As Home's status quo share increases, the audience cost regime (i.e., choosing r S − r W < 0) becomes more likely, in the sense that more combinations of c H and c F make the audience cost regime optimal.
Fact 5 implies we should see empirical evidence of Fearon–Schultz type audience costs, where backing down (settling) is punished electorally compared to fighting, when crises involve countries with very different benefits from the status quo. Examples might be post-Cold War crises involving the US. This fact might also explain the apparent lack of audience costs in the Suez crisis, as the status quo was very unfavorable to the challengers, or in the Cuban Missile Crisis, with the Soviet weapons already on the island, as argued in the evaluation of that case by Snyder and Borghard (Reference Snyder and Borghard2011).
The model also allows us to think about the relationship between incentivizing leaders, through mechanisms like audience costs, and the citizen's foreign policy preferences. Snyder and Borghard (Reference Snyder and Borghard2011) argue that voters’ reaction to a leader's foreign policy is really about policy preferences, not policy consistency, and thus audience costs are not real. For example, they argue that a dovish electorate is more likely to reward peaceful outcomes and a hawkish electorate is more likely to reward demonstrations of strength and resolve. On the first point we agree, in our approach the retention strategy is completely driven by a policy-based desire to managing the principal-agent problem faced by citizens.
How might we think about hawkish or dovish citizen preferences in our model? One possible answer is that a citizenry is hawkish if they preferred to start a crisis, given the conditions facing Home and Foreign, their initial beliefs about the probability of victory, and their expectations about how their leader and the foreign rival would act in a crisis. Alternatively, a citizenry may be dovish if under the same circumstances they prefer the status quo. In terms of our model, a citizenry is hawkish if and only if ${1\over 2} ( 1 + c_F) -c_H( 1-c_F) > y$![]() . Therefore, a citizen prefers their leader to initiate a crisis given their information if the Foreign's war costs are high, Home's costs are low, and the status quo is bad for Home.
. Therefore, a citizen prefers their leader to initiate a crisis given their information if the Foreign's war costs are high, Home's costs are low, and the status quo is bad for Home.
Comparing this condition to those in Proposition 1, and it is easy to see that all combinations of retention regimes and policy preferences can be seen together in cases. Sometimes hawkish citizens should reward peace and backing down. Sometimes dovish citizens should punish settlement and reward war. The citizenry's policy preferences over initiating a crisis and how they should optimally use their political support to incentivize their leader in foreign policy are two separate and largely unrelated issues.
4. Public settlements
The previous section characterized the optimal retention strategy when the details of settlements are secret or citizens are otherwise unable to condition on those details. But it is also of interest to characterize optimal incentives when such details are public.
When settlements are public, a retention strategy no longer specifies a single number r S for the probability of retention in the event of a settlement. Instead, it specifies a function r S : [0, 1] → [0, 1], where r S(x) is the probability of retention when the settlement is x.
We will restrict attention to cutoff reward schemes—functions of the form
for some $\overline {x} \in [ 0,\; \, 1]$![]() and $\underline {r},\; \, \overline {r}\in [ 0,\; \, 1]$
and $\underline {r},\; \, \overline {r}\in [ 0,\; \, 1]$![]() with $\underline {r}\leq \overline {r}$
with $\underline {r}\leq \overline {r}$![]() .
.
The apparent restrictiveness of this family of retention strategies will not turn out to limit what the Home citizen can achieve. Indeed, we will show that the Home citizen can use such a strategy to drive Foreign all the way to indifference between settling and fighting, even though Foreign has all the bargaining power.
4.1 What payoffs are possible?
In any equilibrium, an interval of types [p, 1] will initiate a crisis, while the complementary interval [0, p) will keep the status quo. The search for the best possible equilibrium payoff for the Home citizen can be carried out in two steps, one that asks what can be attained given p, and a second that asks which p is best, given the first answer.
Suppose that Foreign believes that H initiates a crisis if and only if p ≥ μ. If F follows the strategy Fight, it gets payoff ${\cal W}_F$![]() , where
, where

where the second equality uses the uniform distribution of p.
Since this strategy is feasible, F's payoff in any equilibrium must be at least ${\cal W}_F( \underline {p})$![]() . And since the maximal total surplus is 1, the Home citizen's payoff from a continuation equilibrium after all types p ≥ p have initiated is at most ${\cal I}$
. And since the maximal total surplus is 1, the Home citizen's payoff from a continuation equilibrium after all types p ≥ p have initiated is at most ${\cal I}$![]() , where
, where
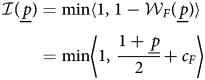
Call a pair (r S, r W) fully extractive at p if, given (r S, r W), equilibrium play in the continuation game gives H payoff ${\cal I}( \underline {p})$![]() . Because war is costly, Foreign's best response to a fully extractive pair must be to offer $x^{{\dagger} } = {\cal I}( \underline {p})$
. Because war is costly, Foreign's best response to a fully extractive pair must be to offer $x^{{\dagger} } = {\cal I}( \underline {p})$![]() .
.
Clearly, the best payoff that the Home citizen can hope for in an equilibrium with initiation cutoff p is $\underline {p} y + ( 1-\underline {p}) {\cal I}( \underline {p})$![]() . And the best possible payoff any equilibrium could give is
. And the best possible payoff any equilibrium could give is
Call a retention strategy maximally extractive if it induces an equilibrium in which the Home citizen's payoff attains the maximum in Program 4.
4.2 How to extract the surplus
As in the case of secret settlements, a key step is to find out which types accept a given offer.
Type p is willing to accept offer x if and only if x + r S(x) ≥ p − γc H + r W. For a cutoff retention scheme, there are two cases. For the cutoff $\overline {x}$![]() , if $x < \overline {x}$
, if $x < \overline {x}$![]() , then the offer is accepted by types p ≤ x + γc H − r W + r. If $x \geq \overline {x}$
, then the offer is accepted by types p ≤ x + γc H − r W + r. If $x \geq \overline {x}$![]() , then the offer is accepted by types $p \leq x + \gamma c_H - r_W + \overline {r}$
, then the offer is accepted by types $p \leq x + \gamma c_H - r_W + \overline {r}$![]() .
.
Again, write the acceptance strategy as a critical type, $\overline {p}( x)$![]() such that types $p\leq \overline {p}( x)$
such that types $p\leq \overline {p}( x)$![]() accept and types $p> \overline {p}( x)$
accept and types $p> \overline {p}( x)$![]() reject. This will be easier to write with the function $\iota _{\underline {p}}$
reject. This will be easier to write with the function $\iota _{\underline {p}}$![]() given by
given by
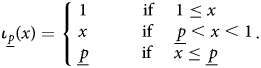
Now we can write the equilibrium acceptance strategy:
Lemma 4 Fix a cutoff reward scheme (r S, r W). In any equilibrium in which the Home leader initiates a crisis if and only if p ≥ p, the Home leader's acceptance strategy is given by:
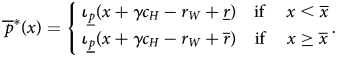
Figure 4 shows that, if $\overline {r} > \underline {r}$![]() , there is a discrete jump in the critical type at $\overline {x}$
, there is a discrete jump in the critical type at $\overline {x}$![]() . Moreover, by taking $\overline {r} - \underline {r} \geq 1 - \underline {p}$
. Moreover, by taking $\overline {r} - \underline {r} \geq 1 - \underline {p}$![]() , that jump can be made to cover the entire range of possible types. This makes it easy to get full extraction.
, that jump can be made to cover the entire range of possible types. This makes it easy to get full extraction.
EXAMPLE 1: Let $x^{{\dagger} } = \min \langle 1,\; \, 1-{\cal W}_F( \underline {p}) \rangle$![]() , and suppose $\underline {p} \leq x^{{\dagger} } + \gamma c_H \leq 1$
, and suppose $\underline {p} \leq x^{{\dagger} } + \gamma c_H \leq 1$![]() . Set $\overline {r} = 1$
. Set $\overline {r} = 1$![]() , r = p, and $r_W = x^{{\dagger} } + \gamma c_H$
, r = p, and $r_W = x^{{\dagger} } + \gamma c_H$![]() . The equilibrium acceptance strategy simplifies to:
. The equilibrium acceptance strategy simplifies to:
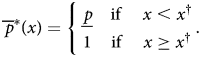
That is, any relevant type is willing to accept an offer of all of the conditional surplus, and none is willing to accept anything less. Clearly, Foreign will offer $x^{{\dagger} }$![]() , and it will be accepted.
, and it will be accepted.
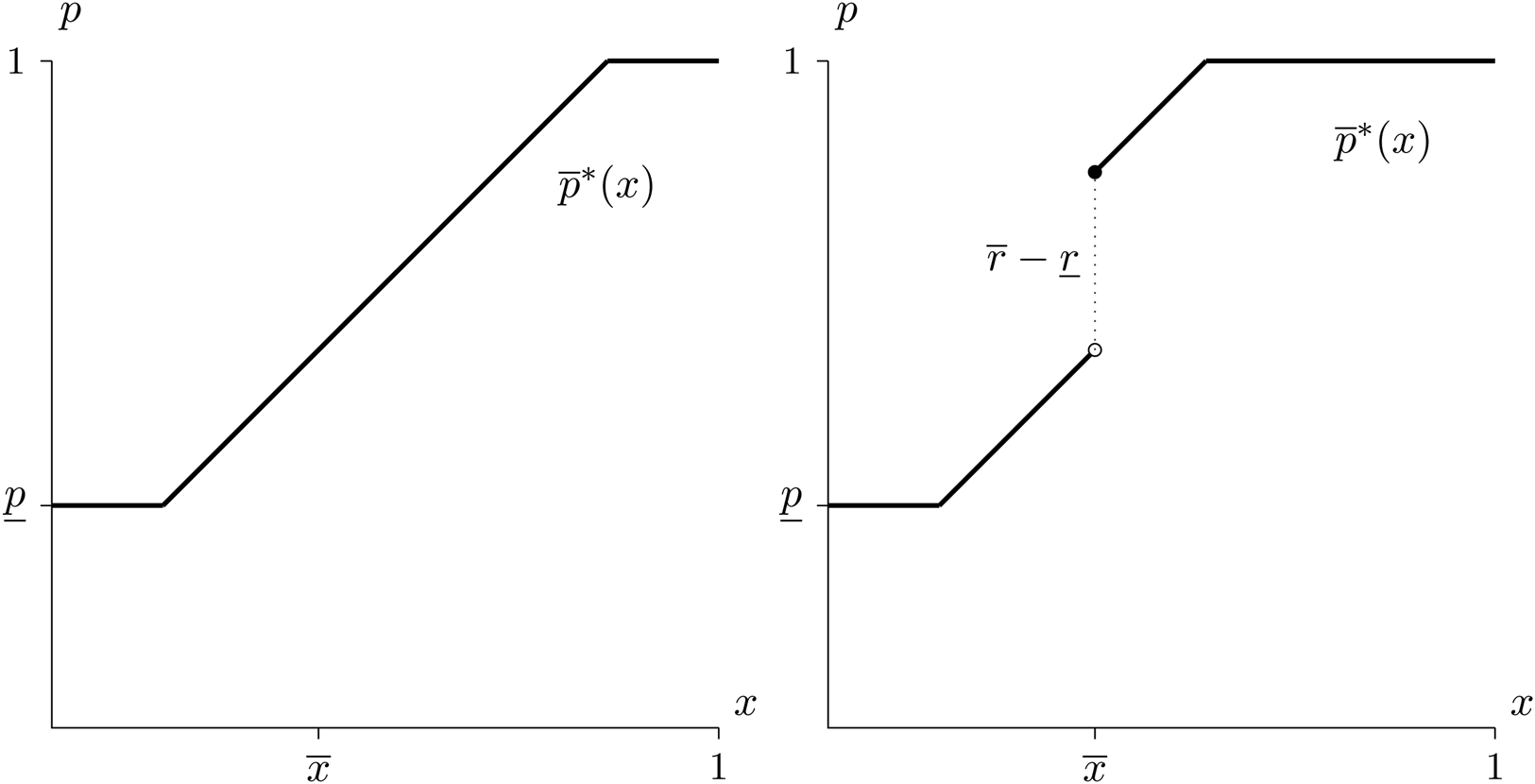
Fig. 4. Each panel shows the Home leader's acceptance function, $\overline {p}$![]() , for a cutoff retention strategy with $\overline {x}$
, for a cutoff retention strategy with $\overline {x}$![]() . The panel on the left has $\underline {r} = \overline {r} = 0$
. The panel on the left has $\underline {r} = \overline {r} = 0$![]() . The panel on the right has $\overline {r} > \underline {r} = 0$
. The panel on the right has $\overline {r} > \underline {r} = 0$![]() .
.
While the argument is not always as simple as the one just given, it turns out that the Home citizen can always fully extract at p.
Proposition 2 Fix p. There is a pair (r S, r W) that is fully extractive at p.
The proof of Proposition 2 is constructive—for any values of the parameters and p, we present a concrete pair (r S, r W) that is fully extractive. In those constructions, we have r = 0 < r W. Substantively, this says that the Home leader would be punished for settlement, relative to war, were he to settle for less than $x^{{\dagger} }$![]() . Importantly, this punishment is off the path, and would not be observable by a researcher studying outcomes of this game empirically.
. Importantly, this punishment is off the path, and would not be observable by a researcher studying outcomes of this game empirically.
While the proof of Proposition 2 uses a pair with off-the-path punishments, it leaves open whether such punishments are necessary for full extraction. The next result shows that they are, at least in our class of cutoff reward schemes. (Notice, Example 1 has such off-path punishments but does not use r = 0.)
Proposition 3: Fix p and let the cutoff reward scheme (r S, r W) be a fully extractive pair. Then r W > r.
4.3 The full optimum
Proposition 2 shows that Home can fully extract the available surplus conditional on (equilibrium) crisis initiation. But a full discussion of the optimal retention strategy requires attention also be paid to which types initiate a crisis. The following example shows that keeping p > 0 can strictly increase the Home citizen's ex ante expected payoff, even when Home's status quo share is lower than the fully extractive offer that would be made conditional on p = 0.
Example 2: Suppose $c_F = {1\over 3}$![]() and $y = {1\over 2}$
and $y = {1\over 2}$![]() . If all types of Home initiate a crisis, then the Home citizen's ex ante expected payoff is $1 - ( {\opf E}( 1 - p) - c_F) = {5\over 6}$
. If all types of Home initiate a crisis, then the Home citizen's ex ante expected payoff is $1 - ( {\opf E}( 1 - p) - c_F) = {5\over 6}$![]() . If Home initiates a crisis if and only if $p > {1\over 6}$
. If Home initiates a crisis if and only if $p > {1\over 6}$![]() , then the fully-extractive offer is
, then the fully-extractive offer is
Thus the ex ante expected payoff to the Home citizen is
Example 2 illustrates the importance of being able to extend a fully extractive retention scheme to a complete retention strategy that creates the appropriate incentives for crisis initiation. Not all fully extractive retention schemes can be so extended.
Example 3 (Example 1, continued): Suppose $0 < \underline {p} \leq x^{{\dagger} } + \gamma c_H \leq 1$![]() , and $y < x^{{\dagger} }$
, and $y < x^{{\dagger} }$![]() . Consider the fully extractive scheme given by $\overline {r} = 1$
. Consider the fully extractive scheme given by $\overline {r} = 1$![]() , r = p, and $r_W = x^{{\dagger} } + \gamma c_H$
, r = p, and $r_W = x^{{\dagger} } + \gamma c_H$![]() . To extend this to a full retention strategy that gives types p < p an incentive to keep the status quo, we must have $y + r_S = x^{{\dagger} } + 1$
. To extend this to a full retention strategy that gives types p < p an incentive to keep the status quo, we must have $y + r_S = x^{{\dagger} } + 1$![]() , or
, or
But this is not feasible, since r S cannot exceed 1.
Example 3 shows that it is too much to hope for that every fully-extractive scheme can be extended to a complete retention strategy, that is one that also considered crisis initiation incentives. Fix some parameters y and c F, and let p be the maximizer from Program 4. Proposition 2 shows that there are retention schemes that are fully extractive in the continuation equilibrium following crisis initiation by types p ≥ p. The next result shows that at least one of these fully-extractive schemes can, in fact, be extended to a complete retention strategy that is maximally extractive.
Proposition 4 Fix c F and y. There is a maximally extractive retention strategy. That strategy induces all types to initiate a crisis if and only if $y \leq c_F \leq {1\over 2}$![]() .
.
Since citizens can condition on the settlement or not in the public settlements case, citizens do better when settlements are public than when they are secret. Figure 5 gives more detail on how the optimal retention strategy varies as a function of c F and y. The triangle is the set of (c F, y) pairs that are consistent with the assumption that c F ≤ 1 − y. Each of the four regions is labeled according to whether all types initiate a crisis or not, and whether the offer is equal to 1. Observe that an offer equal to 1 implies that initiation is limited, but the converse does not hold.
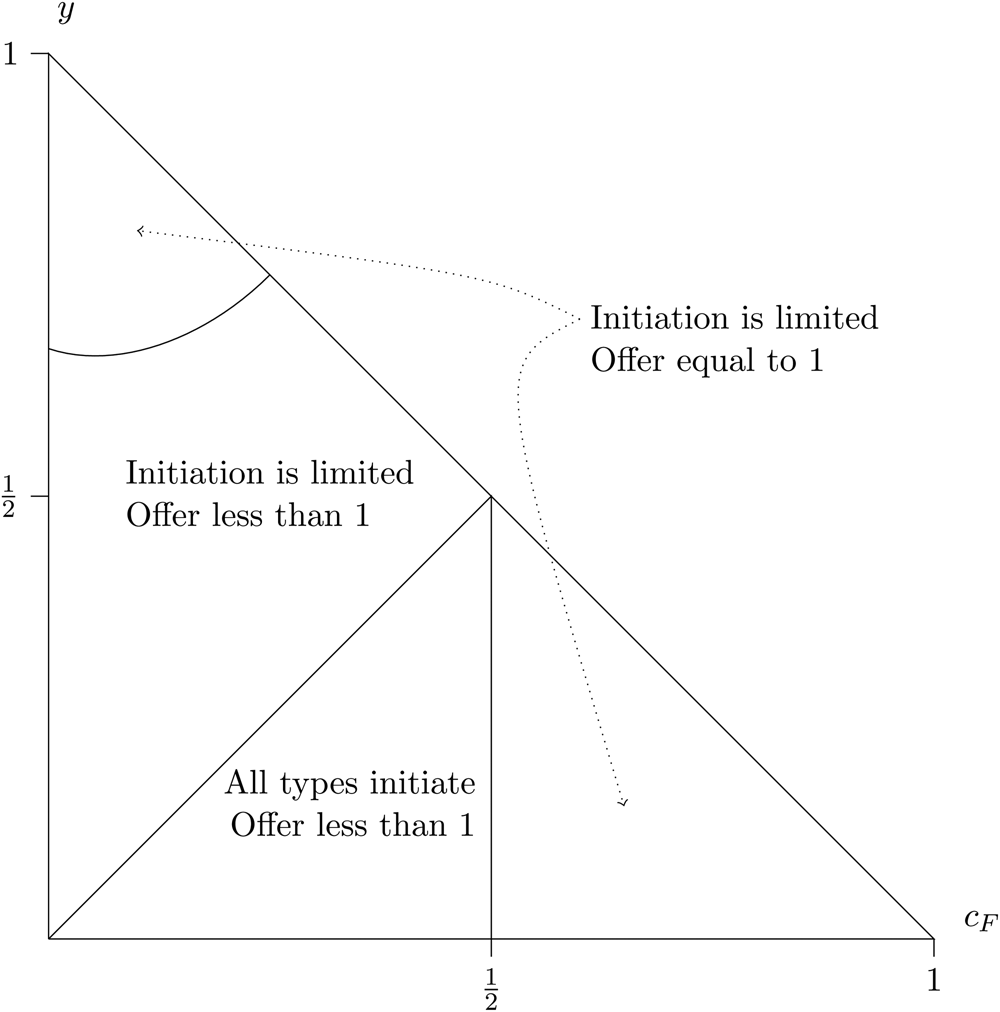
Fig. 5. The form of maximally extractive retention strategies as a function of c F and y.
The preceding analysis means that if the citizen can condition their retention on the details of the settlement, then they can fully extract the surplus from the international bargain, and occasionally the entire pie. The additional wrinkle is that because this fully extractive offer is set by Foreign as a function of the types of Home that choose to initiate crises, there is a trade-off between inducing more leader types initiating crises and getting access to offers and the size of the offer. This means that there is an interior optimum where not all types initiate; which turns out to always be supportable in equilibrium with appropriate retention incentives, despite the risk that high offers might induce low types to want to initiate crises.
Furthermore, with public settlements, there is no war and no agency loss. In fact, delegation and optimal retention allows the citizen to achieve outcomes they could not if they were playing the game themselves. Like before, such a retention plan does not represent in any meaningful way the citizen's preferences over outcomes of war and peace directly, only indirectly through their effects in equilibrium play of the crisis game.
5. Conclusion
We have characterized the optimal incentive strategy for a citizen to give to a ruler who might engage in a simple form of crisis bargaining, allowing us to endogenize the domestic political constraints. These political constraints are sensitive to two different agency problems. The first is the divergence between the leader's private payoff to war and the citizens’ payoffs to war. The second is a commitment problem faced by the leader. This commitment problem comes from the fact that committing to keep the status quo unless the private information received by the leaders is quite favorable for Home's prospects in war leads to high appeasement offers in the case of initiation, but those same high offers make it attractive to initiate a crisis when their signal is not so favorable.
The optimal response to the commitment problem is quite robust: the leader should always face a lower probability of retention after backing down than if she keeps the status quo. This allows a citizen to manage the leader's commitment problem. But the incentive related to the decision to enhance or offset the leader's political bias is more sensitive to the environment. When total costs of war are low, the optimal scheme offsets the leader's political bias by rewarding backing down more than going to war. This leads the leader to fully internalize the costs of fighting, an action she nonetheless takes with positive probability in the equilibrium. When total costs of fighting are large, on the other hand, the optimal scheme leads to peace with probability one. In this case, the citizen enhances the bargaining power of the leader by punishing her for backing down rather than fighting. For example, if there is a real risk of war, one will not see punishment for backing down relative to fighting, but you will always see electoral costs relative to the status quo.
While the model is too stylized to capture the full richness of empirical discussions of audience costs, it does help clear up an ambiguity in the literature's treatment of the issue. In Fearon (Reference Fearon1994a) canonical theoretical discussion, as well as in the cases discussed by Schultz (Reference Schultz2001b), audience costs refer to punishment for backing down once a crisis has started. Another take on audience costs, one tested in Tomz's Reference Tomz2007 survey experiments, is that they are costs associated with initiating and then backing down. In terms of our model, Fearon and Schultz are discussing the contrast between retention probabilities conditional on backing down and on war, while Tomz is talking about the contrast between retention probabilities conditional on backing down and on keeping the status quo from the beginning. The model highlights that these are conceptually different parts of the optimal incentive strategy, and that whether each is used responds to different aspects of the agency problem.
The optimal retention strategy for public settlements with fully rational citizens problematizes some empirical literature on punishment and audience costs. With public settlements, Home's leader is thrown out for sure if she accepts any offer, leaving Foreign some surplus. This corresponds to the classical idea of punishment for initiating a crisis and then backing down. The result shows there can be a microfoundation for the standard audience cost argument without implying that punishments are ever observed because they occur only off the equilibrium path.
There is clearly work to be done before we have a full picture of leader and citizens’ incentives for the agency problem during a crisis, but the political agency approach provides both a benchmark for optimal citizen behavior and a clear characterization of the primary incentives driving leader's decision in international crises.
Acknowledgments
We received helpful comments and suggestions from Serra Boranbay, Ethan Bueno de Mesquita, Justin Fox, Joanne Gowa, Navin Kartik, Insong Kim, Tom Romer, Scott Tyson, and seminar audiences at the LSE, Purdue, Stanford, Warwick, Wisconsin, the APSA and SPSA annual meetings, the Columbia Conference on Political Economy, and the Princeton University Conference on Game Theoretic Analysis of Conflict. We also thanks James Mao and Niels Markwat for helpful research assistance.
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1017/psrm.2022.34.
Appendix A: Proofs for Section 2
Proof of Lemma 2. Evaluating the integral shows that Q is quadratic with the coefficient on x 2 is $-{1\over 2( 1-\underline {p}) }$![]() , so Q is concave. Since the other two components of U are linear, this shows that U is strictly concave on (p − (r S − r W) − γc H, ∞) and constant otherwise, so it is globally quasiconcave. Furthermore, U is continuous and is differentiable except possibly at x = p − (r S − r W) − γc H.
, so Q is concave. Since the other two components of U are linear, this shows that U is strictly concave on (p − (r S − r W) − γc H, ∞) and constant otherwise, so it is globally quasiconcave. Furthermore, U is continuous and is differentiable except possibly at x = p − (r S − r W) − γc H.
The next step is to look more closely at Q as a function on all of ${\opf R}$![]() . Multiply through by (1 − p) and differentiate (remembering that $\overline {p}'( x) = 1$
. Multiply through by (1 − p) and differentiate (remembering that $\overline {p}'( x) = 1$![]() ) to get
) to get
Equate this to 0 and solve to see that Q is maximized at x = p + c F.
This means that U is nondecreasing up to
and is strictly decreasing thereafter. Thus x* is always an optimal offer. If x* > p − (r S − r W) − γc H, then x* is the unique optimizer. If x* ≤ p − (r S − r W) − γc H, on the other hand, then any x ≤ p − (r S − r W) − γc H is optimal. □
Appendix B: Proofs for Section 3
B.1 Proof of Proposition 1
We will consider two optimization problems. First, the equilibrium problem (EP) is to maximize the citizen's ex ante payoff subject to the constraints that
(i) the retention rule is feasible: r ∈ [0, 1] 3,
(ii) the strategies are feasible: p ∈ [0, 1], x ∈ [0, 1], and $\overline {p}( x) \in [ 0,\; \, 1]$
 for all x ∈ [0, 1], and
for all x ∈ [0, 1], and(iii) the strategies of H and F are part of an assessment that is a PBE: $( \underline {p},\; \, \overline {p}({\cdot}) ,\; \, x) \in {\cal E}( {\bf r})$
 .
.
Write ${\cal F}$![]() for the set of $( {\bf r},\; \, \underline {p},\; \, \overline {p}({\cdot}) ,\; \, x)$
for the set of $( {\bf r},\; \, \underline {p},\; \, \overline {p}({\cdot}) ,\; \, x)$![]() satisfying the first two sets of constraints.
satisfying the first two sets of constraints.
Then, by Lemmas 1–3, we can formally define EP asFootnote 9 :

Let ${\cal V}^{EP}$![]() be the value of EP.
be the value of EP.
Rather than attack the EP directly, we will consider a simpler problem, and show that solutions to the simpler problem allow us to construct solutions to EP. Let Δ = r S − r W, and let
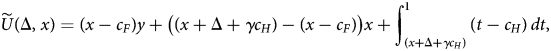
and define the relaxed problem (RP) as:
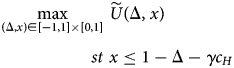
Let ${\cal V}^{RP}$![]() be the value of the relaxed problem.
be the value of the relaxed problem.
LEMMA 5: The value of RP is an upper bound on the value of EP: ${\cal V}^{RP}\geq {\cal V}^{EP}$![]() .
.
Proof.
(i) Start by considering the intermediate program:
$$\eqalign{\max_{( \Delta, \underline{\,p}, \hat{\,p}, x) \in [ -1, 1] \times [ 0, 1] ^{3}} & \ U( \underline{\,p},\; \hat{\,p},\; x) \cr \operatorname{st} & \ \hat{\,p} = x + \Delta + \gamma c_H \cr & \ x\leq \underline{\,p} + c_F\cr & \ x\leq 1-\Delta-\gamma c_H.}$$Inspection of the constraints in EP and this intermediate program shows that the intermediate program has weakly greater value. (Notice that the constraint x ≤ 1 − Δ − γc H ensures that $\hat {p}$
 is less than or equal to 1.)
is less than or equal to 1.)(ii) At any solution to the intermediate program, the constraint x ≤ p + c F must bind.
The solution neglecting both inequality constraints is to set x = 1, p = 0, and Δ = −γc H. But that violates the first inequality constraint.
Now assume the second inequality constraint binds. The offer is then x = 1 − Δ − γc H. Given that, the equality constraint implies $\hat {p} = 1$
 , and the payoff is$$\underline{\,p}y + ( 1-\underline{\,p}) x.$$If the first inequality constraint does not bind, then the solution must be for x = 1 and p = 0. But then p + c F = c F < 1 = x, contradicting the claim that the first constraint is slack.
, and the payoff is$$\underline{\,p}y + ( 1-\underline{\,p}) x.$$If the first inequality constraint does not bind, then the solution must be for x = 1 and p = 0. But then p + c F = c F < 1 = x, contradicting the claim that the first constraint is slack.
(iii) Substitute $\hat {p} = x + \Delta + \gamma c_H$
 and x = p + c F into U to get $\widetilde {U}$
and x = p + c F into U to get $\widetilde {U}$ .
.(iv) Thus, RP has the same value as the intermediate program. □
Lemma 6:
(i) Fix y, c H, and c F. RP has a unique solution.
(ii) Suppose 2c H + c F ≤ 1 − y. Then the solution to RP is
$$( \Delta^{\ast },\; x^{\ast }) = \left(( 1-\gamma) c_H,\; y + c_H + c_F\right).$$
(iii) Suppose 2c H + c F > 1 − y. Then the solution to RP is
$$( \Delta^{\ast },\; x^{\ast }) = \left({1\over 2}( 1-y-c_F) -\gamma c_H,\; {1\over 2}( 1 + y + c_F) \right).$$
Proof.
(i) The second derivative of $\widetilde {U}$
 is$${\bf D}^{2} \widetilde{U} ( \Delta,\; x) = \left(\matrix{-1 & 0 \cr 0 & -1 }\right),\;$$so $\widetilde {U}$
is$${\bf D}^{2} \widetilde{U} ( \Delta,\; x) = \left(\matrix{-1 & 0 \cr 0 & -1 }\right),\;$$so $\widetilde {U}$
 is strictly concave.
is strictly concave.(ii) The unconstrained maximizer of $\widetilde {U}$
 solves the first-order conditions for Δ and x, respectively:$$\eqalign{x - x - \Delta - \gamma c_H + c_H & = 0 \cr y + ( \Delta + \gamma c_H + c_F) - x - \Delta - \gamma c_H + c_H & = 0 .}$$solve these to get
solves the first-order conditions for Δ and x, respectively:$$\eqalign{x - x - \Delta - \gamma c_H + c_H & = 0 \cr y + ( \Delta + \gamma c_H + c_F) - x - \Delta - \gamma c_H + c_H & = 0 .}$$solve these to get $$( \Delta^{\ast },\; x^{\ast }) = \left(( 1 - \gamma) c_H ,\; y + c_H + c_F \right).$$This is consistent with the constraint just if x* ≤ 1 − Δ* − γc H, or
$$( \Delta^{\ast },\; x^{\ast }) = \left(( 1 - \gamma) c_H ,\; y + c_H + c_F \right).$$This is consistent with the constraint just if x* ≤ 1 − Δ* − γc H, or (B.1)$$2c_H + c_F\leq 1-y.$$
(B.1)$$2c_H + c_F\leq 1-y.$$
All that can go wrong is that x might not be interior. This will happen if x ≥ 1, or
$$y + c_H + c_F\geq 1.$$But this is inconsistent with Inequality B.1.
(iii) For 2c H + c F > 1 − y, the unconstrained maximizer violates the constraint. This implies the constraint binds, and we can substitute the constraint into the objective to get
(B.2)$$\max_{x \in [ 0, 1] } ( x - c_F) y + ( 1 - x + c_F) x.$$
Ignoring the boundary constraints on x, the unique maximizer is $x^{\ast } = {1\over 2}( 1 + y + c_F)$
 . This is consistent with the boundary constraint if and only if x* ≤ 1, or$$c_F \leq 1 - y$$which, is an assumption of the model.
. This is consistent with the boundary constraint if and only if x* ≤ 1, or$$c_F \leq 1 - y$$which, is an assumption of the model.
We can then back out Δ* from the constraint to get
$$( \Delta^{\ast },\; x^{\ast }) = \left({1\over 2} - {1\over 2} y - {1\over 2} c_F - \gamma c_H,\; {1\over 2}( 1 + y + c_F) \right).\quad\quad\quad\quad\squ$$
Lemma 7 Suppose (Δ*, x*) is a solution to RP. Then, for the retention strategy,
there exists p* and $\overline {p}^{\ast }({\cdot})$![]() such that $( \underline {p}^{\ast },\; \, \overline {p}^{\ast }({\cdot}) ,\; \, x^{\ast }) \in {\cal E}( {\bf r^{\ast }})$
such that $( \underline {p}^{\ast },\; \, \overline {p}^{\ast }({\cdot}) ,\; \, x^{\ast }) \in {\cal E}( {\bf r^{\ast }})$![]() and that profile gives the citizen payoff $\widetilde {U}( \Delta ,\; \, x)$
and that profile gives the citizen payoff $\widetilde {U}( \Delta ,\; \, x)$![]() .
.
Proof. We proceed by cases, one for each of the two statements in Lemma 6.
(i) Suppose 2c H + c F < 1 − y.
From Lemmas 1 and 6, the Home leader's acceptance strategy is given by
$$\eqalign{\overline{\,p}^{\ast }( x^{\ast }) & = \min\langle 1,\; y + 2c_H + c_F\rangle \cr & = y + 2c_H + c_F \cr & \leq 1.}$$
Lemma 3 and the definition of r* imply that any $\underline {p}< \overline {p}^{\ast }( x^{\ast })$
 is a best response for the Home leader. Choose $\underline {p}^{\ast } = y + c_H< y + 2c_H + c_F = \overline {p}^{\ast }( x^{\ast })$
is a best response for the Home leader. Choose $\underline {p}^{\ast } = y + c_H< y + 2c_H + c_F = \overline {p}^{\ast }( x^{\ast })$ . Then min〈p* + c F, 1 − c H〉 = 1 + c H + c F = x*, and Lemma 2 tells us that x* is a best response for Foreign.
. Then min〈p* + c F, 1 − c H〉 = 1 + c H + c F = x*, and Lemma 2 tells us that x* is a best response for Foreign.The Home Citizen's payoff is
$$\eqalign{& \underline{\,p}^{\ast }y + \left(\overline{\,p}^{\ast }( x^{\ast }) -\underline{\,p}^{\ast }\right)x^{\ast } + \int_{\overline{\,p}^{\ast }( x^{\ast }) }^{1} ( t-c_H) \, dt \cr & \quad = ( y + c_H) y + ( x^{\ast } + \Delta^{\ast } + \gamma c_H-y-c_H) x^{\ast } + \int_{y + 2c_H + c_F}^{1} ( t-c_H) \, dt \cr & \quad = ( x^{\ast }-c_F) + ( \Delta^{\ast } + \gamma c_H + c_F) x^{\ast } + \int_{x^{\ast } + \Delta^{\ast } + \gamma c_H}^{1} ( t-c_H) \, dt \cr & \quad = \widetilde{U}( \Delta^{\ast },\; x^{\ast }) ,\; }$$where the second equality uses the definitions of Δ* and x*.
(ii) Suppose 2c H + c F ≥ 1 − y.
From Lemmas 1 and 6, the Home leader's acceptance strategy is given by $\overline {p}^{\ast }( x^{\ast }) = 1$
 .
.Lemma 3 and the definition of r* imply that any $\underline {p}< \overline {p}^{\ast }( x^{\ast })$
 is a best response for the Home leader. Choose p* = y + c H. Then $\min \langle \underline {p}^{\ast } + c_F,\; \, {1\over 2}( 1 + y + c_F) \rangle = x^{\ast }$
is a best response for the Home leader. Choose p* = y + c H. Then $\min \langle \underline {p}^{\ast } + c_F,\; \, {1\over 2}( 1 + y + c_F) \rangle = x^{\ast }$ , and Lemma 2 tells us that x* is a best response for Foreign.
, and Lemma 2 tells us that x* is a best response for Foreign.Lemma 3 and the definition of r* imply that any $\underline {p}< \overline {p}^{\ast }( x^{\ast })$
 is a best response for the Home leader. Choose $\underline {p}^{\ast } = x^{\ast }-c_F = {1\over 2}( 1 + y-c_F)$
is a best response for the Home leader. Choose $\underline {p}^{\ast } = x^{\ast }-c_F = {1\over 2}( 1 + y-c_F)$ . Then $\min \langle \underline {p}^{\ast } + c_F,\; \, {1\over 2}( 1 + y + c_F) \rangle = x^{\ast }$
. Then $\min \langle \underline {p}^{\ast } + c_F,\; \, {1\over 2}( 1 + y + c_F) \rangle = x^{\ast }$ , and Lemma 2 tells us that x* is a best response for Foreign.
, and Lemma 2 tells us that x* is a best response for Foreign.The Home Citizen's payoff is
$$\eqalign{& \underline{\,p}^{\ast }y + \left(\overline{\,p}^{\ast }( x^{\ast }) -\underline{\,p}^{\ast }\right)x^{\ast } + \int_{\overline{\,p}^{\ast }( x^{\ast }) }^{1} ( t-c_H) \, dt \cr & \quad = ( x^{\ast }-c_F) y + ( 1-x^{\ast } + c_F) x^{\ast } + \int_{1}^{1} ( t-c_H) \, dt \cr & \quad = ( x^{\ast }-c_F) + ( \Delta^{\ast } + \gamma c_H + c_F) x^{\ast } + \int_{x^{\ast } + \Delta^{\ast } + \gamma c_H}^{1} ( t-c_H) \, dt \cr & \quad = \widetilde{U}( \Delta^{\ast },\; x^{\ast }) ,\; }$$where the second equality uses the definitions of Δ* and x*. □
Lemma 8: Suppose r is a retention strategy and $( \underline {p},\; \, \overline {p}({\cdot}) ,\; \, x) \in {\cal E}( {\bf r})$![]() . Then $( \underline {p},\; \, \overline {p}({\cdot}) ,\; \, x)$
. Then $( \underline {p},\; \, \overline {p}({\cdot}) ,\; \, x)$![]() gives the citizen payoff ${\cal V}^{RP}$
gives the citizen payoff ${\cal V}^{RP}$![]() if and only if r Q − r S = x − y and r S − r W = Δ.
if and only if r Q − r S = x − y and r S − r W = Δ.
Proof. Such an r induces either a different Δ or different p, and thus a different x. But $\widetilde {U}$![]() just is the citizen's payoff as a function of Δ and x. □
just is the citizen's payoff as a function of Δ and x. □
Proof of Proposition 1. Lemma 5 gives ${\cal V}^{RP}\geq {\cal V}^{EP}$![]() . Since Lemma 7 gives an equilibrium with payoff ${\cal V}^{RP}$
. Since Lemma 7 gives an equilibrium with payoff ${\cal V}^{RP}$![]() , we have ${\cal V}^{EP}\geq {\cal V}^{RP}$
, we have ${\cal V}^{EP}\geq {\cal V}^{RP}$![]() . Together, these imply ${\cal V}^{EP} = {\cal V}^{RP}$
. Together, these imply ${\cal V}^{EP} = {\cal V}^{RP}$![]() . Lemma 8 then implies that r ∈ [0, 1]3 implements ${\cal V}^{EP}$
. Lemma 8 then implies that r ∈ [0, 1]3 implements ${\cal V}^{EP}$![]() if and only if r Q − r S = x − y and r S − r W = Δ. Substituting the solutions from Lemma 6 gives the form of the optimal r The inequalities involving p and $\overline {p}( x)$
if and only if r Q − r S = x − y and r S − r W = Δ. Substituting the solutions from Lemma 6 gives the form of the optimal r The inequalities involving p and $\overline {p}( x)$![]() are immediate from the constructions in the proof of Lemma 7. □
are immediate from the constructions in the proof of Lemma 7. □
Appendix C: Proofs for Section 4
Proof of Proposition 2. Let $x^{{\dagger} } = \min \left \langle {1 + p\over 2} + c_F,\; \, 1 \right \rangle$![]() , and
, and
We will proceed in two steps. First, we will show that, if the Home leader adopts $\hat {\overline {p}}$![]() as her acceptance strategy, then Foreign best responds by offering $x^{{\dagger} }$
as her acceptance strategy, then Foreign best responds by offering $x^{{\dagger} }$![]() . Second, we construct retention strategies that make $\hat {\overline {p}}$
. Second, we construct retention strategies that make $\hat {\overline {p}}$![]() a best response by the Home leader.
a best response by the Home leader.
Step 1:
Start with two easy observations.
Claim 1: $x \geq x^{{\dagger} }$![]() implies x ≥ c F.
implies x ≥ c F.
Claim 2: Suppose the Home leader uses strategy $\hat {\overline {p}}$![]() . All types accept any offer $x \geq x^{{\dagger} }$
. All types accept any offer $x \geq x^{{\dagger} }$![]() .
.
These set up the main argument.
Claim 3: If $x< x^{{\dagger} }$![]() is a best response to $\hat {\overline {p}}$
is a best response to $\hat {\overline {p}}$![]() , then it must satisfy $x \leq \check {x} = \underline {p} + c_F$
, then it must satisfy $x \leq \check {x} = \underline {p} + c_F$![]() .
.
Proof. For any offer x, F's payoff is

On $( \check {x},\; \, x^{{\dagger} })$![]() , then $\hat {\overline {p}}( x) = x-c_F$
, then $\hat {\overline {p}}( x) = x-c_F$![]() , and $\hat {\overline {p}}'( x) = 1$
, and $\hat {\overline {p}}'( x) = 1$![]() . Thus, on that interval,
. Thus, on that interval,
so no $x \in ( \check {x},\; \, x^{{\dagger} })$![]() can be a best response. □
can be a best response. □
Claim 4 At offer $x\leq \check {x}$![]() , war occurs with probability 1.
, war occurs with probability 1.
Proof. Since $\hat {\overline {p}}$![]() is non-decreasing, the acceptance threshold at $x\leq \check {x}$
is non-decreasing, the acceptance threshold at $x\leq \check {x}$![]() is $\hat {\overline {p}}( x) \leq \hat {\overline {p}}( \check {x}) = \underline {p}$
is $\hat {\overline {p}}( x) \leq \hat {\overline {p}}( \check {x}) = \underline {p}$![]() . □
. □
Claims 3, 4, and the definition of $x^{{\dagger} }$![]() imply that offering $x^{{\dagger} }$
imply that offering $x^{{\dagger} }$![]() is a best response to $\hat {\overline {p}}$
is a best response to $\hat {\overline {p}}$![]() .
.
Step 2: We treat the cases $x^{{\dagger} } = 1$![]() and $x^{{\dagger} } = {1 + p\over 2} + c_F < 1$
and $x^{{\dagger} } = {1 + p\over 2} + c_F < 1$![]() separately.
separately.
(i) Suppose $x^{{\dagger} } = 1$
 , and consider the retention strategy given by:$$\matrix{ \overline{x} = 1 & \overline{r} = c_F & \underline{r} = 0 & r_W = c_F + \gamma c_H }.$$Lemma 4 applied to this strategy yields:
, and consider the retention strategy given by:$$\matrix{ \overline{x} = 1 & \overline{r} = c_F & \underline{r} = 0 & r_W = c_F + \gamma c_H }.$$Lemma 4 applied to this strategy yields: $$\overline{\,p}^{\ast }( x) = \left\{\matrix{ x - c_F & {\rm if }\quad\, x< 1 \cr 1 & {\rm if }\quad\, x = 1 }\right.$$
$$\overline{\,p}^{\ast }( x) = \left\{\matrix{ x - c_F & {\rm if }\quad\, x< 1 \cr 1 & {\rm if }\quad\, x = 1 }\right.$$
(ii) Suppose $x^{{\dagger} } = {1 + p\over 2} + c_F < 1$
 , and consider the retention strategy given by:$$\matrix{ \overline{x} = {1 + p\over 2} + c_F & \overline{r} = {1-\underline{\,p}\over 2} & \underline{r} = 0 & r_W = c_F + \gamma c_H }.$$Lemma 4 applied to this strategy yields:
, and consider the retention strategy given by:$$\matrix{ \overline{x} = {1 + p\over 2} + c_F & \overline{r} = {1-\underline{\,p}\over 2} & \underline{r} = 0 & r_W = c_F + \gamma c_H }.$$Lemma 4 applied to this strategy yields: $$\overline{\,p}^{\ast }( x) = \left\{\matrix{ x - c_F & {\rm if }\quad\, x< 1 \cr 1 & {\rm if }\quad\, x = 1. }\right.\quad \quad \quad \quad \squ $$
$$\overline{\,p}^{\ast }( x) = \left\{\matrix{ x - c_F & {\rm if }\quad\, x< 1 \cr 1 & {\rm if }\quad\, x = 1. }\right.\quad \quad \quad \quad \squ $$
Proof of Proposition 3. Recall that ${\cal W}_F( \underline {p})$![]() is the expected payoff that Foreign gets from fighting all types at least p.
is the expected payoff that Foreign gets from fighting all types at least p.
Since (r S, r W) is a fully-extractive cutoff reward scheme, r S has the form
where $x^{{\dagger} } = 1 - {\cal W}_F( \underline {p})$![]() . Moreover, there is an equilibrium of the continuation game in which $x^{{\dagger} }$
. Moreover, there is an equilibrium of the continuation game in which $x^{{\dagger} }$![]() is offered by Foreign, and is accepted by all types of Home. For $x^{{\dagger} }$
is offered by Foreign, and is accepted by all types of Home. For $x^{{\dagger} }$![]() to be a best response, it must be that any smaller offer would be rejected by a positive measure of types, else Foreign would have a profitable deviation to a smaller off that was also accepted almost surely. And Lemma 4 implies that the Home Leader's acceptance strategy in such a continuation equilibrium is
to be a best response, it must be that any smaller offer would be rejected by a positive measure of types, else Foreign would have a profitable deviation to a smaller off that was also accepted almost surely. And Lemma 4 implies that the Home Leader's acceptance strategy in such a continuation equilibrium is
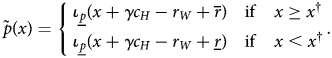
A slight modification of the proof of Lemma 2 implies that Foreign's best response to $\tilde {p}$![]() is either the least offer that is accepted for sure, $x^{{\dagger} }$
is either the least offer that is accepted for sure, $x^{{\dagger} }$![]() , or is $x_{\dagger} = \underline {p} + c_F$
, or is $x_{\dagger} = \underline {p} + c_F$![]() . Thus we need to show that Foreign's payoff from offering $x_{\dagger}$
. Thus we need to show that Foreign's payoff from offering $x_{\dagger}$![]() is not greater than ${\cal W}_F( \underline {p})$
is not greater than ${\cal W}_F( \underline {p})$![]() .
.
Suppose, seeking a contradiction, that there is an ɛ > 0 such that types in [p, p + ɛ) accept the offer $x_{\dagger}$![]() , while types greater than p + ɛ reject it. (If this is not true, then Foreign's payoff from that offer is exactly ${\cal W}_F( \underline {p})$
, while types greater than p + ɛ reject it. (If this is not true, then Foreign's payoff from that offer is exactly ${\cal W}_F( \underline {p})$![]() , by monotonicity of the Home leaders's acceptance strategy.) Then Foreign's payoff to offering $x_{\dagger}$
, by monotonicity of the Home leaders's acceptance strategy.) Then Foreign's payoff to offering $x_{\dagger}$![]() , denoted ${\sf V}$
, denoted ${\sf V}$![]() , is
, is
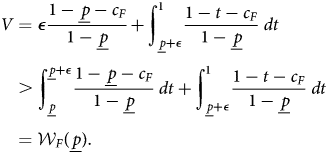
Thus it must be the case that no type accepts $x_{\dagger}$![]() . In particular, the least type, p, must reject it. This requires
. In particular, the least type, p, must reject it. This requires
or
Since γc H + c F > 0, we must have r W > r. □
Proof of Proposition 4 is in the supplementary materials.



















