1 Introduction
Geographically defined legislative districts present a temptation for politically motivated mapmakers. It has long been understood that those responsible for drawing districts may pervert mechanisms of representation by drawing the boundaries of districts in ways that advantage (or disadvantage) certain groups. A recent example illustrates this point. In 2010, Scott Walker won election as governor of Wisconsin. In addition to Walker’s victory, Republicans running for seats in Wisconsin’s State Senate and Assembly benefited from a wave of discontent with Democrats and established majorities in both chambers of Wisconsin’s state legislature. The victory was well timed because following the census in 2010, Walker and legislative Republicans had the opportunity to redraw the state’s state-legislative and congressional districts in advance of the 2012 election without meaningful Democratic opposition. The result was a set of legislative districts that ensured significant Republican majorities in Wisconsin’s legislature and congressional delegation. When a group of Democratic voters challenged the map of state-legislative districts in federal court, an expert testifying on behalf of the Democrats argued that the Republican drawn districts potentially undermined a core principal of representative democracy, majority rule. The expert argued that it would take a “political earthquake” for Democrats to win a majority of seats in the legislature even though Wisconsin Democrats frequently won a majority of votes cast in legislative elections and in state-wide races (Johnson Reference Johnson2016a). Wisconsin Republicans countered that their advantage grew out of the concentration of Democrats in urban areas, and the map they drew simply reflected the more efficient distribution of Republicans in suburban and rural areas (Johnson Reference Johnson2016b). The question left for the panel of federal judges hearing the case was whether the Republicans had pushed their advantage too far.
In this article, we advocate for a method for evaluating just how perverse a set of legislative districts are. The method relies on the development of a counterfactual—a null distribution of possible redistricting outcomes. To have confidence that an observed map is extreme enough to warrant remedy, it is necessary to characterize a representative distribution of possible redistricting outcomes. In practice, this requires using a computer to draw a large number of alternative maps according to a set of neutral criteria.Footnote 1 In comparing an observed outcome to a large set of neutral alternatives, we may determine the degree to which observed maps differ from what we would expect a neutral process to yield.Footnote 2
We are not the first to propose the principal upon which the method is based nor are we the first to propose an automated process for drawing legislative districts. In 1961, economist and future Nobel laureate William Vickrey posited that it was possible to eliminate “chicanery” from the way legislative districts are drawn. He suggested that a neutral algorithm could solve the redistricting problem, the process of dividing a set of geographic units into a smaller number of districts, in an “automatic and impersonal” way (110). In the years and decades that followed, computers made it possible for scholars to implement methods for developing optimal, neutral maps of legislative districts (see Weaver and Hess Reference Weaver and Hess1963, Nagel Reference Nagel1965, Garfinkel and Nemhauser Reference Garfinkel and Nemhauser1970, Browdy Reference Browdy1990, Bozkaya, Erkut, and Laporte Reference Bozkaya, Erkut and Laporte2003, Chou and Li Reference Chou and Li2006 and Fryer Jr and Holden Reference Fryer Jr and Holden2011). At the same time, analysts recognized that retrieving an unbiased counterfactual of a jurisdiction’s legislative districts is useful in a variety of applications (see Engstrom and Wildgen Reference Engstrom and Wildgen1977, O’Loughlin and Taylor Reference O’Loughlin and Taylor1982, Cirincione, Darling, and O’Rourke Reference Cirincione, Darling and O’Rourke2000, McCarty, Poole and Rosenthal Reference McCarty, Poole and Rosenthal2009, Chen and Rodden Reference Chen and Rodden2013, Chen and Cottrell Reference Chen and Cottrell2016, Fifield et al. Reference Fifield, Higgins, Imai and Tarr2015a, Tam Cho and Liu Reference Tam Cho and Liu2016). In spite of Vickrey’s assertion that developing a neutral process to draw legislative districts would be “not at all difficult” (Reference Vickrey1961, 110), computer-automated redistricting turned out to be at best a challenging problem and at worst an intractable one in complex redistricting scenarios. There are at least two difficulties automated processes encounter; first, an algorithm designed to generate maps of districts may take a biased sample of all possible legislative maps (Altman et al. Reference Altman, Amos, McDonald and Smith2015); and second, many of the most interesting and important redistricting problems are so complex that automated methods may fail to efficiently produce a meaningful distribution of possible alternative maps.Footnote 3
In this article, we present an algorithm that avoids many of the issues related to bias and efficiency exhibited by alternative approaches to automated redistricting. To demonstrate the advantages of our approach, first, we subject the algorithm to tests designed to reveal bias and find no evidence of bias in the way the algorithm draws districts. In one test, we apply the algorithm to a redistricting scenario designed to reveal whether the algorithm we propose produces districts of one variety more often than districts of another variety. We find that it does not. As another test for bias, we compare the sample of maps drawn by the algorithm to a known distribution of possible districts. We find that the algorithm retrieves an accurate approximation of the known distribution. Second, we show that the algorithm we propose is remarkably efficient. Using asymptotic analysis, a technique used by computer scientists to evaluate the complexity of algorithms, we compare our proposed algorithm to a commonly used alternative. We show that our algorithm is many orders of magnitude more efficient than the alternative approach. In short, our contribution is to present an algorithm that retrieves an approximation of the null distribution with no indication of bias in a fraction of the time it takes alternative approaches to produce maps of similar jurisdictions.
To address the redistricting problem, our approach relies on graph partitioning methods developed in computer science. The class of graph partitioning algorithms upon which we base our method are well understood by computer scientists (Kernighan and Lin Reference Kernighan and Lin1970, Hendrickson and Leland Reference Hendrickson and Leland1995, Karypis and Kumar Reference Karypis and Kumar1995, Reference Karypis and Kumar1998); however, applying these processes to the political problem of redistricting is new. In computer science applications, graph partitioning algorithms are used by programmers to divide related computational tasks between a computer’s processor. In our application to politics, we use the algorithm to assign adjacent geographic units to legislative districts.
To further demonstrate the algorithm’s capabilities, we apply it to the substantive problem of congressional districts in a medium (Mississippi), large (Virginia), and very large (Texas) states. These states each have significant minority populations and a history of using the redistricting process to discriminate against those minority groups. We use the algorithm to draw 10,000 maps using census block-level geographic and demographic data. The simulated maps allow us to retrieve a null distribution of the number of majority-minority districts we would expect from a neutral redistricting process within each state. We find that each state’s 2012 congressional map has more majority-minority districts than we would expect from a neutral redistricting process. The finding is significant because, since its decision in Shaw v. Reno,Footnote 4 the Supreme Court has been skeptical of redistricting plans that go to extreme lengths to generate majority-minority districts. Our findings suggest that absent proactive steps on the part of mapmakers, a minority population would be denied the ability to elect “the minority’s preferred candidate”Footnote 5 in the states we analyze.
The article proceeds as follows. In Section 2, we present a method for generating a neutral counterfactual against which existing maps may be evaluated. In Section 3, we evaluate the algorithm for bias and consider the algorithm’s efficiency. Section 4 applies the method to three cases: Mississippi, Virginia, and Texas. In Section 5, we describe how the algorithm could be adapted to account for constraints beyond constitutional requirements of contiguity and population parity. We summarize our conclusions in Section 6 and suggest some further applications of our proposed method of neutral redistricting.Footnote 6
2 A Graph Partitioning Approach to Redistricting
In this section, we propose a method for estimating the distribution of possible maps using a graph partitioning approach. We propose a new algorithm for sampling possible redistricting plans. Finally, we demonstrate how the algorithm would work on a simple redistricting problem consisting of nineteen geographic units and two legislative districts.
2.1 Graph partitioning as a solution to the redistricting problem
Framing redistricting as a graph partitioning problem allows us to simplify the process of drawing maps. As a result, we can generate a set of neutral maps of legislative districts under the constitutional constraints that districts be contiguous and contain equal populations. We conceive of a map as a undirected vertex-weighted graph in which vertices are weighted according to population, but edges are assigned no meaningful weight.Footnote 7
Our approach can be summed up as follows: First, we convert the geographic data into a graph where every geographic unit becomes a vertex weighted by the population of the geographic unit. The graph’s edges represent shared borders between geographic units. We then partition the graph (a simpler version of the graph derived from the map) into the required number of districts that meet the legal requirements of being both contiguous and containing equal population. Since it is often infeasible to have districts that are exactly balanced, the algorithm is satisfied by districts with populations that neither exceed nor fall below certain bounds.
2.2 An algorithm for drawing neutral districts
The algorithm we propose for achieving a contiguous and balanced partition has four steps.Footnote
8
First, the algorithm coarsens the graph, grouping together connected vertices of the graph into contiguous multinodes. Second, the algorithm partitions the multinodes of this simplified graph into the desired number of contiguous districts using a breadth first search. Third, it uncoarsens the graph, so that the graph is again made up of the original vertices, but all vertices are now associated with a particular district from the previous step. Finally, it refines the graph by moving vertices into and out of districts until the populations of the districts are balanced. Refinement continues until either the established tolerances are met, or the graph ceases to become more balanced.Footnote
9
We consider a weighted graph
$G_{0}(A_{0},E_{0},w)$
where
$w$
is a function that maps
$A_{0}$
onto a set of weights. We limit our discussion to the intuition behind the algorithm and provide a formal description of our proposed process in appendix A.
Step 1 (“Coarsening”)
We transform
$G_{0}$
into a series of smaller graphs
$G_{1},G_{2},G_{3},\ldots ,G_{m}$
where vertices in
$G_{t}$
are consolidated into multinodes in
$G_{t+1}$
. These multinodes are an intermediate construct that allow the algorithm to perform a more efficient partition, but they do not represent a politically meaningful unit. The number of multinodes is not particularly important, and neither do they have to be particularly balanced. The important thing is that they are internally contiguous, and that they are not too uneven.Footnote
10
In our case, since the graph has unweighted edges, the algorithm randomly selects an initial vertex.Footnote 11 The algorithm then selects vertices from among the neighbors of that vertex and joins those vertices into a multinode. The algorithm repeats this process until all vertices are assigned to one of several multinodes. The intention is to simplify the graph in order to simplify the problem of partitioning the graph. Critically, all the information of a multinode’s constituent nodes, their connection to other vertices and their weight, is preserved when vertices are collected into multinodes. Thus one multinode is adjacent to another multinode if at least one constituent vertex in each are adjacent to one other. Likewise, the weight of a multinode is the sum of the weights of its constituent nodes.
Step 2 (“Partitioning”)
Once the graph has been simplified, the algorithm generates partition
$P_{m}$
. It randomly selects a multinode with which to start. It then selects a neighboring multinode to add to the district and continues to add randomly selected neighbors until roughly
$1/k$
of the available weight is in the district where
$k$
is the number of districts into which the vertices (multinodes) should be divided.Footnote
12
The algorithm discards discontiguous graphs that result when the process yields a set of multinodes that cannot be joined because they are separated by contiguous districts.
Step 3 (“Uncoarsening”)
In series of steps, the algorithm reverses the aggregating process that yielded
$G_{m}$
. At the beginning of each step
$t$
, the constituent elements of multinodes in
$G_{t-1}$
preserve their assignment to a particular district in
$P_{t-1}$
.
Step 4 (“Refinement”)
Generally speaking, the purpose of this step is to make each component of a partition
$P_{t}$
as balanced as possible. At each step of uncoarsening the algorithm reassigns elements of one district into an adjacent district if reassignment would bring the districts closer to weight parity. This requires the implementation of an additional balancing algorithm to determine which elements of a partition should be (or should not be) reassigned. In practice, there exist several algorithms that can refine the graph into a more balanced partition in the way we describe. We apply one of these, the Kernighan–Lin algorithm (KL) (Hendrickson and Leland Reference Hendrickson and Leland1995, Kernighan and Lin Reference Kernighan and Lin1970), to refine the graph at each step of uncoarsening. KL is a widely used algorithm for balancing graphs in computer science since it accounts for the weights of vertices and edges as it seeks to produce a more balanced map.Footnote
13
Step 5 (“Repeat”)
This step is the easiest of all, as it is just a check to see if the partition meets the required balance (population equality) conditions. If the resulting partition is a set of contiguous and balanced districts, we record the partition for later analysis. If not, the flawed partition is discarded and the algorithm restarts.
2.3 An example
Consider a simple application of our method of drawing legislative districts to a set of nineteen contiguous geographic units represented in Figure 1(a). The goal is to partition this map into a plan with two contiguous districts in which the population of both districts is balanced. The set of geographic units represented in Figure 1(a) is globally contiguous—that is, every unit in the map could potentially be included in a contiguous district with any other unit in the map. The algorithm proceeds by, first, simplifying the map into a connected graph with nineteen vertices and thirty-nine edges; second, collecting vertices into an even simpler graph; third, partitioning the simpler graph; and finally, refining the graph to ensure that the resulting districts have balanced (equal) populations. In this example, the result of this process is a single “partition” of the map into a set of two districts with equal populations.
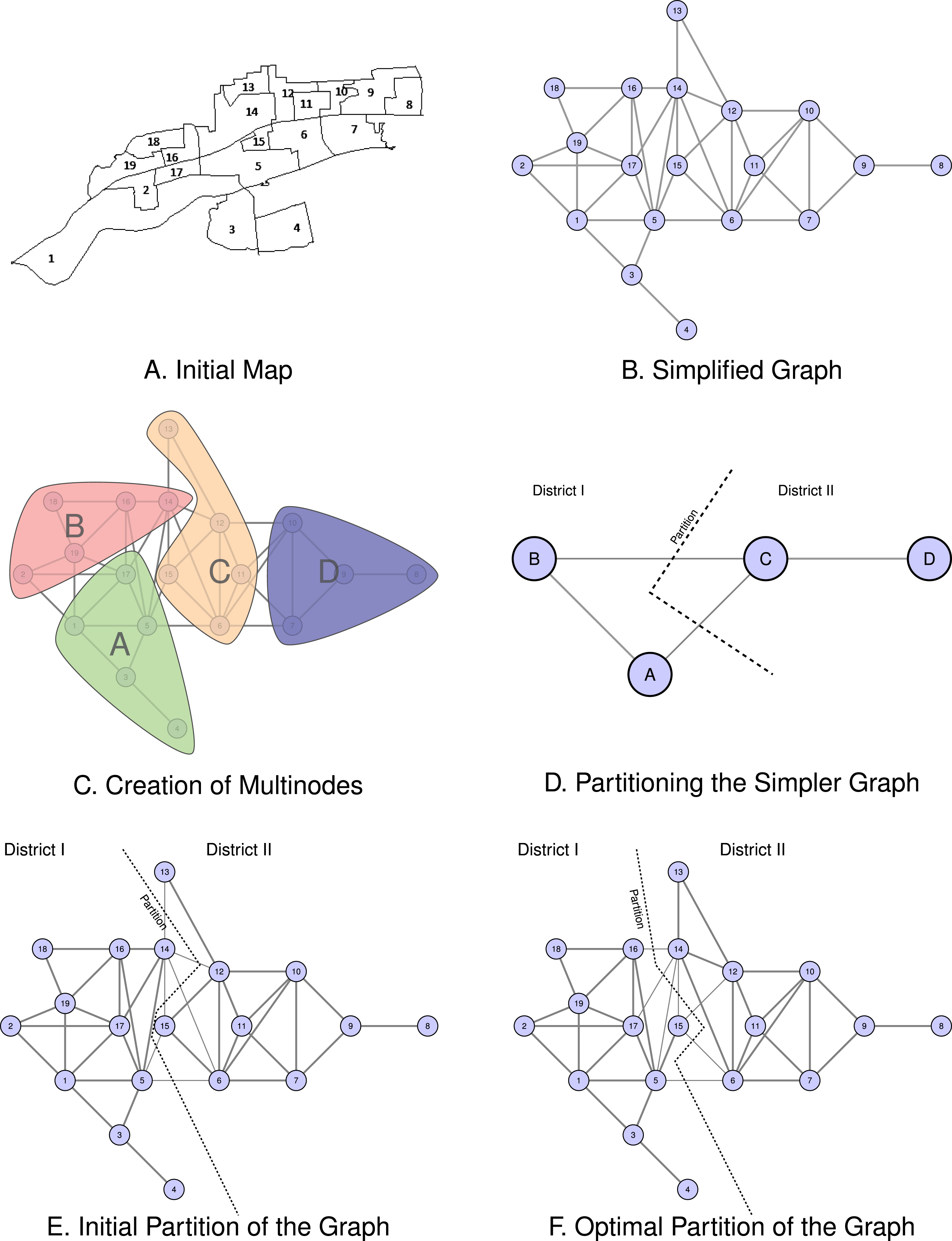
Figure 1. An example of how the algorithm partitions a map consisting of nineteen contiguous geographic units.
First, the algorithm begins by simplifying the map into a connected graph. Using the map in Figure 1(a), we may determine which geographic units share any portion of its border with any other geographic unit.Footnote 14 We represent the simplified graph of the map in Figure 1(b). Each geographic unit is represented as a circular node. An edge (line) connects the vertex representing a unit to the vertex representing other units with which it is contiguous. In this simplified version of the original map, there are nineteen vertices connected by thirty-nine edges. This representation of the map preserves all of the information necessary for generating contiguous districts.
Second, the algorithm randomly collects vertices into multinodes creating a simpler graph. In the example, the algorithm assigns groups of four or five vertices to one of four multinodes. We represent this process in Figure 1(c). Each of the vertices assigned to a multinode shares an edge with at least one vertex in the multinode making each multinode internally contiguous. We index these multinodes as
$A$
,
$B$
,
$C$
, and
$D$
. The process of collecting these vertices into multinodes is random, so in any iteration of the algorithm, we can expect that two neighboring vertices will end up in different multinodes with positive probability. Observe that if two multinodes have constituent vertices that were contiguous in Figure 1(b), those multinodes are contiguous in Figure 1(c). That is, the multinodes preserve the contiguity of their constituent nodes.
Third, the algorithm partitions the simpler graph. It assigns each multinode (and the multinode’s constituent nodes) to a district. This process is represented in Figure 1(d). Here, the algorithm generates the partition
$\{A,B\},\{C,D\}$
. Note that not all combinations of these multinodes would be valid. While
$A$
,
$B$
, and
$C$
are all contiguous, the vertices in
$D$
are only contiguous with vertices
$C$
.
Finally, the algorithm refines the graph in order to ensure that the resulting districts have balanced (equal) population. The graph partitioning problem represented in Figure 1(d) is significantly simpler than the problem of finding a valid partition of the graph in Figure 1(b) with nineteen nodes, but this comes at the cost of balance. Since the multinodes were generated randomly, the partition represented in Figure 1(d) is not likely to be balanced. We represent the process of refining the partitioned graph in figures 1(e) and 1(f). Kernighan–Lin swaps randomly selected vertices across the border generating an alternative partition. If the alternative partition is closer to balanced than the initial partition, it keeps the alternative and throws out the initial partition. It stops once switching vertices does not generate a more balanced graph.
We limit our example to the generation of a single partition of the map in Figure 1(a); however, analysis of observed maps requires that we compare those maps to a neutral counterfactual. Since the process of creating multinodes began with the random selection of a vertex to which adjacent vertices were added, each time we repeat the algorithm in a large enough graph, we arrive at an alternative, balanced partition with positive probability. Since the algorithm only considers the contiguity and weight (population) of each node, the result is a distribution of neutrally drawn districts.Footnote 15 We can then compare the actual set of legislative districts to the distribution of districts we observe and characterize the probability that the actual partition created would have emerged from a neutral process.
3 Bias and Efficiency
The algorithm we describe in the previous section avoids many of the shortcomings of alternative algorithms. Specifically, we find no evidence of bias in the way the algorithm draws districts. We subject our proposed algorithm to two tests for bias. The first test is designed to reveal if the algorithm we propose produces districts of one variety more often than districts of another variety. We find that it does not. The second test is designed to evaluate the algorithm’s ability to retrieve an approximation of the underlying distribution of possible districts. We compare a large sample of maps drawn by the algorithm to a known distribution of possible districts. We find that the distribution of maps the algorithm retrieves is very similar to the known distribution.
In this section, we also demonstrate that our proposed algorithm is remarkably efficient. Using asymptotic analysis, a technique used by computer scientists to evaluate the complexity of algorithms, we compare our algorithm to a commonly used alternative proposed by Cirincione, Darling, and O’Rourke (Reference Cirincione, Darling and O’Rourke2000). We show that the algorithm we propose is many orders of magnitude more efficient than the alternative approach.
3.1 Bias
In order to evaluate the possibility that our proposed algorithm draws maps in a biased way, we apply the algorithm we propose for drawing districts to a problem for which we know the solution (Altman, Gill, and McDonald Reference Altman, Gill and McDonald2004). First, to show that our proposed algorithm does not produce districts of one variety more often than districts of another variety, we apply our algorithm to a square (
$100\times 100$
) geographic space with 10,000 units all of which contain the same number of people and evaluate the resulting maps to see if one type of district is more likely than others. We find that one type of district is not more likely than another. Second, to evaluate the algorithm’s ability to approximate the underlying distribution of possible districts, we apply the algorithm to a much simpler space for which we know the true distribution of possible districts. We find that the algorithm approximates the true distribution.
3.1.1 Bisecting a symmetrical space
Demonstrating bias in a sample from a distribution as large and complex as the set of possible electoral maps is a complicated proposition. In practice, the geographic units that constitute the basis of jurisdictions’ electoral maps have irregular populations and have varying numbers of neighbors to which they are adjacent. One way to approach the problem is to consider a case for which we know the characteristics of an unbiased sample. In this instance, we partition a hypothetical symmetrical set of geographic units with equal population. Since it is identical vertically and horizontally, we should observe that the number of maps that bisect the space horizontally should be close to equal to the number of maps that bisect the space vertically. Altman et al. (Reference Altman, Amos, McDonald and Smith2015) propose a similar test using a smaller grid, and they find that several commonly used redistricting algorithms are more likely to produce one type of map than another. We implement the test on a large grid containing roughly the number of units in a medium-sized state’s map of electoral precincts.Footnote 16
Consider a square geographic space with 10,000 units that each contain the same number of residents. For simplicity, suppose that there are two possible outcomes of the process: districts that bisect the space horizontally and districts that bisect the space vertically. Observe that such a space is symmetrical vertically and horizontally. If the goal is to divide such a space into two districts with equal population, an unbiased process should be as likely to bisect the space horizontally as it is to bisect the space vertically. We apply our proposed algorithm to this simple problem. First, we partition a grid of
$100\times 100$
(10,000) units 1 million times (Magleby and Mosesson Reference Magleby and Mosesson2017). Next, we determine how many districts bisect the space horizontally, how many bisect the grid vertically.
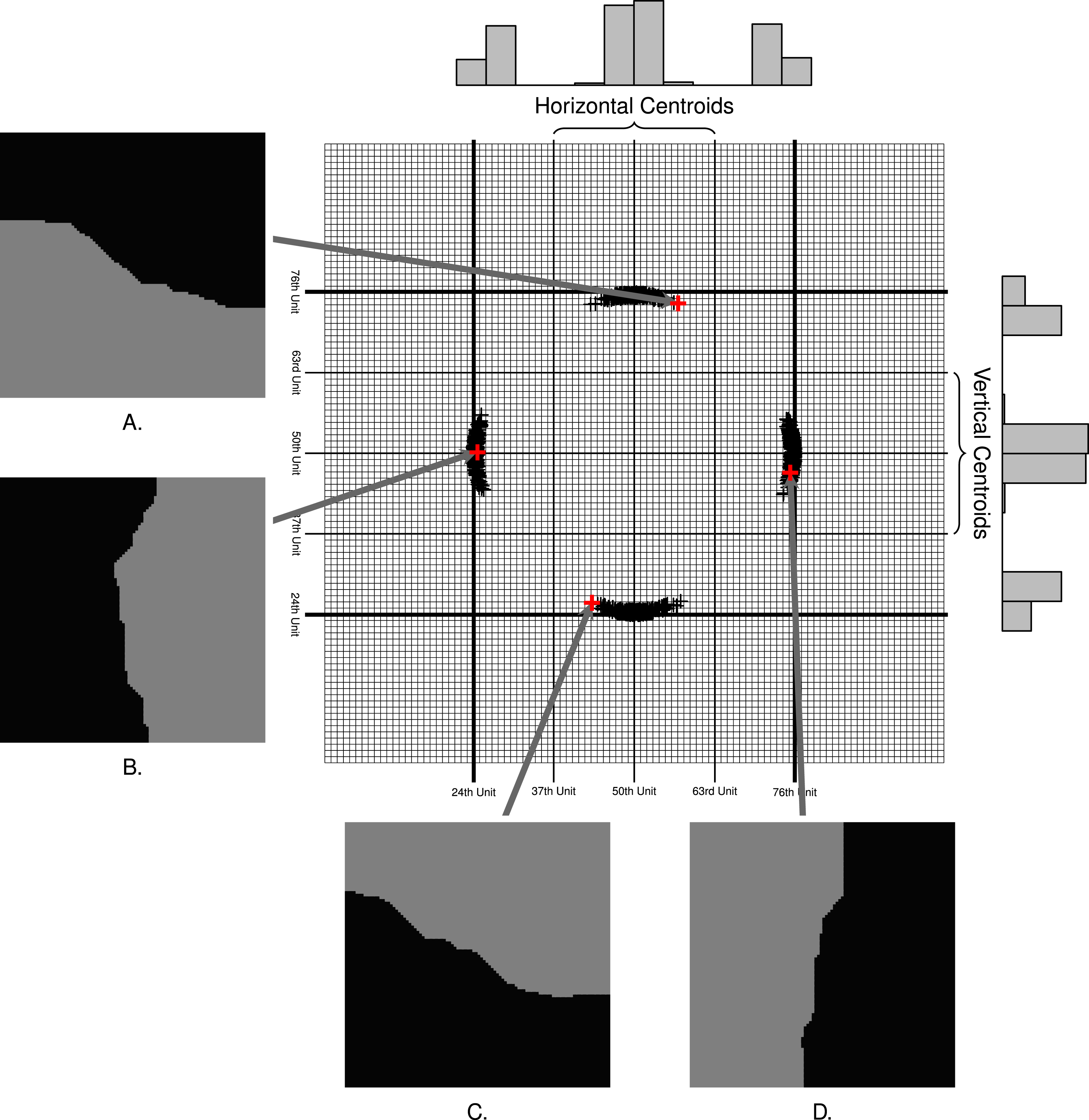
Figure 2. Plot of centroids for 10,000 two-way partitions of a
$100\times 100$
grid of geographic units with equal population. If the algorithm draws uniformly from the distribution of all possible districts, horizontally oriented districts (like examples
$A.$
and
$C.$
) should be as likely as vertically oriented districts (like examples
$B.$
and
$D.$
). We indicate the location of the darker district’s centroid in the plot with a lighter colored
$+$
symbol.
In Figure 2 we plot the centroid of one district from 1,000 two district maps produced by the algorithm from the hypothetical grid. Examples
$A$
,
$B$
,
$C$
, and
$D$
in Figure 2 represent the types of bisections the algorithm produces. Each bisection has a darker and lighter “district”, and we include arrows that point to the location of the darker district’s centroid on the example grid. Above the plot, we include a histogram representing the density of observed centroids on the
$x$
-axis. To the right of the plot, we include a histogram of the density of observations on the
$y$
-axis. While not identical, these distributions are very similar for the 1,000 observations by visual examination.
Observe that all centroids fall between the 24th and 76th units on the
$x$
-axis and
$y$
-axis. To identify horizontally and vertically oriented plans, we divide the range of centroids on each dimension into three regions. We consider districts with centroids between the 37th and the 63rd unit on the
$x$
-axis to be horizontal. In like manner, we consider districts with centroids between the 37th and the 63rd unit on the
$y$
-axis to be vertical. If the algorithm produces maps in an unbiased way, then half the maps should have districts with centroids in the vertical region and half the maps should have districts with centroids in the horizontal region.
In 1 million trials, we find that 500,644 maps have a vertical orientation (a centroid in the region between the 37th and the 63rd unit on the
$y$
-axis) and 499,356 have a horizontal orientation (centroid in the region between the 37th and the 63rd unit on the
$x$
-axis). The resulting proportion of maps with vertically oriented districts (0.500644) is not statistically different from 0.5, our expected result from an unbiased process (
$\unicode[STIX]{x1D712}^{2}=1.659$
,
$p=0.1977$
). Thus, we fail to find statistically significant evidence of bias in the orientation of the 1 million maps created by the algorithm. In addition, we only observe a small substantive difference (0.0006) from what we would expect from an unbiased mapmaking process.
3.1.2 Sampling from a known distribution
We apply our algorithm to a small jurisdiction consisting of twenty-five geographic units made available by Fifield et al. (Reference Fifield, Higgins, Imai and Tarr2015b). We set the algorithm to partition the space into three districts with populations that deviate by no more than 10% from population parity (Magleby and Mosesson Reference Magleby and Mosesson2017). We then compare the distribution of maps produced by the algorithm we propose to the distribution of all possible maps of the jurisdiction provided by Fifield et al. (Reference Fifield, Higgins, Imai and Tarr2015b). A Kolmogorov–Smirnov (KS) test indicates that the two distributions are not exactly the same;Footnote
17
however, we find that the distribution of maps retrieved by our process approximates the true distribution enumerated by Fifield et al. for maps balanced to 10% population parity. On the other hand, when we constrain our analysis to maps that meet more standard levels of population parity (
$\pm 1.5\%$
), a KS test does not permit us reject the null hypothesis of equivalence between the distribution of possible balanced maps and the distribution of balanced maps drawn by the algorithm we propose.
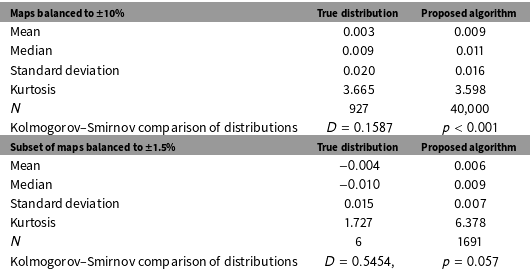
Table 1. We summarize a comparison of the mean, median, standard deviation, and kurtosis of the true distribution of partisan skew of all possible maps containing districts that deviate by no more than 10% (
$N=927$
) to the distribution of maps drawn by the algorithm we propose that in which the district population deviates by no more than 10% (
$N=40,000$
). Below, we summarize the comparison between the mean, median, standard deviation, and kurtosis of all possible maps containing districts that deviate by no more than 1.5% (
$N=6$
) to the distribution of maps drawn by the algorithm we propose in which the district population deviates by no more than 1.5% (
$N=1691$
).
To summarize the maps’ characteristics, we focus on the level of partisan skew in each map, specifically the skew in the distribution of Democratic votes across districts in a map.Footnote
18
We consider partisan skew in the set of possible maps, as reported by Fifield et al. (Reference Fifield, Higgins, Imai and Tarr2015b), balanced to
$\pm 10\%$
to a set of maps drawn using our proposed algorithm also balanced to
$\pm 10\%$
we then repeat the comparison for the more realistic level of partisan parity,
$\pm 1.5\%$
. In Table 1, we compare four characteristics of the true distribution of partisan skew along to the same four characteristics of the distribution of partisan skew of the maps drawn by the algorithm we propose. While characteristics of the distribution of maps produced by the algorithm approximate the characteristics of the distribution possible maps, the distributions are not exactly equivalent. In Table 1, we include the Kolmogorov–Smirnov (KS) statistic for the comparison between the distribution recovered by the algorithm we propose and the true distribution as reported by Fifield et al. (Reference Fifield, Higgins, Imai and Tarr2015b). The KS test yields a test statistic of 0.1587. Thus, we can reject the null hypothesis that the distribution of maps produced by the algorithm is exactly the same as the distribution enumerated by Fifield et al. (Reference Fifield, Higgins, Imai and Tarr2015b).
Important caveats apply to the comparisons summarized in Table 1. First, the KS test indicates that the two distributions are not identical; however, this finding should not be construed to mean that the sample of maps created by the algorithm does not approximate the distribution of all possible maps. The two distributions are very similar, but we cannot claim that they are equivalent. Second, the set of maps enumerated by Fifield et al. (Reference Fifield, Higgins, Imai and Tarr2015b) is not particularly balanced, that is, the population deviation between the largest and smallest districts in the set of possible maps is relatively large (
$\pm 10\%$
).Footnote
19
In the bottom panel of Table 1 we present the characteristics of the set of maps in Fifield et al.’s data that are balance to a more typical level of population deviation (
$\pm 1.5\%$
). We likewise present summary statistics from the subset of maps produced by the algorithm that conforms to the more typical population constraint (1691/40,000). The comparison is informative in that it shows how few of the possible maps in Fifield et al.’s data achieve standard levels of population parity (
$6/927$
). As with the larger sets of maps, the distributions of maps approximate one another. In contrast to the comparison between the larger sets of maps, the KS test does not show a significant difference between the set of possible maps with population parity and the set of subset of maps produced by the algorithm with population parity (
$p=0.057$
). In sum, the KS test does not permit us reject the null hypothesis of equivalence between the distribution of possible balanced maps and the distribution of balanced maps drawn by the algorithm we propose.
3.2 Efficiency
In addition to showing no indication of bias, the algorithm we propose is extremely efficient. We demonstrate the algorithm’s efficiency by considering its algorithmic complexity and show how that complexity scales with the complexity of the redistricting problem. Once we understand the algorithmic complexity of our process, it is possible to contrast the algorithm to the process proposed by Cirincione, Darling, and O’Rourke (Reference Cirincione, Darling and O’Rourke2000), a commonly used alternative. While other automated redistricting processes exist, Cirincione, Darling, and O’Rourke’s process is a useful comparison because it is acknowledged to be the “representative” redistricting algorithm (see Altman et al. Reference Altman, Amos, McDonald and Smith2015, Fifield et al. Reference Fifield, Higgins, Imai and Tarr2015a).Footnote 20 We show that, for practically all redistricting problems, the algorithm we propose should outperform the commonly used alternative.
An asymptotic analysis of the algorithm we propose characterizes its algorithmic complexity and demonstrates how that complexity scales with the complexity of the redistricting problem. We may conceive of the algorithm we describe as a function that maps some number of geographic units,
$n$
, into some number,
$D$
, of contiguous electoral districts. By analyzing the asymptotic behavior of the function that describes the algorithm, we determine the way that processing time will increase as the redistricting problem becomes more complex holding computational resources constant. The redistricting problem becomes more complex as either
$n$
or
$D$
or both increase. In Appendix B we show that the algorithm we propose scales according to the following function.
$$\begin{eqnarray}\displaystyle f(n,D)=n^{2}\log nD\log D. & & \displaystyle\end{eqnarray}$$
The contour plot in Figure 3(a) represents the way that (1) scales for different values
$n$
(
$x$
-axis) and
$D$
(
$y$
-axis). Each line represents the
$\log _{10}$
of constant runtime. For example, we show in the graph that the algorithm should take the same amount of time to divide 100,000 units into 120 districts as it would take to divide 600,000 units into ten districts. The absolute value of the numbers associated with each contour line is less important than the relative increase. The graph indicates that, holding
$D$
constant, the algorithm’s runtime increases in
$n$
. The same is true in reverse: holding
$n$
constant, the marginal impact on expected runtime increases with each additional district. Take the case of a state legislature with 100 members of its lower house. Our asymptotic analysis suggests that if it took 0.01 seconds to draw a map of 100 districts from roughly 100,000 geographic units, it would take about 0.1 second to draw a map of 100 districts from roughly 300,000 geographic units, and it would take 1.0 seconds to draw a map of 100 districts from 850,000 geographic units.
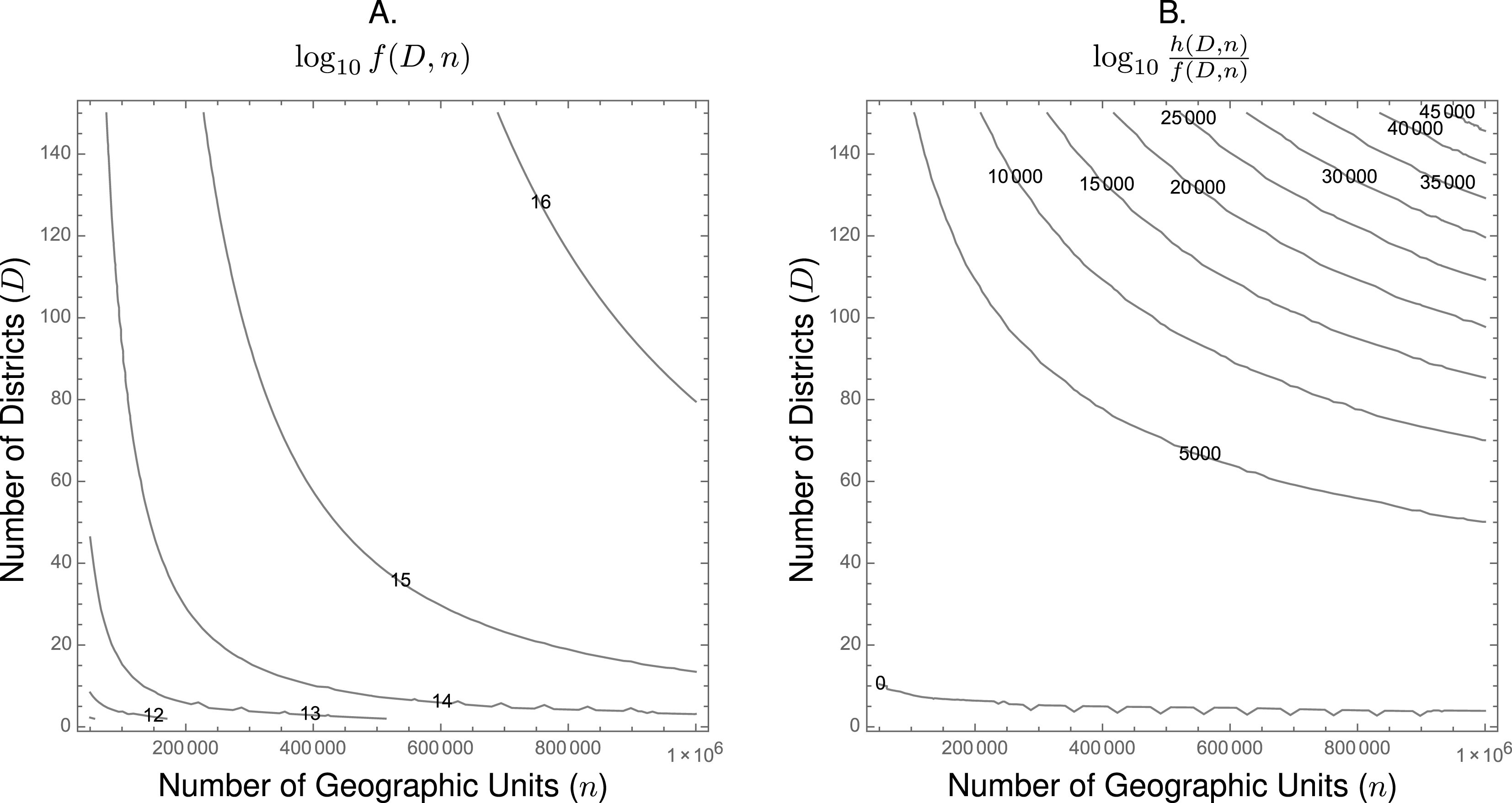
Figure 3. (a) The manner in which the algorithm we propose scales with the number of districts (
$D$
) and the number of geographic units (
$n$
), and (b) a comparison of algorithmic complexity of our proposed algorithm to the algorithm proposed by Cirincione, Darling, and O’Rourke (Reference Cirincione, Darling and O’Rourke2000). The
$x$
-axis in both graphs represents the number of geographic units (
$n$
) that the algorithm takes as an input, and the
$y$
-axis represents the number of districts (
$D$
) that the algorithm creates from those geographic units. The lines represent orders of magnitude in difference in asymptotic runtime at corresponding values of
$D$
and
$n$
.
The computational efficiency of the algorithm we propose becomes particularly important when compared to other algorithms devised to address the same redistricting problem. For example, take a commonly used alternative redistricting algorithm proposed by Cirincione, Darling, and O’Rourke (Reference Cirincione, Darling and O’Rourke2000). In Appendix B we show that their algorithm scales according to the following function.
$$\begin{eqnarray}\displaystyle h(n,D)=\frac{n}{\mathop{\prod }_{1}^{D-1}p(n,i)}, & & \displaystyle\end{eqnarray}$$
where
$p(n,i)$
is the probability that the next iteration will successfully yield a contiguous district.Footnote
21
The differences between (1) and (2) may not be immediately apparent, so we represent ratio of expected runtimes for values of
$n$
and
$D$
in Figure 3(b). Here, the contour lines represent the difference in runtime (in orders of magnitude) between our proposed algorithm and this commonly used alternative.Footnote
22
The contour line labeled
$0$
are the values of
$n$
and
$D$
for which we expect no difference in runtime between the two algorithms. From Figure 3(b), it is clear that our proposed algorithm outperforms the alternative algorithm for all redistricting problems except those for which the
$n$
or
$D$
is very small.
The difference between the two algorithms is stark when either is applied to jurisdictions with larger
$n$
and more
$D$
. For example, consider the redistricting problem for New York’s State Assembly. There are 150 Assembly districts in New York (
$D=150$
).Footnote
23
If an analyst were to use census blocks as the geographic unit from which he or she drew districts, then
$n=350,169$
census blocks in New York in the 2010 census. Thus, we expect that the runtime for our algorithm would be between 10,000 and 15,000 orders of magnitude faster than the processing time of the Cirincione, Darling, and O’Rourke (Reference Cirincione, Darling and O’Rourke2000) algorithm when using census block data to draw state assembly districts in New York. Perhaps more concretely, suppose our proposed algorithm could draw a map of 150 districts from New Yorks 350,169 census blocks in 1.0 second. Asymptotic analysis indicates that Cirincione, Darling, and O’Rourke’s algorithm would take longer than
$317\times 10^{9990}$
years to draw one map of New York’s 150 districts from its 350,169 census blocks.
4 Demonstration
Texas, Virginia, and Mississippi provide an excellent context in which to apply the algorithm we propose. All three states have significant minority populations, and all three states are located in the South. Prior to the Supreme Court ruling that invalidated Section 5 of the Voting Rights Act, all three states had to submit their redistricting plans to the Justice Department for preclearance.Footnote 24 Following the Court’s decision in Thornburg v. Gingles,Footnote 25 which encouraged the creation of districts in which minority population made up more than half the population, all three states took steps to create majority-minority districts. We consider several types of majority-minority districts. For the purposes of our analysis, we consider majority-minority districts in Mississippi and Virginia to be districts in which the US Census data categorizes 50% or more of the residents as “Black or African American alone”. In Texas, we consider districts in which the census categorizes 50% or more of the residents as “Hispanic or Latino” to be majority-minority districts.Footnote 26 Given the large minority populations in Texas (12.5% Black, 38.6% Hispanic), Virginia (19.7% Black, 8.9% Hispanic), and Mississippi (37.5% Black, 3% Hispanic) each state is a prime candidate for producing at least one majority-minority district.
4.1 Summary statistics
The goal of our analysis is to develop an approximate expectation of the distribution of minority residents between a state’s districts if legislative mapmakers only consider contiguity and population. In practice, the geographic distribution of minority voters and the political and legal contexts in which the congressional districts are devised influences the number of majority-minority districts within a state. Since our proposed algorithm only considers contiguity of geographical units and the total population of those units, it is neutral with regards to the politics or race of the individuals living in a given geographical unit. Consequently, the algorithm is neutral with regards to the output of the process. Since the algorithm generates each map by a different neutral and random process, the probability that any two maps are exactly alike is extremely small. The distribution of maps represents the counterfactual against which we can compare the actual map generated by the states we analyze. The distribution also allows us to characterize the approximate probability by which the states’ maps could have emerged from a neutral process. Of course, mapmakers in each state strove to comply with the Court’s encouragement to generate majority-minority districts. Whether out of zeal to fulfill the courts instructions or out of some other motivation, each state in our analysis deviates in significant ways from a neutral process of drawing districts.
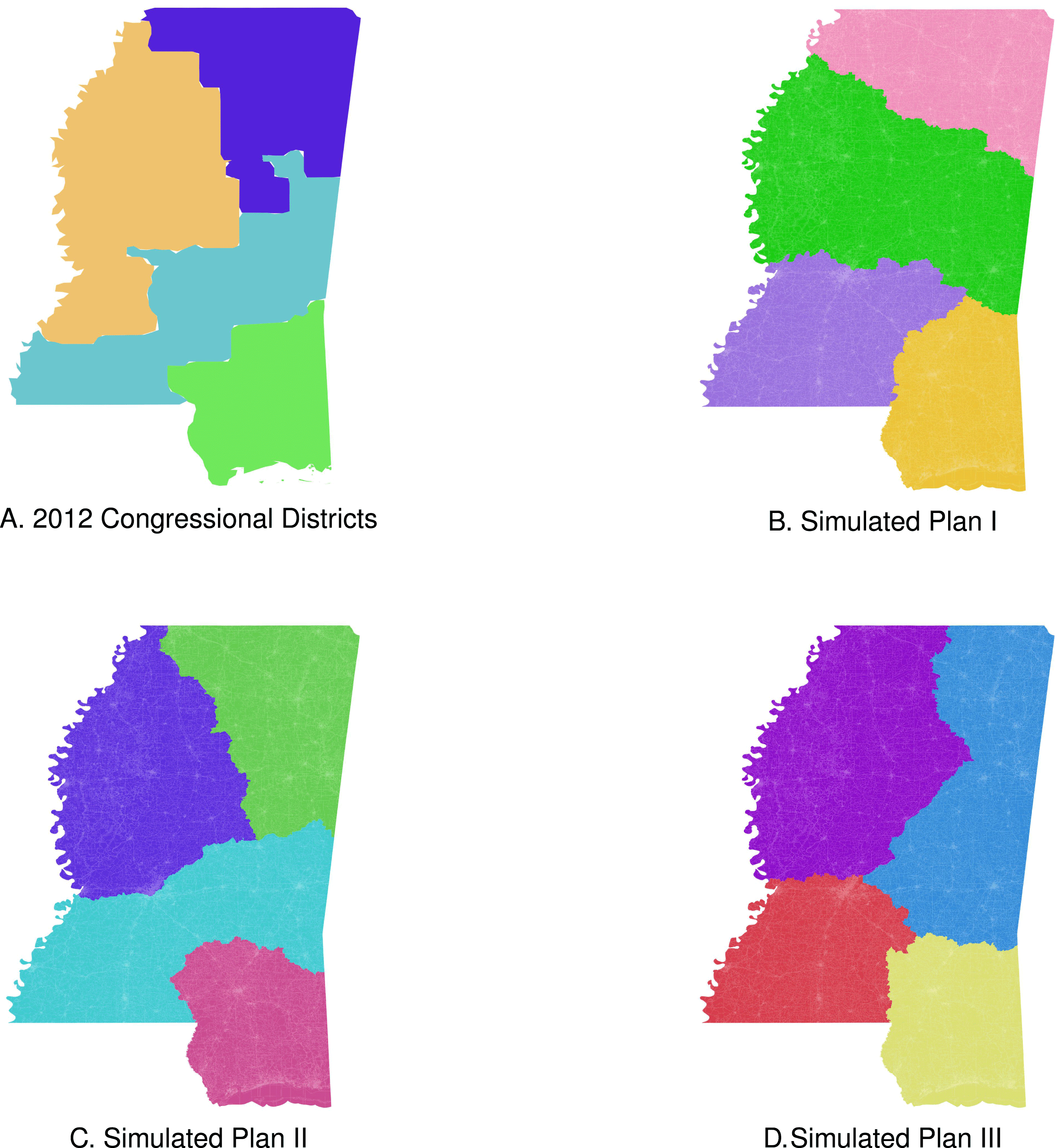
Figure 4. Three neutral maps of Mississippi exhibit the types of variation typical of our neutral mapping algorithm.
To draw our neutral maps, we use data collected by the United States Census and made available by the Minnesota Population Center’s National Historical Geographic Information System (NHGIS) project. We use census block-level geospatial and demographic data. Census blocks are the smallest geographic unit for which we have information regarding population and reliable data regarding residents’ demography. We generated 10,000 maps of four, eleven, and thirty-six congressional districts for Mississippi, Virginia, and Texas, respectively (Magleby and Mosesson Reference Magleby and Mosesson2017). Representations of the kinds of districts the algorithm produces are visible in Figures 4, 5, and 6. In Figures 4(a), 5(a), and 6(a), we include the actual map of districts that each state used for the 2012 congressional elections. As is clear from Figures 4, 5, and 6, the algorithm generated relatively compact districts. Each was balanced to within 1.5% of the ideal for that state. The examples of neutral partitions of Mississippi included in Figure 4 show how the maps generated by the algorithm diverge from the actual map used for the 2012 elections. Just as the actual plan does, the maps represented in Figures 4(b) and 4(c) divide Jackson, one of the only urban areas in Mississippi, across two districts. By contrast the map in Figure 4(d) keeps Jackson whole. Each example is a valid partition of Mississippi into four contiguous districts with roughly equal population.
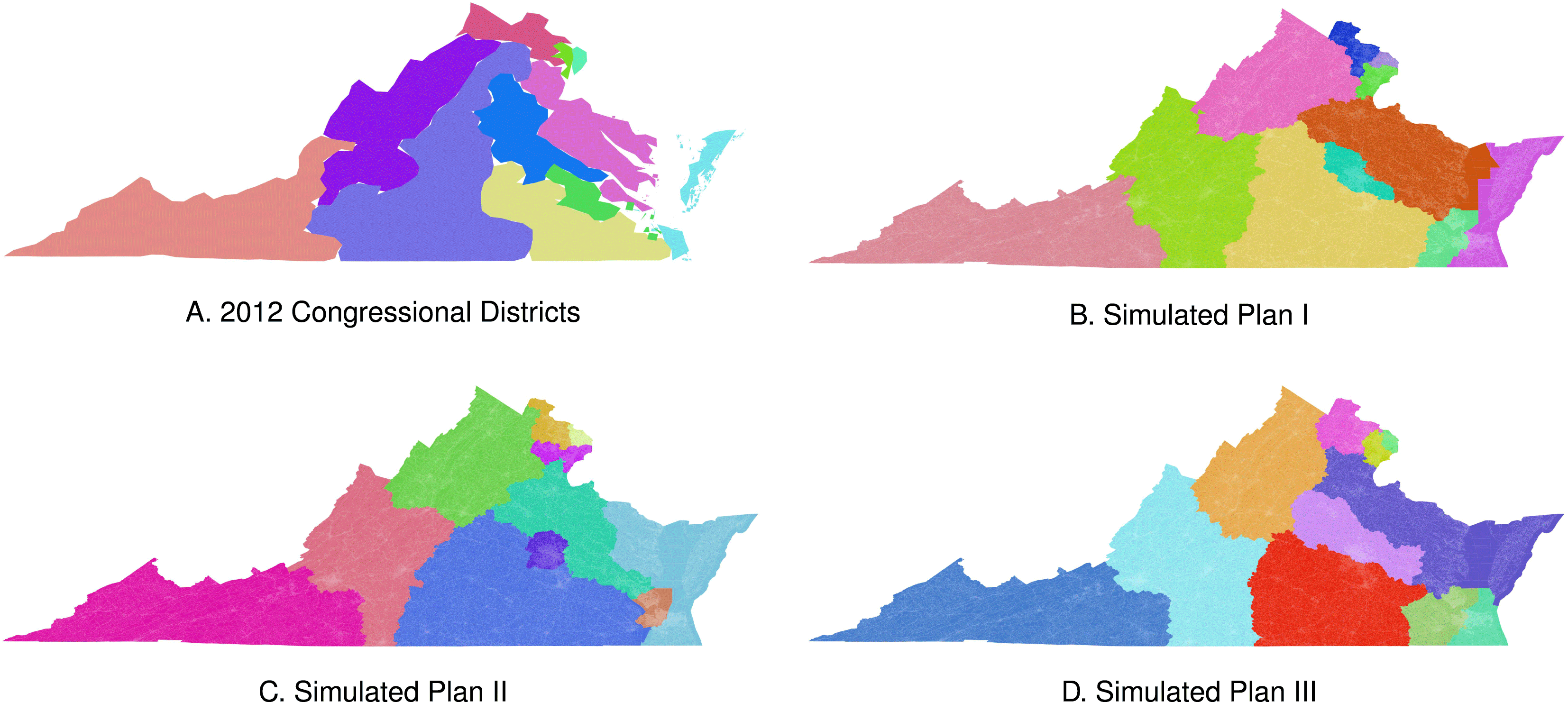
Figure 5. Three neutral maps of Virginia exhibit the types of variation typical of our neutral mapping algorithm.
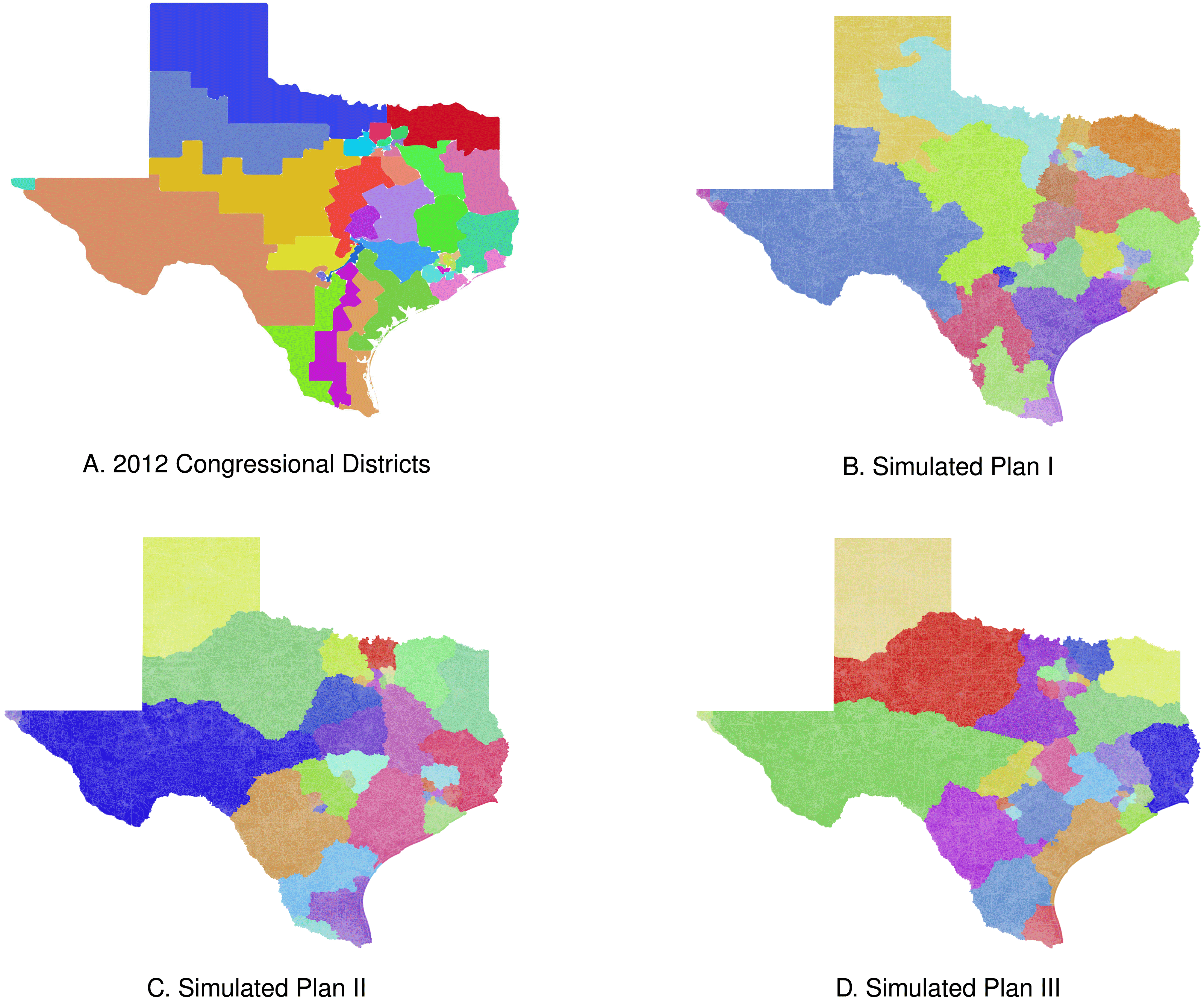
Figure 6. Three neutral maps of Texas exhibit the types of variation typical of our neutral mapping algorithm.
The algorithm also generated realistic districts in the larger state Virginia that show considerable variance in the composition of districts. Just like the actual map, the maps in Figures 5(b)–(d) show multiple districts in the densely populated areas around Washington, DC in Northern Virginia, but each of the example maps handled the other densely populated areas in and around Richmond and Hampton differently. Again, our proposed algorithm only considers population and contiguity, so these example maps represent realistic, balanced, and neutral partitions of Virginia into eleven congressional districts.
Finally, the algorithm generated a variety of realistic maps of Texas’s congressional districts. The actual map, included here as Figure 6(a), has several districts in the densely populated Dallas, Houston, and Austin areas. Figures 6(b)–(d), all have a geographically small districts in these more densely populated areas. Just like the actual map, each simulated map included here has a smaller district in the far west El Paso area, and geographically expansive districts covering sparsely populated West Texas and the Texas panhandle regions. One contrast between the simulated maps and the map in Figure 6(a) is the way the simulated maps deal with the highly hispanic region of South Texas. Texas’s 2012 map divides this heavily Latino area into three districts that run from the border with Mexico to Austin. The actual districts in this region are heavily hispanic leaving neighboring districts with fewer latino voters. The algorithm drew the examples in Figures 6(b)–(d) without reference to race and divide up the heavily hispanic population of South Texas neutrally. For some of these neutral maps, the result may be a more even distribution of hispanic residents across more than three districts in South Texas.
4.2 State performance
The algorithm retrieves an approximate null distribution of the number of majority-minority districts in each of the states we examine. That is, it allows us to create an expectation of the number of majority-minority districts in each state had mapmakers only considered population and the contiguity of geographic units that make up the district. Using census data on the racial composition of each state’s actual congressional districts, we characterize the degree to which the racial composition of each state’s actual districts differ from the neutral counterfactual retrieved by the algorithm. In the most recent round of redistricting following the 2010 census, blacks constituted a majority of the residents in one out of four congressional districts in Mississippi, two out of eleven congressional districts in Virginia. Hispanic residents were a majority in nine out of thirty-six districts in Texas.
Table 2. A comparison of the actual number of majority-minority districts in Mississippi, Virginia, and Texas and estimates of the number of majority-minority districts in 10,000 simulated maps of congressional districts. Data on district and block-level demographics taken from the US Census data provided by NHGIS.
a Proportion of residents categorized as “Black or African American alone” greater than 0.5.
b Proportion of residents categorized as “Hispanic or Latino” greater than 0.5.
The data summarized in Table 2 provide an expectation of the number of majority-minority seats each state should produce. Those data indicate the probability that the actual number of majority-minority districts in Mississippi, Virginia, and Texas arose from a neutral process. In Mississippi, fewer than
$1/3$
of the simulated maps produced one majority black seat. We may interpret the frequency of majority-minority seats in our simulated maps of Mississippi, 3,073
$/$
10,000 produced one majority black seat, to mean that there is less than an approximately 30.73% chance that the number of majority-minority districts we actually observe in Mississippi arose from a neutral process. In Virginia, none of the 10,000 neutrally drawn maps produced a majority black district. Thus we can say that there is less than an approximately 0.001% chance that the actual map of Virginia’s congressional district arose from a neutral process. Finally, 1,589
$/$
10,000 of our neutrally drawn maps of Texas produced nine or more majority hispanic districts. Thus, we may say that there is less than an approximately 16% chance that the actual map of Texas’s congressional districts arose from a neutral process. In short, we cannot confidently reject the notion that Mississippi (
$p<0.3073$
) and Texas (
$p<0.1589$
) produced the number of majority-minority districts using a neutral process. On the other hand, it is extremely unlikely that Virginia (
$p<0.0001$
) arrived at two majority-minority districts by way of a neutral process.Footnote
27
5 Possible Extensions
The algorithm we propose in this article neutrally generates a set of districts without indication of bias that are contiguous, balanced, and relatively compact; however, analysts may wish to apply additional constraints to the process of drawing legislative districts. For example, some jurisdictions seek to keep whole existing political units like municipalities or counties. In addition, mapmakers may seek to generate a particular number of majority-minority districts. While we forgo the imposition of additional constraints in this article, it is worth noting briefly that, with modification, the graph partitioning approach we propose could incorporate additional constraints.
Applying additional constraints to the sample drawn by the algorithm requires; first, that we allow for heterogeneity in the relationship between geographic units. Recall, we weighted geographic units (vertices) according to the number of people that reside in the unit. In the analysis we present here, all the relationships between units (edges) are weighted equally, but that need not be so. Our approach could be altered to weigh the relationship between units, and those weights could vary according to any number of factors of interest. For instance, we might apply higher weights to edges between vertices that should fall in the same district (e.g. units in the same municipality). Likewise, we could apply a lower weight to edges between units that need not fall in the same district (units not in the same municipality).
Second, we could alter the algorithm to minimize the weight of edges it cuts to create districts. Fortunately, there already exist a host of graph partitioning algorithms developed by computer scientists that minimize the edge cut while maintaining the balance in the weight applied to vertices across partitions (for example, see Karypis and Kumar Reference Karypis and Kumar1995, Reference Karypis and Kumar1998). These algorithms could be modified to address the problem of dividing geographic units into legislative districts. Using this approach, we have begun the process of incorporating additional constraints into studies of the impact of maintaining communities of interest (the practice of keeping cities and counties whole in legislative maps) and majority-minority districts on legislative districts and policy outcomes.
6 Conclusion
In this article, we have proposed a computationally efficient algorithm that generates a set of districts that are contiguous, balanced, relatively compact, and which do not show the kinds of biases found in previous algorithms. We base our algorithm on one proposed by computer scientists to divide tasks weighted by computational complexity evenly between processors. In our application of the algorithm, geographic units are analogous to tasks and the population of the geographic units are the weights. The algorithm gains efficiency by first simplifying a map into a much simpler graph, partitioning the simpler version of the graph, and then projecting that partition back into the complex version of the map. In the last step of the process we apply the Kernighan–Lin algorithm, used by computer scientists to refine assignments of computational tasks to a computer’s processor, to attain districts that are more balanced in terms of population.
As a demonstration of the algorithm’s capabilities, we compare an approximate distribution of neutral districts to the actual congressional districts in Mississippi, Virginia, and Texas produced in the round of redistricting following the 2010 census. The algorithm generated 10,000 valid and distinct maps consisting of balanced and contiguous districts, from computationally intensive block-level data for each state. The patterns of minority concentration we observe in each of these states are inconsistent with patterns that might have arisen through a neutral process. In other words, what we observe appears to be a deliberate attempt by mapmakers in Mississippi, Virginia, and Texas to generate majority-minority seats. Absent such an effort, we would expect a set of districts in each state that would make it challenging for minority voters to select a candidate of their choosing.
The concentration of minority voters almost certainly reverberates through the politics of each of these states. In particular, by concentrating minority voters, who tend to support Democratic candidates, into a few districts, mapmakers also concentrate Democratic voters into a few districts. The consequence is that the remaining districts are almost certainly more Republican than we would expect if the process of redistricting followed more neutral patterns. We forgo an analysis of the partisan implications of these patterns of redistricting here, but we acknowledge that the method we have presented may be usefully applied in the evaluation of potential racial or partisan gerrymanders.
The purpose of this article is to demonstrate a method for drawing neutral legislative districts that is an advance over prior published algorithms; however, the analysis we present here allows us to make substantive conclusions about legislative districts in Mississippi, Virginia, and Texas. Our conclusions suggest at least two avenues of further research. First, we may explore the extent to which the inclusion of majority-minority districts allows for minority representation in other states. Determining the extent of packing in other jurisdictions would require analyzing more states than space permits in this article. Since our algorithm handles even the largest jurisdictions using the most complex data, analyzing any other jurisdictions would not be problematic. Second, we can use the algorithm to characterize the distribution of partisan voters in a null distribution. The null distribution retrieved by the algorithm also serves as a counterfactual against which we can compare patterns of partisanship in enacted maps. We intend to pursue questions related to the broader practice and implications of racial and partisan gerrymandering in future work.
Appendix A. Formal Presentation of Algorithm
Step 1 (“Coarsening”)
We transform
$G_{0}$
into a series of smaller graphs
$G_{1},G_{2},G_{3},\ldots ,G_{m}$
where
$|A_{0}|>|A_{1}|>|A_{2}|>|A_{3}|>\cdots >|A_{m}|$
. The algorithm selects a vertex
$u\in A_{i}$
with probability
$1/n_{i}$
where
$n_{i}=|A_{i}|$
. If
$u$
has not been selected previously, then the algorithm matches
$u$
with
$v\in V_{i}^{u}$
with probability
$1/|V_{i}^{u}|$
where
$V_{i}^{u}$
is the set of unmatched vertices adjacent to
$u$
. If
$\exists \;v\in V_{i}^{u}$
, then the algorithm collapses
$u$
and
$v$
into a multinode
$a_{j}\in A_{i+1}$
. In
$G_{i+1}$
, the weight of the multinode,
$w(a_{j})=w(u)+w(v)$
, and
$E_{a_{j}}=E_{u}\cup E_{v}$
. If
$V_{i}^{u}=\emptyset$
, then
$u$
remains unmatched. Unmatched vertices are copied over to
$G_{i+1}$
.
Step 2 (“Partitioning”)
We compute a
$k$
-way partition
$P_{m}$
of graph
$G_{m}$
that divides
$V_{m}$
into
$k$
parts each containing
$|A_{m}|/k$
vertices. The algorithm chooses a multinode
$A_{i}\in A_{m}$
with probability
$1/|A_{m}|$
. It then chooses another block
$u\in V_{i}^{A_{i}}$
with probability
$1/|V_{i}^{A_{i}}|$
and combines the multinode into a district
$P_{m}[v]$
. If
$w(u)+w(A_{i})\geqslant 1/kW(A_{m})$
or
$w(u)+w(P_{m}[v])\geqslant 1/kW(A_{m})$
, the algorithm stops adding multinodes to the district. If
$w(u)+w(A_{i})<1/2W(A_{m})$
or
$w(u)+w(P_{m}[v])<1/2W(A_{m})$
, then the algorithm repeats step 2; however, it chooses
$u\in V_{i}^{P_{m}[v]}$
in every iteration after the first.
Step 3 (“Uncoarsening”)
By going through a set of intermediate partitions
$P_{m-1},P_{m-2},\ldots ,P_{1},P_{0}$
, the algorithm projects
$P_{m}$
of
$G_{m}$
back onto
$G_{0}$
. At every step of the uncoarsening process, the algorithm assigns
$P_{i}[u]=P_{i+1}[v],\;\forall \;v\in V_{i}^{u}$
.
Step 4 (“Refinement”)
Consider a partition that has two parts
$v$
and
$u$
. For each
$P_{m-1},P_{m-1},\ldots ,P_{0}$
in the uncoarsening step, let
$v$
and
$u$
be two parts of
$P_{i}$
. The algorithm selects
$v_{i+1}^{\prime }\subset v_{i+1}$
and
$u_{i+1}^{\prime }\subset u_{i+1}$
where
$v_{i+1}^{\prime }$
is contiguous with
$u_{i+1}$
and
$u_{i+1}^{\prime }$
is contiguous with
$v_{i+1}$
. If
$|w(v_{i+1})-w(u_{i+1})|>|w(v_{i+1}\setminus v_{i+1}^{\prime }\cup u_{i+1}^{\prime })-w(u_{i+1}\setminus u_{i+1}^{\prime }\cup v_{i+1}^{\prime })|$
then it sets
$v_{i}=v_{i+1}\setminus v_{i+1}^{\prime }\cup u_{i+1}^{\prime }$
and
$u_{i}=u_{i+1}\setminus u_{i+1}^{\prime }\cup v_{i+1}^{\prime }$
, otherwise
$v_{i}=v_{i+1}$
and
$u_{i}=u_{i+1}$
.
Step 5 (“Repeat”)
If the resulting partition is a set of contiguous and balanced districts, we record the partition for later analysis. If not, the flawed partition is discarded and the algorithm restarts.
Appendix B. Algorithmic Complexity
B.1 Our proposed algorithm
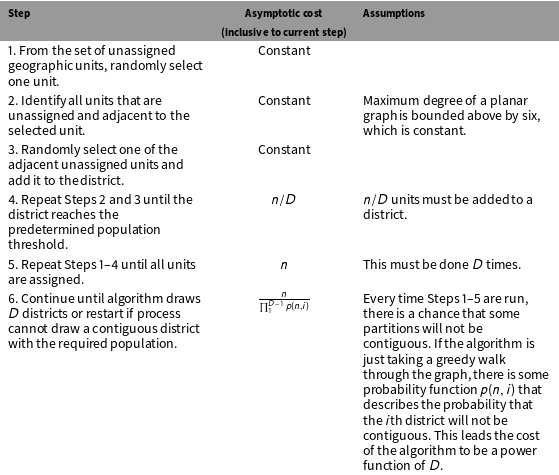
Table B1. Asymptotic cost of our proposed algorithm.
B.2 Cirincione, Darling, and O’Rourke (2000)
Table B2. Asymptotic Cost of Cirincione, Darling, and O’Rourke (2000).
