1 Introduction
Difference-in-differences (DID) is one of the most commonly used empirical designs in today’s social sciences. The identifying assumptions for DID include the “parallel trends” assumption, which states that in the absence of the treatment the average outcomes of treated and control units would have followed parallel paths. This assumption is not directly testable, but researchers have more confidence in its validity when they find that the average outcomes of the treated and control units follow parallel paths in pretreatment periods. In many cases, however, parallel pretreatment trends are not supported by data, a clear sign that the “parallel trends” assumption is likely to fail in the posttreatment period as well. This paper attempts to deal with this problem systematically. It proposes a method that estimates the average treatment effect on the treated using time-series cross-sectional (TSCS) data when the “parallel trends” assumption is not likely to hold.
The presence of unobserved time-varying confounders causes the failure of this assumption. There are broadly two approaches in the literature to deal with this problem. The first one is to condition on pretreatment observables using matching methods, which may help balance the influence of potential time-varying confounders between treatment and control groups. For example, Abadie (Reference Abadie2005) proposes matching before DID estimations. Although this method is easy to implement, it does not guarantee parallel pretreatment trends. The synthetic control method proposed by Abadie, Diamond, and Hainmueller (Reference Abadie, Diamond and Hainmueller2010, Reference Abadie, Diamond and Hainmueller2015) goes one step further. It matches both pretreatment covariates and outcomes between a treated unit and a set of control units and uses pretreatment periods as criteria for good matches.Footnote 1 Specifically, it constructs a “synthetic control unit” as the counterfactual for the treated unit by reweighting the control units. It provides explicit weights for the control units, thus making the comparison between the treated and synthetic control units transparent. However, it only applies to the case of one treated unit and the uncertainty estimates it offers are not easily interpretable.Footnote 2
The second approach is to model the unobserved time-varying heterogeneities explicitly. A widely used strategy is to add in unit-specific linear or quadratic time trends to conventional two-way fixed effects models. By doing so, researchers essentially rely upon a set of alternative identification assumptions that treatment assignment is ignorable conditional on both the fixed effects and the imposed trends (Mora and Reggio Reference Mora and Reggio2012). Controlling for these trends, however, often consumes a large number of degrees of freedom and may not necessarily solve the problem if the underlying confounders are not in forms of the specified trends.
An alternative way is to model unobserved time-varying confounders semiparametrically. For example, Bai (Reference Bai2009) proposes an interactive fixed effects (IFE) model, which incorporates unit-specific intercepts interacted with time-varying coefficients. The time-varying coefficients are also referred to as (latent) factors while the unit-specific intercepts are labeled as factor loadings. This approach builds upon an earlier literature on factor models in quantitative finance.Footnote 3 The model is estimated by iteratively conducting a factor analysis of the residuals from a linear model and estimating the linear model that takes into account the influences of a fixed number of most influential factors. Pang (Reference Pang2010, Reference Pang2014) explores nonlinear IFE models with exogenous covariates in a Bayesian multi-level framework. Stewart (Reference Stewart2014) provides a general framework of estimating IFE models based on a Bayesian variational inference algorithm. Gobillon and Magnac (Reference Gobillon and Magnac2016) show that IFE models outperform the synthetic control method in DID settings when factor loadings of the treatment and control groups do not share common support.Footnote 4
This paper proposes a generalized synthetic control (GSC) method that links the two approaches and unifies the synthetic control method with linear fixed effects models under a simple framework, of which DID is a special case. It first estimates an IFE model using only the control group data, obtaining a fixed number of latent factors. It then estimates factor loadings for each treated unit by linearly projecting pretreatment treated outcomes onto the space spanned by these factors. Finally, it imputes treated counterfactuals based on the estimated factors and factor loadings. The main contribution of this paper, hence, is to employ a latent factor approach to address a causal inference problem and provide valid, simulation-based uncertainty estimates under reasonable assumptions.
This method is in the spirit of the synthetic control method in the sense that by essence it is a reweighting scheme that takes pretreatment treated outcomes as benchmarks when choosing weights for control units and uses cross-sectional correlations between treated and control units to predict treated counterfactuals. Unlike the synthetic matching method, however, it conducts dimension reduction prior to reweighting such that vectors to be reweighted on are smoothed across control units. The method can also be understood as a bias correction procedure for IFE models when the treatment effect is heterogeneous across units.Footnote 5 It treats counterfactuals of treated units as missing data and makes out-of-sample predictions for posttreatment treated outcomes based on an IFE model.
This method has several advantages. First, it generalizes the synthetic control method to cases of multiple treated units and/or variable treatment periods. Since the IFE model is estimated only once, treated counterfactuals are obtained in a single run. Users therefore no longer need to find matches of control units for each treated unit one by one.Footnote 6 This makes the algorithm fast and less sensitive to the idiosyncrasies of a small number of observations.
Second, the GSC method produces frequentist uncertainty estimates, such as standard errors and confidence intervals, and improves efficiency under correct model specifications. A parametric bootstrap procedure based on simulated data can provide valid inference under reasonable assumptions. Since no observations are discarded from the control group, this method uses more information from the control group and thus is more efficient than the synthetic matching method when the model is correctly specified.
Third, it embeds a cross-validation scheme that selects the number of factors of the IFE model automatically, and thus is easy to implement. One advantage of the DID data structure is that treated observations in pretreatment periods can naturally serve as a validation dataset for model selection. We show that with sufficient data, the cross-validation procedure can pick up the correct number of factors with high probability, therefore reducing the risks of overfitting.
The GSC method has two main limitations. First, it requires more pretreatment data than fixed effects estimators. When the number of pretreatment periods is small, “incidental parameters” can lead to biased estimates of the treatment effects. Second, and perhaps more importantly, modeling assumptions play a heavier role with the GSC method than the original synthetic matching method. For example, if the treated and control units do not share common support in factor loadings, the synthetic matching method may simply fail to construct a synthetic control unit. Since such a problem is obvious to users, the chances that users misuse the method are small. The GSC method, however, will still impute treated counterfactuals based on model extrapolation, which may lead to erroneous conclusions. To safeguard against this risk, it is crucial to conduct various diagnostic checks, such as plotting the raw data, fitted values, and predicted counterfactuals.
The rest of the paper is organized as follows. Section 2 sets up the model and defines the quantities of interest. Section 3 introduces the GSC estimator, describes how it is implemented, and discuss the parametric bootstrap procedure. Section 4 reports simulation results that explores the finite sample properties of the GSC estimator and compares it with several existing methods. Section 5 illustrates the method with an empirical example that investigates the effect of Election Day Registration (EDR) laws on voter turnout in the United States. The last section concludes.
2 Framework
Suppose
![]() $Y_{it}$
is the outcome of interest of unit
$Y_{it}$
is the outcome of interest of unit
![]() $i$
at time
$i$
at time
![]() $t$
. Let
$t$
. Let
![]() ${\mathcal{T}}$
and
${\mathcal{T}}$
and
![]() ${\mathcal{C}}$
denote the sets of units in treatment and control groups, respectively. The total number of units is
${\mathcal{C}}$
denote the sets of units in treatment and control groups, respectively. The total number of units is
![]() $N=N_{tr}+N_{co}$
, where
$N=N_{tr}+N_{co}$
, where
![]() $N_{tr}$
and
$N_{tr}$
and
![]() $N_{co}$
are the numbers of treated and control units, respectively. All units are observed for
$N_{co}$
are the numbers of treated and control units, respectively. All units are observed for
![]() $T$
periods (from time
$T$
periods (from time
![]() $1$
to time
$1$
to time
![]() $T$
). Let
$T$
). Let
![]() $T_{0,i}$
be the number of pretreatment periods for unit
$T_{0,i}$
be the number of pretreatment periods for unit
![]() $i$
, which is first exposed to the treatment at time
$i$
, which is first exposed to the treatment at time
![]() $(T_{0,i}+1)$
and subsequently observed for
$(T_{0,i}+1)$
and subsequently observed for
![]() $q_{i}=T-T_{0,i}$
periods. Units in the control group are never exposed to the treatment in the observed time span. For notational convenience, we assume that all treated units are first exposed to the treatment at the same time, i.e.,
$q_{i}=T-T_{0,i}$
periods. Units in the control group are never exposed to the treatment in the observed time span. For notational convenience, we assume that all treated units are first exposed to the treatment at the same time, i.e.,
![]() $T_{0,i}=T_{0}$
and
$T_{0,i}=T_{0}$
and
![]() $q_{i}=q$
; variable treatment periods can be easily accommodated. First, we assume that
$q_{i}=q$
; variable treatment periods can be easily accommodated. First, we assume that
![]() $Y_{it}$
is given by a linear factor model.
$Y_{it}$
is given by a linear factor model.
Assumption 1. Functional form:
where the treatment indicator
![]() $D_{it}$
equals 1 if unit
$D_{it}$
equals 1 if unit
![]() $i$
has been exposed to the treatment prior to time
$i$
has been exposed to the treatment prior to time
![]() $t$
and equals 0 otherwise (i.e.,
$t$
and equals 0 otherwise (i.e.,
![]() $D_{it}=1$
when
$D_{it}=1$
when
![]() $i\in {\mathcal{T}}$
and
$i\in {\mathcal{T}}$
and
![]() $t>T_{0}$
and
$t>T_{0}$
and
![]() $D_{it}=0$
otherwise).Footnote
7
$D_{it}=0$
otherwise).Footnote
7
![]() $\unicode[STIX]{x1D6FF}_{it}$
is the heterogeneous treatment effect on unit
$\unicode[STIX]{x1D6FF}_{it}$
is the heterogeneous treatment effect on unit
![]() $i$
at time
$i$
at time
![]() $t$
;
$t$
;
![]() $x_{it}$
is a
$x_{it}$
is a
![]() $(k\times 1)$
vector of observed covariates,
$(k\times 1)$
vector of observed covariates,
![]() $\unicode[STIX]{x1D6FD}=[\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{k}]^{\prime }$
is a
$\unicode[STIX]{x1D6FD}=[\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{k}]^{\prime }$
is a
![]() $(k\times 1)$
vector of unknown parameters,Footnote
8
$(k\times 1)$
vector of unknown parameters,Footnote
8
![]() $f_{t}=[f_{1t},\ldots ,f_{rt}]^{\prime }$
is an
$f_{t}=[f_{1t},\ldots ,f_{rt}]^{\prime }$
is an
![]() $(r\times 1)$
vector of unobserved common factors,
$(r\times 1)$
vector of unobserved common factors,
![]() $\unicode[STIX]{x1D706}_{i}=[\unicode[STIX]{x1D706}_{i1},\ldots ,\unicode[STIX]{x1D706}_{ir}]^{\prime }$
is an
$\unicode[STIX]{x1D706}_{i}=[\unicode[STIX]{x1D706}_{i1},\ldots ,\unicode[STIX]{x1D706}_{ir}]^{\prime }$
is an
![]() $(r\times 1)$
vector of unknown factor loadings, and
$(r\times 1)$
vector of unknown factor loadings, and
![]() $\unicode[STIX]{x1D700}_{it}$
represents unobserved idiosyncratic shocks for unit
$\unicode[STIX]{x1D700}_{it}$
represents unobserved idiosyncratic shocks for unit
![]() $i$
at time
$i$
at time
![]() $t$
and has zero mean. Assumption 1 requires that the treated and control units are affected by the same set of factors and the number of factors is fixed during the observed time periods, i.e., no structural breaks are allowed.
$t$
and has zero mean. Assumption 1 requires that the treated and control units are affected by the same set of factors and the number of factors is fixed during the observed time periods, i.e., no structural breaks are allowed.
The factor component of the model,
![]() $\unicode[STIX]{x1D706}_{i}^{\prime }f_{t}=\unicode[STIX]{x1D706}_{i1}f_{1t}+\unicode[STIX]{x1D706}_{i2}f_{2t}+\cdots +\unicode[STIX]{x1D706}_{ir}f_{rt}$
, takes a linear, additive form by assumption. In spite of the seemingly restrictive form, it covers a wide range of unobserved heterogeneities. First and foremost, conventional additive unit and time fixed effects are special cases. To see this, if we set
$\unicode[STIX]{x1D706}_{i}^{\prime }f_{t}=\unicode[STIX]{x1D706}_{i1}f_{1t}+\unicode[STIX]{x1D706}_{i2}f_{2t}+\cdots +\unicode[STIX]{x1D706}_{ir}f_{rt}$
, takes a linear, additive form by assumption. In spite of the seemingly restrictive form, it covers a wide range of unobserved heterogeneities. First and foremost, conventional additive unit and time fixed effects are special cases. To see this, if we set
![]() $f_{1t}=1$
and
$f_{1t}=1$
and
![]() $\unicode[STIX]{x1D706}_{i2}=1$
and rewrite
$\unicode[STIX]{x1D706}_{i2}=1$
and rewrite
![]() $\unicode[STIX]{x1D706}_{i1}=\unicode[STIX]{x1D6FC}_{i}$
and
$\unicode[STIX]{x1D706}_{i1}=\unicode[STIX]{x1D6FC}_{i}$
and
![]() $f_{2t}=\unicode[STIX]{x1D709}_{t}$
, then
$f_{2t}=\unicode[STIX]{x1D709}_{t}$
, then
![]() $\unicode[STIX]{x1D706}_{i1}f_{1t}+\unicode[STIX]{x1D706}_{i2}f_{2t}=\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D709}_{t}$
.Footnote
9
Moreover, the term also incorporates cases ranging from unit-specific linear or quadratic time trends to autoregressive components that researchers often control for when analyzing TSCS data.Footnote
10
In general, as long as an unobserved random variable can be decomposed into a multiplicative form, i.e.,
$\unicode[STIX]{x1D706}_{i1}f_{1t}+\unicode[STIX]{x1D706}_{i2}f_{2t}=\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D709}_{t}$
.Footnote
9
Moreover, the term also incorporates cases ranging from unit-specific linear or quadratic time trends to autoregressive components that researchers often control for when analyzing TSCS data.Footnote
10
In general, as long as an unobserved random variable can be decomposed into a multiplicative form, i.e.,
![]() $U_{it}=a_{i}\times b_{t}$
, it can be absorbed by
$U_{it}=a_{i}\times b_{t}$
, it can be absorbed by
![]() $\unicode[STIX]{x1D706}_{i}^{\prime }f_{t}$
while it cannot capture unobserved confounders that are independent across units.
$\unicode[STIX]{x1D706}_{i}^{\prime }f_{t}$
while it cannot capture unobserved confounders that are independent across units.
To formalize the notion of causality, we also use the notation from the potential outcomes framework for causal inference (Neyman Reference Neyman1923; Rubin Reference Rubin1974; Holland Reference Holland1986). Let
![]() $Y_{it}(1)$
and
$Y_{it}(1)$
and
![]() $Y_{it}(0)$
be the potential outcomes for individual
$Y_{it}(0)$
be the potential outcomes for individual
![]() $i$
at time
$i$
at time
![]() $t$
when
$t$
when
![]() $D_{it}=1$
or
$D_{it}=1$
or
![]() $D_{it}=0$
, respectively. We thus have
$D_{it}=0$
, respectively. We thus have
![]() $Y_{it}(0)=x_{it}^{\prime }\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D706}_{i}^{\prime }f_{t}+\unicode[STIX]{x1D700}_{it}$
and
$Y_{it}(0)=x_{it}^{\prime }\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D706}_{i}^{\prime }f_{t}+\unicode[STIX]{x1D700}_{it}$
and
![]() $Y_{it}(1)=\unicode[STIX]{x1D6FF}_{it}+x_{it}^{\prime }\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D706}_{i}^{\prime }f_{t}+\unicode[STIX]{x1D700}_{it}$
. The individual treatment effect on treated unit
$Y_{it}(1)=\unicode[STIX]{x1D6FF}_{it}+x_{it}^{\prime }\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D706}_{i}^{\prime }f_{t}+\unicode[STIX]{x1D700}_{it}$
. The individual treatment effect on treated unit
![]() $i$
at time
$i$
at time
![]() $t$
is therefore
$t$
is therefore
![]() $\unicode[STIX]{x1D6FF}_{it}=Y_{it}(1)-Y_{it}(0)$
for any
$\unicode[STIX]{x1D6FF}_{it}=Y_{it}(1)-Y_{it}(0)$
for any
![]() $i\in {\mathcal{T}}$
,
$i\in {\mathcal{T}}$
,
![]() $t>T_{0}$
.
$t>T_{0}$
.
We can rewrite the DGP of each unit as:
where
![]() $Y_{i}=[Y_{i1},Y_{i2},\ldots ,Y_{iT}]^{\prime }$
;
$Y_{i}=[Y_{i1},Y_{i2},\ldots ,Y_{iT}]^{\prime }$
;
![]() $D_{i}=[D_{i1},D_{i2},\ldots ,D_{iT}]^{\prime }$
and
$D_{i}=[D_{i1},D_{i2},\ldots ,D_{iT}]^{\prime }$
and
![]() $\unicode[STIX]{x1D6FF}_{i}=[\unicode[STIX]{x1D6FF}_{i1},\unicode[STIX]{x1D6FF}_{i2},\ldots ,\unicode[STIX]{x1D6FF}_{iT}]^{\prime }$
(symbol “
$\unicode[STIX]{x1D6FF}_{i}=[\unicode[STIX]{x1D6FF}_{i1},\unicode[STIX]{x1D6FF}_{i2},\ldots ,\unicode[STIX]{x1D6FF}_{iT}]^{\prime }$
(symbol “
![]() $\circ$
” stands for point-wise product);
$\circ$
” stands for point-wise product);
![]() $\unicode[STIX]{x1D700}_{i}=[\unicode[STIX]{x1D700}_{i1},\unicode[STIX]{x1D700}_{i2},\ldots ,\unicode[STIX]{x1D700}_{iT}]^{\prime }$
are
$\unicode[STIX]{x1D700}_{i}=[\unicode[STIX]{x1D700}_{i1},\unicode[STIX]{x1D700}_{i2},\ldots ,\unicode[STIX]{x1D700}_{iT}]^{\prime }$
are
![]() $(T\times 1)$
vectors;
$(T\times 1)$
vectors;
![]() $X_{i}=[x_{i1},x_{i2},\ldots ,x_{iT}]^{\prime }$
is a
$X_{i}=[x_{i1},x_{i2},\ldots ,x_{iT}]^{\prime }$
is a
![]() $(T\times k)$
matrix; and
$(T\times k)$
matrix; and
![]() $F=[f_{1},f_{2},\ldots ,f_{T}]^{\prime }$
is a
$F=[f_{1},f_{2},\ldots ,f_{T}]^{\prime }$
is a
![]() $(T\times r)$
matrix.
$(T\times r)$
matrix.
The control and treated units are subscripted from 1 to
![]() $N_{co}$
and from
$N_{co}$
and from
![]() $N_{co}+1$
to
$N_{co}+1$
to
![]() $N$
, respectively. The DGP of a control unit can be expressed as:
$N$
, respectively. The DGP of a control unit can be expressed as:
![]() $Y_{i}=X_{i}\unicode[STIX]{x1D6FD}+F\unicode[STIX]{x1D706}_{i}+\unicode[STIX]{x1D700}_{i}$
,
$Y_{i}=X_{i}\unicode[STIX]{x1D6FD}+F\unicode[STIX]{x1D706}_{i}+\unicode[STIX]{x1D700}_{i}$
,
![]() $i\in 1,2,\ldots N_{co}$
. Stacking all control units together, we have:
$i\in 1,2,\ldots N_{co}$
. Stacking all control units together, we have:
in which
![]() $Y_{co}=[Y_{1},Y_{2},\ldots ,Y_{N_{co}}]$
and
$Y_{co}=[Y_{1},Y_{2},\ldots ,Y_{N_{co}}]$
and
![]() $\unicode[STIX]{x1D700}_{co}=[\unicode[STIX]{x1D700}_{1},\unicode[STIX]{x1D700}_{2},\ldots ,\unicode[STIX]{x1D700}_{N_{co}}]$
are
$\unicode[STIX]{x1D700}_{co}=[\unicode[STIX]{x1D700}_{1},\unicode[STIX]{x1D700}_{2},\ldots ,\unicode[STIX]{x1D700}_{N_{co}}]$
are
![]() $(T\times N_{co})$
matrices;
$(T\times N_{co})$
matrices;
![]() $X_{co}$
is a three-dimensional
$X_{co}$
is a three-dimensional
![]() $(T\times N_{co}\times p)$
matrix; and
$(T\times N_{co}\times p)$
matrix; and
![]() $\unicode[STIX]{x1D6EC}_{co}=[\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2},\ldots ,\unicode[STIX]{x1D706}_{N_{co}}]^{\prime }$
is a
$\unicode[STIX]{x1D6EC}_{co}=[\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2},\ldots ,\unicode[STIX]{x1D706}_{N_{co}}]^{\prime }$
is a
![]() $(N_{co}\times r)$
matrix, hence, the products
$(N_{co}\times r)$
matrix, hence, the products
![]() $X_{co}\unicode[STIX]{x1D6FD}$
and
$X_{co}\unicode[STIX]{x1D6FD}$
and
![]() $F\unicode[STIX]{x1D6EC}_{co}^{\prime }$
are also
$F\unicode[STIX]{x1D6EC}_{co}^{\prime }$
are also
![]() $(T\times N_{co})$
matrices. To identify
$(T\times N_{co})$
matrices. To identify
![]() $\unicode[STIX]{x1D6FD}$
,
$\unicode[STIX]{x1D6FD}$
,
![]() $F$
and
$F$
and
![]() $\unicode[STIX]{x1D6EC}_{co}$
in Equation (1), more constraints are needed. Following Bai (Reference Bai2003, Reference Bai2009), I add two sets of constraints on the factors and factor loadings: (1) all factor are normalized, and (2) they are orthogonal to each other, i.e.:
$\unicode[STIX]{x1D6EC}_{co}$
in Equation (1), more constraints are needed. Following Bai (Reference Bai2003, Reference Bai2009), I add two sets of constraints on the factors and factor loadings: (1) all factor are normalized, and (2) they are orthogonal to each other, i.e.:
![]() $F^{\prime }F/T=I_{r}$
and
$F^{\prime }F/T=I_{r}$
and
![]() $\unicode[STIX]{x1D6EC}_{co}^{\prime }\unicode[STIX]{x1D6EC}_{co}=\text{diagonal}$
.Footnote
11
For the moment, the number of factors
$\unicode[STIX]{x1D6EC}_{co}^{\prime }\unicode[STIX]{x1D6EC}_{co}=\text{diagonal}$
.Footnote
11
For the moment, the number of factors
![]() $r$
is assumed to be known. In the next section, we propose a cross-validation procedure that automates the choice of
$r$
is assumed to be known. In the next section, we propose a cross-validation procedure that automates the choice of
![]() $r$
.
$r$
.
The main quantity of interest of this paper is the average treatment effect on the treated (ATT) at time
![]() $t$
(when
$t$
(when
![]() $t>T_{0}$
):
$t>T_{0}$
):
Note that in this paper, as in Abadie, Diamond, and Hainmueller (Reference Abadie, Diamond and Hainmueller2010), we treat the treatment effects
![]() $\unicode[STIX]{x1D6FF}_{it}$
as given once the sample is drawn.Footnote
13
Because
$\unicode[STIX]{x1D6FF}_{it}$
as given once the sample is drawn.Footnote
13
Because
![]() $Y_{it}(1)$
is observed for treated units in posttreatment periods, the main objective of this paper is to construct counterfactuals for each treated unit in posttreatment periods, i.e.,
$Y_{it}(1)$
is observed for treated units in posttreatment periods, the main objective of this paper is to construct counterfactuals for each treated unit in posttreatment periods, i.e.,
![]() $Y_{it}(0)$
for
$Y_{it}(0)$
for
![]() $i\in {\mathcal{T}}$
and
$i\in {\mathcal{T}}$
and
![]() $t>T_{0}$
. The problem of causal inference indeed turns into a problem of forecasting missing data.Footnote
14
$t>T_{0}$
. The problem of causal inference indeed turns into a problem of forecasting missing data.Footnote
14
2.1 Assumptions for causal identification
In addition to the functional form assumption (Assumption 1), three assumptions are required for the identification of the quantities of interest. Among them, the assumption of strict exogeneity is the most important.
Assumption 2. Strict exogeneity.
Assumption 2 means that the error term of any unit at any time period is independent of treatment assignment, observed covariates, and unobserved cross-sectional and temporal heterogeneities of all units (including itself) at all periods. We call it a strict exogeneity assumption, which implies conditional mean independence, i.e.,
![]() $\mathbb{E}[\unicode[STIX]{x1D700}_{it}|D_{it},x_{it},\unicode[STIX]{x1D706}_{i},f_{t}]=\mathbb{E}[\unicode[STIX]{x1D700}_{it}|x_{it},\unicode[STIX]{x1D706}_{i},f_{t}]=0$
.Footnote
15
$\mathbb{E}[\unicode[STIX]{x1D700}_{it}|D_{it},x_{it},\unicode[STIX]{x1D706}_{i},f_{t}]=\mathbb{E}[\unicode[STIX]{x1D700}_{it}|x_{it},\unicode[STIX]{x1D706}_{i},f_{t}]=0$
.Footnote
15
Assumption 2 is arguably weaker than the strict exogeneity assumption required by fixed effects models when decomposable time-varying confounders are at present. These confounders are decomposable if they can take forms of heterogeneous impacts of a common trend or a series of common shocks. For instance, suppose a law is passed in a state because the public opinion in that state becomes more liberal. Because changing ideologies are often cross-sectionally correlated across states, a latent factor may be able to capture shifting ideology at the national level; the national shifts may have a larger impact on a state that has a tradition of mass liberalism or has a higher proportion of manufacturing workers than a state that is historically conservative. Controlling for this unobserved confounder, therefore, can alleviate the concern that the passage of the law is endogenous to changing ideology of a state’s constituents to a great extent.
When such a confounder exists, with two-ways fixed effects models we need to assume that
![]() $(\unicode[STIX]{x1D700}_{it}+\unicode[STIX]{x1D706}_{i}f_{t})\bot \!\!\!\bot D_{js},x_{js},\unicode[STIX]{x1D6FC}_{j},\unicode[STIX]{x1D709}_{s},\forall i,j,t,s$
(with
$(\unicode[STIX]{x1D700}_{it}+\unicode[STIX]{x1D706}_{i}f_{t})\bot \!\!\!\bot D_{js},x_{js},\unicode[STIX]{x1D6FC}_{j},\unicode[STIX]{x1D709}_{s},\forall i,j,t,s$
(with
![]() $\unicode[STIX]{x1D706}_{i}f_{t}$
,
$\unicode[STIX]{x1D706}_{i}f_{t}$
,
![]() $\unicode[STIX]{x1D6FC}_{j}$
and
$\unicode[STIX]{x1D6FC}_{j}$
and
![]() $\unicode[STIX]{x1D709}_{s}$
representing the time-varying confounder for unit
$\unicode[STIX]{x1D709}_{s}$
representing the time-varying confounder for unit
![]() $i$
at time
$i$
at time
![]() $t$
, fixed effect for unit
$t$
, fixed effect for unit
![]() $j$
, and fixed effect for time
$j$
, and fixed effect for time
![]() $s$
, respectively) for the identification of the constant treatment effect. This is implausible because
$s$
, respectively) for the identification of the constant treatment effect. This is implausible because
![]() $\unicode[STIX]{x1D706}_{i}f_{t}$
is likely to be correlated with
$\unicode[STIX]{x1D706}_{i}f_{t}$
is likely to be correlated with
![]() $D_{it}$
,
$D_{it}$
,
![]() $x_{it}$
, and
$x_{it}$
, and
![]() $\unicode[STIX]{x1D6FC}_{i}$
, not to mention other terms. In contrast, Assumption 2 allows the treatment indicator to be correlated with both
$\unicode[STIX]{x1D6FC}_{i}$
, not to mention other terms. In contrast, Assumption 2 allows the treatment indicator to be correlated with both
![]() $x_{js}$
and
$x_{js}$
and
![]() $\unicode[STIX]{x1D706}_{j}^{\prime }f_{s}$
for any unit
$\unicode[STIX]{x1D706}_{j}^{\prime }f_{s}$
for any unit
![]() $j$
at any time periods
$j$
at any time periods
![]() $s$
(including
$s$
(including
![]() $i$
and
$i$
and
![]() $t$
themselves).
$t$
themselves).
Identifying the treatment effects also requires the following assumptions:
Assumption 3. Weak serial dependence of the error terms.
Assumption 4. Regularity conditions.
Assumptions 3 and 4 (see the Online Appendix in Supplementary Materials for details) are needed for the consistent estimation of
![]() $\unicode[STIX]{x1D6FD}$
and the space spanned by
$\unicode[STIX]{x1D6FD}$
and the space spanned by
![]() $F$
(or
$F$
(or
![]() $F^{\prime }F/T$
). Similar, though slightly weaker, assumptions are made in Bai (Reference Bai2009) and Moon and Weidner (Reference Moon and Weidner2015). Assumption 3 allows weak serial correlations but rules out strong serial dependence, such as unit root processes; errors of different units are uncorrelated. A sufficient condition for Assumption 3 to hold is that the error terms are not only independent of covariates, factors, and factor loadings, but also independent both across units and over time, which is assumed in Abadie, Diamond, and Hainmueller (Reference Abadie, Diamond and Hainmueller2010). Assumption 4 specifies moment conditions that ensure the convergence of the estimator.
$F^{\prime }F/T$
). Similar, though slightly weaker, assumptions are made in Bai (Reference Bai2009) and Moon and Weidner (Reference Moon and Weidner2015). Assumption 3 allows weak serial correlations but rules out strong serial dependence, such as unit root processes; errors of different units are uncorrelated. A sufficient condition for Assumption 3 to hold is that the error terms are not only independent of covariates, factors, and factor loadings, but also independent both across units and over time, which is assumed in Abadie, Diamond, and Hainmueller (Reference Abadie, Diamond and Hainmueller2010). Assumption 4 specifies moment conditions that ensure the convergence of the estimator.
For valid inference based on a block bootstrap procedure discussed in the next section, we also need Assumption 5 (see Online Appendix for details). Heteroscedasticity across time, however, is allowed.
Assumption 5. The error terms are cross-sectionally independent and homoscedastic.
Remark 1. Assumptions 3 and 5 suggest that the error terms
![]() $\unicode[STIX]{x1D700}_{it}$
can be serially correlated. Assumption 2 rules out dynamic models with lagged dependent variables; however, this is mainly for the purpose of simplifying proofs (Bai Reference Bai2009, p. 1243). The proposed method can accommodate dynamic models as long as the error terms are not serially correlated.
$\unicode[STIX]{x1D700}_{it}$
can be serially correlated. Assumption 2 rules out dynamic models with lagged dependent variables; however, this is mainly for the purpose of simplifying proofs (Bai Reference Bai2009, p. 1243). The proposed method can accommodate dynamic models as long as the error terms are not serially correlated.
3 Estimation Strategy
In this section, we first propose a GSC estimator for treatment effect of each treated unit. It is essentially an out-of-sample prediction method based on Bai (Reference Bai2009)’s factor augmented model.
The GSC estimator for the treatment effect on treated unit
![]() $i$
at time
$i$
at time
![]() $t$
is given by the difference between the actual outcome and its estimated counterfactual:
$t$
is given by the difference between the actual outcome and its estimated counterfactual:
![]() $\hat{\unicode[STIX]{x1D6FF}}_{it}=Y_{it}(1)-{\hat{Y}}_{it}(0)$
, in which
$\hat{\unicode[STIX]{x1D6FF}}_{it}=Y_{it}(1)-{\hat{Y}}_{it}(0)$
, in which
![]() ${\hat{Y}}_{it}(0)$
is imputed with three steps. In the first step, we estimate an IFE model using only the control group data and obtain
${\hat{Y}}_{it}(0)$
is imputed with three steps. In the first step, we estimate an IFE model using only the control group data and obtain
![]() $\hat{\unicode[STIX]{x1D6FD}},\hat{F},\hat{\unicode[STIX]{x1D6EC}}_{co}$
:
$\hat{\unicode[STIX]{x1D6FD}},\hat{F},\hat{\unicode[STIX]{x1D6EC}}_{co}$
:
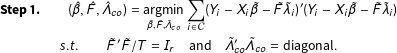 $$\begin{eqnarray}\displaystyle & \displaystyle \mathbf{Step1.}\qquad (\hat{\unicode[STIX]{x1D6FD}},\hat{F},\hat{\unicode[STIX]{x1D6EC}}_{co})=\underset{\tilde{\unicode[STIX]{x1D6FD}},\tilde{F},\tilde{\unicode[STIX]{x1D6EC}}_{co}}{\operatorname{argmin}}\mathop{\sum }_{i\in {\mathcal{C}}}(Y_{i}-X_{i}\tilde{\unicode[STIX]{x1D6FD}}-\tilde{F}\tilde{\unicode[STIX]{x1D706}}_{i})^{\prime }(Y_{i}-X_{i}\tilde{\unicode[STIX]{x1D6FD}}-\tilde{F}\tilde{\unicode[STIX]{x1D706}}_{i}) & \displaystyle \nonumber\\ \displaystyle & \mathit{s.t.}\qquad \tilde{F}^{\prime }\tilde{F}/T=I_{r}\quad \text{and}\quad \tilde{\unicode[STIX]{x1D6EC}}_{co}^{\prime }\tilde{\unicode[STIX]{x1D6EC}}_{co}=\text{diagonal}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \mathbf{Step1.}\qquad (\hat{\unicode[STIX]{x1D6FD}},\hat{F},\hat{\unicode[STIX]{x1D6EC}}_{co})=\underset{\tilde{\unicode[STIX]{x1D6FD}},\tilde{F},\tilde{\unicode[STIX]{x1D6EC}}_{co}}{\operatorname{argmin}}\mathop{\sum }_{i\in {\mathcal{C}}}(Y_{i}-X_{i}\tilde{\unicode[STIX]{x1D6FD}}-\tilde{F}\tilde{\unicode[STIX]{x1D706}}_{i})^{\prime }(Y_{i}-X_{i}\tilde{\unicode[STIX]{x1D6FD}}-\tilde{F}\tilde{\unicode[STIX]{x1D706}}_{i}) & \displaystyle \nonumber\\ \displaystyle & \mathit{s.t.}\qquad \tilde{F}^{\prime }\tilde{F}/T=I_{r}\quad \text{and}\quad \tilde{\unicode[STIX]{x1D6EC}}_{co}^{\prime }\tilde{\unicode[STIX]{x1D6EC}}_{co}=\text{diagonal}. & \displaystyle \nonumber\end{eqnarray}$$
We explain in detail how to estimate this model in the Online Appendix. The second step estimates factor loadings for each treated unit by minimizing the mean squared error of the predicted treated outcome in pretreatment periods:
 $$\begin{eqnarray}\displaystyle \mathbf{Step2.}\qquad \hat{\unicode[STIX]{x1D706}}_{i} & = & \displaystyle \underset{\tilde{\unicode[STIX]{x1D706}}_{i}}{\operatorname{argmin}}(Y_{i}^{0}-X_{i}^{0}\hat{\unicode[STIX]{x1D6FD}}-\hat{F^{0}}\tilde{\unicode[STIX]{x1D706}}_{i})^{\prime }(Y_{i}^{0}-X_{i}^{0}\hat{\unicode[STIX]{x1D6FD}}-\hat{F^{0}}\tilde{\unicode[STIX]{x1D706}}_{i})\nonumber\\ \displaystyle & = & \displaystyle (\hat{F}^{0\prime }\hat{F}^{0})^{-1}\hat{F}^{0\prime }(Y_{i}^{0}-X_{i}^{0}\hat{\unicode[STIX]{x1D6FD}}),\quad i\in {\mathcal{T}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbf{Step2.}\qquad \hat{\unicode[STIX]{x1D706}}_{i} & = & \displaystyle \underset{\tilde{\unicode[STIX]{x1D706}}_{i}}{\operatorname{argmin}}(Y_{i}^{0}-X_{i}^{0}\hat{\unicode[STIX]{x1D6FD}}-\hat{F^{0}}\tilde{\unicode[STIX]{x1D706}}_{i})^{\prime }(Y_{i}^{0}-X_{i}^{0}\hat{\unicode[STIX]{x1D6FD}}-\hat{F^{0}}\tilde{\unicode[STIX]{x1D706}}_{i})\nonumber\\ \displaystyle & = & \displaystyle (\hat{F}^{0\prime }\hat{F}^{0})^{-1}\hat{F}^{0\prime }(Y_{i}^{0}-X_{i}^{0}\hat{\unicode[STIX]{x1D6FD}}),\quad i\in {\mathcal{T}},\nonumber\end{eqnarray}$$
in which
![]() $\hat{\unicode[STIX]{x1D6FD}}$
and
$\hat{\unicode[STIX]{x1D6FD}}$
and
![]() $\hat{F}^{0}$
are from the first-step estimation and the superscripts “0”s denote the pretreatment periods. In the third step, we calculate treated counterfactuals based on
$\hat{F}^{0}$
are from the first-step estimation and the superscripts “0”s denote the pretreatment periods. In the third step, we calculate treated counterfactuals based on
![]() $\hat{\unicode[STIX]{x1D6FD}}$
,
$\hat{\unicode[STIX]{x1D6FD}}$
,
![]() $\hat{F}$
, and
$\hat{F}$
, and
![]() $\hat{\unicode[STIX]{x1D706}}_{i}$
:
$\hat{\unicode[STIX]{x1D706}}_{i}$
:
An estimator for
![]() $ATT_{t}$
therefore is:
$ATT_{t}$
therefore is:
![]() $\widehat{ATT}_{t}=(1/N_{tr})\sum _{i\in {\mathcal{T}}}[Y_{it}(1)-{\hat{Y}}_{it}(0)]$
for
$\widehat{ATT}_{t}=(1/N_{tr})\sum _{i\in {\mathcal{T}}}[Y_{it}(1)-{\hat{Y}}_{it}(0)]$
for
![]() $t>T_{0}$
.
$t>T_{0}$
.
Remark 2. In the Online Appendix, we show that, under Assumptions 1–4, the bias of the GSC shrinks to zero as the sample size grows, i.e.,
![]() $\mathbb{E}_{\unicode[STIX]{x1D700}}(\widehat{ATT}_{t}|D,X,\unicode[STIX]{x1D6EC},F)\rightarrow ATT_{t}$
as
$\mathbb{E}_{\unicode[STIX]{x1D700}}(\widehat{ATT}_{t}|D,X,\unicode[STIX]{x1D6EC},F)\rightarrow ATT_{t}$
as
![]() $N_{co},T_{0}\rightarrow 0$
(
$N_{co},T_{0}\rightarrow 0$
(
![]() $N_{tr}$
is taken as given), in which
$N_{tr}$
is taken as given), in which
![]() $D=[D_{1},D_{2},\ldots ,D_{N}]$
is a
$D=[D_{1},D_{2},\ldots ,D_{N}]$
is a
![]() $(T\times N)$
matrix,
$(T\times N)$
matrix,
![]() $X$
is a three-dimensional
$X$
is a three-dimensional
![]() $(T\times N\times p)$
matrix; and
$(T\times N\times p)$
matrix; and
![]() $\unicode[STIX]{x1D6EC}=[\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2},\ldots ,\unicode[STIX]{x1D706}_{N}]^{\prime }$
is a
$\unicode[STIX]{x1D6EC}=[\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2},\ldots ,\unicode[STIX]{x1D706}_{N}]^{\prime }$
is a
![]() $(N\times r)$
matrix. Intuitively, both large
$(N\times r)$
matrix. Intuitively, both large
![]() $N_{co}$
and large
$N_{co}$
and large
![]() $T_{0}$
are necessary for the convergences of
$T_{0}$
are necessary for the convergences of
![]() $\hat{\unicode[STIX]{x1D6FD}}$
and the estimated factor space. When
$\hat{\unicode[STIX]{x1D6FD}}$
and the estimated factor space. When
![]() $T_{0}$
is small, imprecise estimation of the factor loadings, or the “incidental parameters” problem, will lead to bias in the estimated treatment effects. This is a crucial difference from the conventional linear fixed effects models.
$T_{0}$
is small, imprecise estimation of the factor loadings, or the “incidental parameters” problem, will lead to bias in the estimated treatment effects. This is a crucial difference from the conventional linear fixed effects models.
3.1 Model selection
In practice, researchers may have limited knowledge of the exact number of factors to be included in the model. Therefore, we develop a cross-validation procedure to select models before estimating the causal effect. It relies on the control group information as well as information from the treatment group in pretreatment periods. Algorithm 1 describes the details of this procedure.
Algorithm 1 (Cross-validating the number of factors).
A leave-one-out-cross-validation procedure that selects the number of factors takes the following steps:

The basic idea of the above procedure is to hold back a small amount of data (e.g., one pretreatment period of the treatment group) and use the rest of data to predict the held-back information. The algorithm then chooses the model that on average makes the most accurate predictions. A TSCS dataset with a DID data structure allows us to do so because (1) there exists a set of control units that are never exposed to the treatment and therefore can serve as the basis for estimating time-varying factors and (2) the pretreatment periods of treated units constitute a natural validation set for candidate models. This procedure is computationally inexpensive because with each
![]() $r$
, the IFE model is estimated only once (Step 1). Other steps involves merely simple calculations. In the Online Appendix, we conduct Monte Carlo exercises and show that the above procedure performs well in term of choosing the correct number of factors even with relatively small datasets.
$r$
, the IFE model is estimated only once (Step 1). Other steps involves merely simple calculations. In the Online Appendix, we conduct Monte Carlo exercises and show that the above procedure performs well in term of choosing the correct number of factors even with relatively small datasets.
Remark 3. Our framework can also accommodate DGPs that directly incorporate additive fixed effects, known time trends, and exogenous time-invariant covariates, such as:
in which
![]() $l_{t}$
is a
$l_{t}$
is a
![]() $(q\times 1)$
vector of known time trends that may affect each unit differently;
$(q\times 1)$
vector of known time trends that may affect each unit differently;
![]() $\unicode[STIX]{x1D6FE}_{i}$
is
$\unicode[STIX]{x1D6FE}_{i}$
is
![]() $(q\times 1)$
unit-specific unknown parameters;
$(q\times 1)$
unit-specific unknown parameters;
![]() $z_{i}$
is a
$z_{i}$
is a
![]() $(m\times 1)$
vector of observed time-invariant covariates;
$(m\times 1)$
vector of observed time-invariant covariates;
![]() $\unicode[STIX]{x1D703}_{t}$
is a
$\unicode[STIX]{x1D703}_{t}$
is a
![]() $(m\times 1)$
vector of unknown parameters;
$(m\times 1)$
vector of unknown parameters;
![]() $\unicode[STIX]{x1D6FC}_{i}$
and
$\unicode[STIX]{x1D6FC}_{i}$
and
![]() $\unicode[STIX]{x1D709}_{t}$
are additive individual and time fixed effects, respectively. We describe the estimation procedure of this extended model in the Online Appendix.
$\unicode[STIX]{x1D709}_{t}$
are additive individual and time fixed effects, respectively. We describe the estimation procedure of this extended model in the Online Appendix.
3.2 Inference
We rely on a parametric bootstrap procedure to obtain the uncertainty estimates of the GSC estimator (deriving the analytical asymptotic distribution of the GSC estimator is a necessary step for future research). When the sample size is large, when
![]() $N_{tr}$
is large in particular, a simple nonparametric bootstrap procedure can provide valid uncertainty estimates. When the sample size is small, especially when
$N_{tr}$
is large in particular, a simple nonparametric bootstrap procedure can provide valid uncertainty estimates. When the sample size is small, especially when
![]() $N_{tr}$
is small, we are unable to approximate the DGP of the treatment group by resampling the data nonparametrically. In this case, we simply lack the information of the joint distribution of
$N_{tr}$
is small, we are unable to approximate the DGP of the treatment group by resampling the data nonparametrically. In this case, we simply lack the information of the joint distribution of
![]() $(X_{i},\unicode[STIX]{x1D706}_{i},\unicode[STIX]{x1D6FF}_{i})$
for the treatment group. However, we can obtain uncertainty estimates conditional on observed covariates and unobserved factors and factor loadings using a parametric bootstrap procedure via resampling the residuals. By resampling entire time series of residuals, we preserve the serial correlation within the units, thus avoiding underestimating the standard errors due to serial correlations (Beck and Katz Reference Beck and Katz1995). Our goal is to estimate the conditional variance of ATT estimator, i.e.,
$(X_{i},\unicode[STIX]{x1D706}_{i},\unicode[STIX]{x1D6FF}_{i})$
for the treatment group. However, we can obtain uncertainty estimates conditional on observed covariates and unobserved factors and factor loadings using a parametric bootstrap procedure via resampling the residuals. By resampling entire time series of residuals, we preserve the serial correlation within the units, thus avoiding underestimating the standard errors due to serial correlations (Beck and Katz Reference Beck and Katz1995). Our goal is to estimate the conditional variance of ATT estimator, i.e.,
![]() $\text{Var}_{\unicode[STIX]{x1D700}}(\widehat{ATT}_{t}|D,X,\unicode[STIX]{x1D6EC},F)$
. Notice that the only random variable that is not being conditioned on is
$\text{Var}_{\unicode[STIX]{x1D700}}(\widehat{ATT}_{t}|D,X,\unicode[STIX]{x1D6EC},F)$
. Notice that the only random variable that is not being conditioned on is
![]() $\unicode[STIX]{x1D700}_{i}$
, which are assumed to be independent of treatment assignment, observed covariates, factors and factor loadings (Assumption 2). We can interpret
$\unicode[STIX]{x1D700}_{i}$
, which are assumed to be independent of treatment assignment, observed covariates, factors and factor loadings (Assumption 2). We can interpret
![]() $\unicode[STIX]{x1D700}_{i}$
as measurement errors or variations in the outcome that we cannot explain but are unrelated to treatment assignment.Footnote
16
$\unicode[STIX]{x1D700}_{i}$
as measurement errors or variations in the outcome that we cannot explain but are unrelated to treatment assignment.Footnote
16
In the parametric bootstrap procedure, we simulate treated counterfactuals and control units based on the following resampling scheme:
in which
![]() ${\tilde{Y}}_{i}(0)$
is a vector of simulated outcomes in the absence of the treatment;
${\tilde{Y}}_{i}(0)$
is a vector of simulated outcomes in the absence of the treatment;
![]() $X_{i}\hat{\unicode[STIX]{x1D6FD}}+\hat{F}\hat{\unicode[STIX]{x1D706}}_{i}$
is the estimated conditional mean; and
$X_{i}\hat{\unicode[STIX]{x1D6FD}}+\hat{F}\hat{\unicode[STIX]{x1D706}}_{i}$
is the estimated conditional mean; and
![]() $\tilde{\unicode[STIX]{x1D700}}_{i}$
and
$\tilde{\unicode[STIX]{x1D700}}_{i}$
and
![]() $\tilde{\unicode[STIX]{x1D700}}_{i}^{p}$
are resampled residuals for unit
$\tilde{\unicode[STIX]{x1D700}}_{i}^{p}$
are resampled residuals for unit
![]() $i$
, depending on whether it belongs to the treatment or control group. Because
$i$
, depending on whether it belongs to the treatment or control group. Because
![]() $\hat{\unicode[STIX]{x1D6FD}}$
are
$\hat{\unicode[STIX]{x1D6FD}}$
are
![]() $\hat{F}$
are estimated using only the control group information,
$\hat{F}$
are estimated using only the control group information,
![]() $X_{i}\hat{\unicode[STIX]{x1D6FD}}+\hat{F}\hat{\unicode[STIX]{x1D706}}_{i}$
fits
$X_{i}\hat{\unicode[STIX]{x1D6FD}}+\hat{F}\hat{\unicode[STIX]{x1D706}}_{i}$
fits
![]() $X_{i}\unicode[STIX]{x1D6FD}+F\unicode[STIX]{x1D706}_{i}$
better for a control unit than for a treated unit (as a result, the variance of
$X_{i}\unicode[STIX]{x1D6FD}+F\unicode[STIX]{x1D706}_{i}$
better for a control unit than for a treated unit (as a result, the variance of
![]() $\tilde{\unicode[STIX]{x1D700}}_{i}^{p}$
is usually bigger than that of
$\tilde{\unicode[STIX]{x1D700}}_{i}^{p}$
is usually bigger than that of
![]() $\tilde{\unicode[STIX]{x1D700}}_{i}$
). Hence,
$\tilde{\unicode[STIX]{x1D700}}_{i}$
). Hence,
![]() $\tilde{\unicode[STIX]{x1D700}}_{i}$
and
$\tilde{\unicode[STIX]{x1D700}}_{i}$
and
![]() $\tilde{\unicode[STIX]{x1D700}}_{i}^{p}$
are drawn from different empirical distributions:
$\tilde{\unicode[STIX]{x1D700}}_{i}^{p}$
are drawn from different empirical distributions:
![]() $\tilde{\unicode[STIX]{x1D700}}_{i}$
is the in-sample error of the IFE model fitted to the control group data, and therefore is drawn from the empirical distribution of the residuals of the IFE model, while
$\tilde{\unicode[STIX]{x1D700}}_{i}$
is the in-sample error of the IFE model fitted to the control group data, and therefore is drawn from the empirical distribution of the residuals of the IFE model, while
![]() $\tilde{\unicode[STIX]{x1D700}}_{i}^{p}$
can be seen as the prediction error of the IFE model for treated counterfactuals.Footnote
17
$\tilde{\unicode[STIX]{x1D700}}_{i}^{p}$
can be seen as the prediction error of the IFE model for treated counterfactuals.Footnote
17
Although we cannot observe treated counterfactuals,
![]() $Y_{it}(0)$
is observed for all control units. With the assumptions that treated and control units follow the same factor model (Assumption 1) and the error terms are independent and homoscedastic across space (Assumption 5), we can use a cross-validation method to simulate
$Y_{it}(0)$
is observed for all control units. With the assumptions that treated and control units follow the same factor model (Assumption 1) and the error terms are independent and homoscedastic across space (Assumption 5), we can use a cross-validation method to simulate
![]() $\unicode[STIX]{x1D700}_{i}^{p}$
based on the control group data (Efron Reference Efron2012). Specifically, each time we leave one control unit out (to be taken as a “fake” treat unit) and use the rest of the control units to predict the outcome of left-out unit. The difference between the predicted and observed outcomes is a prediction error of the IFE model.
$\unicode[STIX]{x1D700}_{i}^{p}$
based on the control group data (Efron Reference Efron2012). Specifically, each time we leave one control unit out (to be taken as a “fake” treat unit) and use the rest of the control units to predict the outcome of left-out unit. The difference between the predicted and observed outcomes is a prediction error of the IFE model.
![]() $\unicode[STIX]{x1D700}_{i}^{p}$
is drawn from the empirical distributions of the prediction errors. Under Assumptions 1–5, this procedure provides valid uncertainty estimates for the proposed method without making particular distributional assumptions of the error terms. Algorithm 2 describes the entire procedure in detail.
$\unicode[STIX]{x1D700}_{i}^{p}$
is drawn from the empirical distributions of the prediction errors. Under Assumptions 1–5, this procedure provides valid uncertainty estimates for the proposed method without making particular distributional assumptions of the error terms. Algorithm 2 describes the entire procedure in detail.
Algorithm 2 (Inference).
A parametric bootstrap procedure that gives the uncertainty estimates of the ATT is described as follows:

4 Monte Carlo Evidence
In this section, we conduct Monte Carlo exercises to explore the finite sample properties of the GSC estimator and compare it with several existing methods, including the DID estimator, the IFE estimator, and the original synthetic matching method. We also investigate the extent to which the proposed cross-validation scheme can choose the number of factors correctly in relatively small samples.
We start with the following data generating process (DGP) that includes two observed time-varying covariates, two unobserved factors, and additive two-way fixed effects:
where
![]() $f_{t}=(f_{1t},f_{2t})^{\prime }$
and
$f_{t}=(f_{1t},f_{2t})^{\prime }$
and
![]() $\unicode[STIX]{x1D706}_{i}=(\unicode[STIX]{x1D706}_{i1},\unicode[STIX]{x1D706}_{i2})^{\prime }$
are time-varying factors and unit-specific factor loadings. The covariates are (positively) correlated with both the factors and factor loadings:
$\unicode[STIX]{x1D706}_{i}=(\unicode[STIX]{x1D706}_{i1},\unicode[STIX]{x1D706}_{i2})^{\prime }$
are time-varying factors and unit-specific factor loadings. The covariates are (positively) correlated with both the factors and factor loadings:
![]() $x_{it,k}=1+\unicode[STIX]{x1D706}_{i}^{\prime }f_{t}+\unicode[STIX]{x1D706}_{i1}+\unicode[STIX]{x1D706}_{i2}+f_{1t}+f_{2t}+\unicode[STIX]{x1D702}_{it,k},k=1,2$
. The error term
$x_{it,k}=1+\unicode[STIX]{x1D706}_{i}^{\prime }f_{t}+\unicode[STIX]{x1D706}_{i1}+\unicode[STIX]{x1D706}_{i2}+f_{1t}+f_{2t}+\unicode[STIX]{x1D702}_{it,k},k=1,2$
. The error term
![]() $\unicode[STIX]{x1D700}_{it}$
and disturbances in covariates
$\unicode[STIX]{x1D700}_{it}$
and disturbances in covariates
![]() $\unicode[STIX]{x1D702}_{it,1}$
and
$\unicode[STIX]{x1D702}_{it,1}$
and
![]() $\unicode[STIX]{x1D702}_{it,2}$
are i.i.d.
$\unicode[STIX]{x1D702}_{it,2}$
are i.i.d.
![]() $N(0,1)$
. Factors
$N(0,1)$
. Factors
![]() $f_{1t}$
and
$f_{1t}$
and
![]() $f_{2t}$
, as well as time fixed effects
$f_{2t}$
, as well as time fixed effects
![]() $\unicode[STIX]{x1D709}_{t}$
, are also i.i.d.
$\unicode[STIX]{x1D709}_{t}$
, are also i.i.d.
![]() $N(0,1)$
. The treatment and control groups consist of
$N(0,1)$
. The treatment and control groups consist of
![]() $N_{tr}$
and
$N_{tr}$
and
![]() $N_{co}$
units. The treatment starts to affect the treated units at time
$N_{co}$
units. The treatment starts to affect the treated units at time
![]() $T_{0}+1$
and since then 10 periods are observed (
$T_{0}+1$
and since then 10 periods are observed (
![]() $q=10$
). The treatment indicator is defined as in Section 2, i.e.,
$q=10$
). The treatment indicator is defined as in Section 2, i.e.,
![]() $D_{it}=1$
when
$D_{it}=1$
when
![]() $i\in {\mathcal{T}}$
and
$i\in {\mathcal{T}}$
and
![]() $t>T_{0}$
and
$t>T_{0}$
and
![]() $D_{it}=0$
otherwise. The heterogeneous treatment effect is generated by
$D_{it}=0$
otherwise. The heterogeneous treatment effect is generated by
![]() $\unicode[STIX]{x1D6FF}_{it,t>T_{0}}=\bar{\unicode[STIX]{x1D6FF}}_{t}+e_{it}$
, in which
$\unicode[STIX]{x1D6FF}_{it,t>T_{0}}=\bar{\unicode[STIX]{x1D6FF}}_{t}+e_{it}$
, in which
![]() $e_{it}$
is i.i.d. N(0,1).
$e_{it}$
is i.i.d. N(0,1).
![]() $\bar{\unicode[STIX]{x1D6FF}}_{t}$
is given by:
$\bar{\unicode[STIX]{x1D6FF}}_{t}$
is given by:
![]() $[\bar{\unicode[STIX]{x1D6FF}}_{T_{0}+1},\bar{\unicode[STIX]{x1D6FF}}_{T_{0}+1},\ldots ,\bar{\unicode[STIX]{x1D6FF}}_{T_{0}+10}]=[1,2,\ldots ,10]$
.
$[\bar{\unicode[STIX]{x1D6FF}}_{T_{0}+1},\bar{\unicode[STIX]{x1D6FF}}_{T_{0}+1},\ldots ,\bar{\unicode[STIX]{x1D6FF}}_{T_{0}+10}]=[1,2,\ldots ,10]$
.
Factor loadings
![]() $\unicode[STIX]{x1D706}_{i1}$
and
$\unicode[STIX]{x1D706}_{i1}$
and
![]() $\unicode[STIX]{x1D706}_{i2}$
, as well as unit fixed effects
$\unicode[STIX]{x1D706}_{i2}$
, as well as unit fixed effects
![]() $\unicode[STIX]{x1D6FC}_{i}$
, are drawn from uniform distributions
$\unicode[STIX]{x1D6FC}_{i}$
, are drawn from uniform distributions
![]() $U[-\sqrt{3},\sqrt{3}]$
for control units and
$U[-\sqrt{3},\sqrt{3}]$
for control units and
![]() $U[\sqrt{3}-2w\sqrt{3},3\sqrt{3}-2w\sqrt{3}]$
for treated units (
$U[\sqrt{3}-2w\sqrt{3},3\sqrt{3}-2w\sqrt{3}]$
for treated units (
![]() $w\in [0,1]$
). This means that when
$w\in [0,1]$
). This means that when
![]() $0\leqslant w<1$
, (1) the random variables have variance 1; (2) the supports of factor loadings of treated and control units are not perfectly overlapped; and (3) the treatment indicator and factor loadings are positively correlated.Footnote
18
$0\leqslant w<1$
, (1) the random variables have variance 1; (2) the supports of factor loadings of treated and control units are not perfectly overlapped; and (3) the treatment indicator and factor loadings are positively correlated.Footnote
18
4.1 A simulated example
We first illustrate the proposed method, as well as the DGP described above, with a simulated sample of
![]() $N_{tr}=5$
,
$N_{tr}=5$
,
![]() $N_{co}=45$
, and
$N_{co}=45$
, and
![]() $T_{0}=20$
(hence,
$T_{0}=20$
(hence,
![]() $N=50$
,
$N=50$
,
![]() $T=30$
).
$T=30$
).
![]() $w$
is set to be
$w$
is set to be
![]() $0.8$
, which means that the treated units are more likely to have larger factor loadings than the control units. Figure 1 visualizes the raw data and estimation results. In the upper panel, the dark and light gray lines are time series of the treated and control units, respectively. The bold solid line is the average outcome of the five treated units while the bold dashed line is the average predicted outcome of the five units in the absence of the treatment. The latter is imputed using the proposed method.
$0.8$
, which means that the treated units are more likely to have larger factor loadings than the control units. Figure 1 visualizes the raw data and estimation results. In the upper panel, the dark and light gray lines are time series of the treated and control units, respectively. The bold solid line is the average outcome of the five treated units while the bold dashed line is the average predicted outcome of the five units in the absence of the treatment. The latter is imputed using the proposed method.
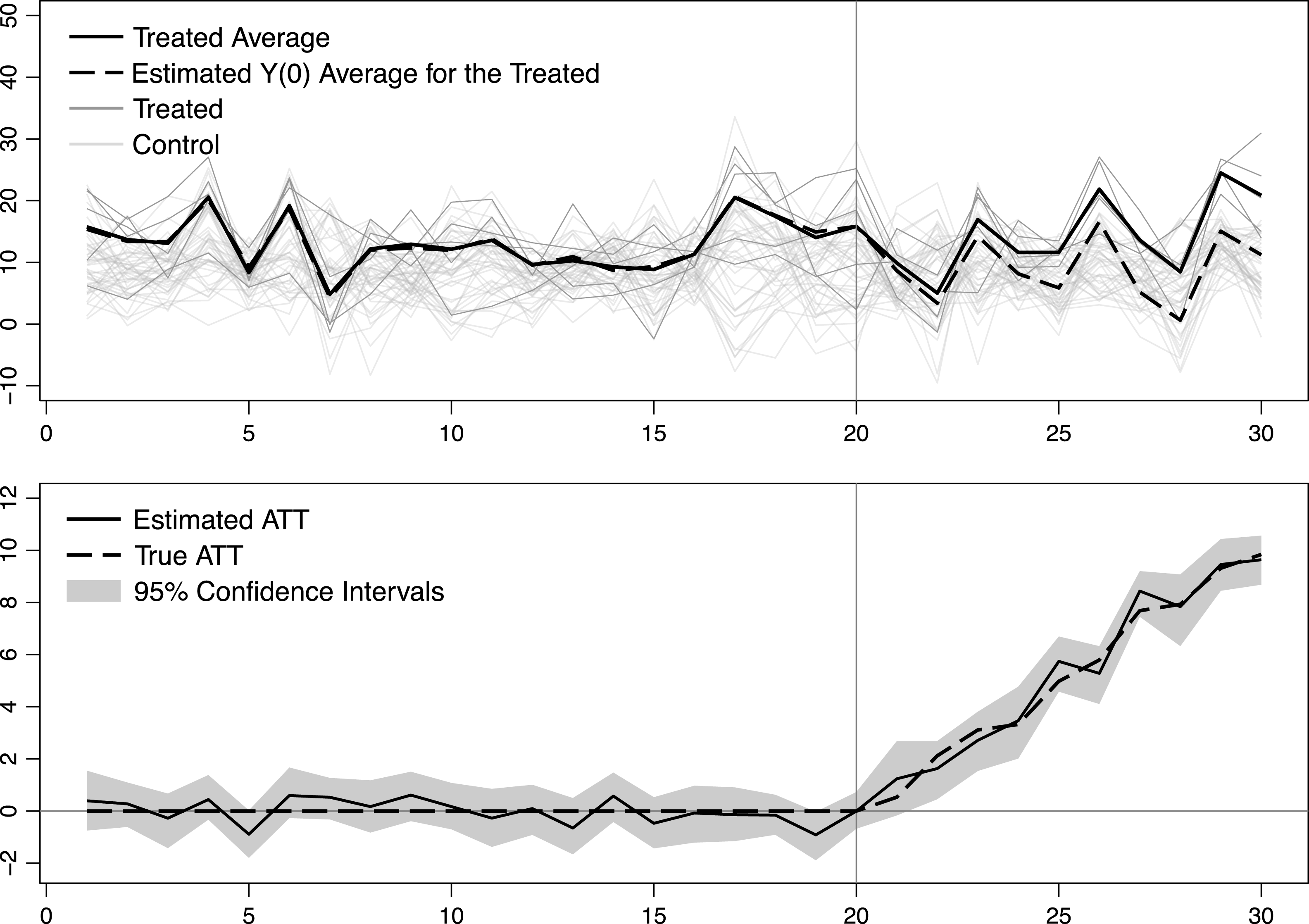
Figure 1. Estimated ATT for a simulated sample
![]() $N_{tr}=5$
,
$N_{tr}=5$
,
![]() $N_{co}=45$
,
$N_{co}=45$
,
![]() $T=30$
,
$T=30$
,
![]() $T_{0}=10$
.
$T_{0}=10$
.
The lower panel of Figure 1 shows the estimated ATT (solid line) and the true ATT (dashed line). The 95 percent confidence intervals for the ATT are based on bootstraps of 2,000 times. It shows that the estimated average treated outcome fits the data well in pretreatment periods and the estimated ATT is very close to the actual ATT. The estimated factors and factor loadings, as well as imputed counterfactual and individual treatment effect for each treat unit, are shown in the Online Appendix.
4.2 Finite sample properties
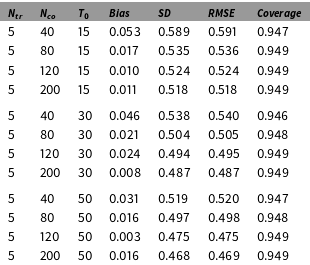
We present the Monte Carlo evidence on the finite sample properties of the GSC estimator in Table 1 (additional results are shown in the Online Appendix). As in the previous example, the treatment group is set to have five units. The estimand is the ATT at time
![]() $T_{0}+5$
, whose expected value equals 5. Observables, factors, and factor loadings are drawn only once while the error term is drawn repeatedly;
$T_{0}+5$
, whose expected value equals 5. Observables, factors, and factor loadings are drawn only once while the error term is drawn repeatedly;
![]() $w$
is set to be 0.8 such that treatment assignment is positively correlated with factor loadings. Table 1 reports the bias, standard deviation (SD), and root mean squared error (RMSE) of
$w$
is set to be 0.8 such that treatment assignment is positively correlated with factor loadings. Table 1 reports the bias, standard deviation (SD), and root mean squared error (RMSE) of
![]() $\widehat{ATT}_{T_{0}+5}$
from 5,000 simulations for each pair of
$\widehat{ATT}_{T_{0}+5}$
from 5,000 simulations for each pair of
![]() $T_{0}$
and
$T_{0}$
and
![]() $N_{co}$
.Footnote
19
It shows that the GSC estimator has limited bias even when
$N_{co}$
.Footnote
19
It shows that the GSC estimator has limited bias even when
![]() $T_{0}$
and
$T_{0}$
and
![]() $N_{co}$
are relatively small and the bias goes away as
$N_{co}$
are relatively small and the bias goes away as
![]() $T_{0}$
and
$T_{0}$
and
![]() $N_{co}$
grow. As expected, both the SD and RMSE shrink when
$N_{co}$
grow. As expected, both the SD and RMSE shrink when
![]() $T_{0}$
and
$T_{0}$
and
![]() $N_{co}$
become larger. Table 1 also reports the coverage probabilities of 95 percent confidence intervals for
$N_{co}$
become larger. Table 1 also reports the coverage probabilities of 95 percent confidence intervals for
![]() $\widehat{ATT}_{i,T_{0}+5}$
constructed by the parametric bootstrap procedure (Algorithm 2). For each pair of
$\widehat{ATT}_{i,T_{0}+5}$
constructed by the parametric bootstrap procedure (Algorithm 2). For each pair of
![]() $T_{0}$
and
$T_{0}$
and
![]() $N_{co}$
, the coverage probability is calculated based on 5,000 simulated samples, each of which is bootstrapped for 1,000 times. These numbers show that the proposed procedure can achieve the correct coverage rate even when the sample size is relatively small (e.g.,
$N_{co}$
, the coverage probability is calculated based on 5,000 simulated samples, each of which is bootstrapped for 1,000 times. These numbers show that the proposed procedure can achieve the correct coverage rate even when the sample size is relatively small (e.g.,
![]() $T_{0}=15$
,
$T_{0}=15$
,
![]() $N_{tr}=5$
,
$N_{tr}=5$
,
![]() $N_{co}=80$
).
$N_{co}=80$
).
Table 1. Finite sample properties and coverage rates
In the Online Appendix, we run additional simulations and compare the proposed method with several existing methods, including the DID estimator, the IFE estimator, and the synthetic matching method. We find that (1) the GSC estimator has less bias than the DID estimator in the presence of unobserved, decomposable time-varying confounders; (2) it has less bias than the IFE estimator when the treatment effect is heterogeneous; and (3) it is usually more efficient than the original synthetic matching estimator. It is worth emphasizing that these results are under the premise of correct model specifications. To address the concern that the GSC method relies on correct model specifications, we conduct additional tests and show that the cross-validation scheme described in Algorithm 1 is able to choose the number of factors correctly most of the time when the sample is large enough.
5 Empirical Example
In this section, we illustrate the GSC method with an empirical example that investigates the effect of EDR laws on voter turnout in the United States. Voting in the United States usually takes two steps. Except in North Dakota, where no registration is needed, eligible voters throughout the country must register prior to casting their ballots. Registration, which often requires a separate trip from voting, is widely regarded as a substantial cost of voting and a culprit of low turnout rates before the 1993 National Voter Registration Act (NVRA) was enacted (e.g., Highton Reference Highton2004). Against this backdrop, EDR is a reform that allows eligible voters to register on Election Day when they arrive at polling stations. In the mid-1970s, Maine, Minnesota, and Wisconsin were the first adopters of this reform in the hopes of increasing voter turnout; while Idaho, New Hampshire, and Wyoming established EDR in the 1990s as a strategy to opt out the NVRA (Hanmer Reference Hanmer2009). Before the 2012 presidential election, three other states, Montana, Iowa, and Connecticut, passed laws to enact EDR, adding the number of states having EDR laws to nine.Footnote 20
Most existing studies based on individual-level cross-sectional data, such as the Current Population Surveys and the National Election Surveys, suggest that EDR laws increase turnout (the estimated effect varies from 5 to 14 percentage points).Footnote 21 These studies do not provide compelling evidence of a causal effect of EDR laws because the research designs they use are insufficient to address the problem that states self-select their systems of registration laws. “Registration requirements did not descend from the skies,” as Dean Burnham puts it (Reference Burnham and Rose1980, p. 69). A few studies employ time-series or TSCS analysis to address the identification problem.Footnote 22 However, Keele and Minozzi (Reference Keele and Minozzi2013) cast doubts on these studies and suggest that the “parallel trends” assumption may not hold, as we will also demonstrate below.
In the following analysis, we use state-level voter turnout data for presidential elections from 1920 to 2012.Footnote 23 The turnout rates are calculated with total ballots counted in a presidential election in a state as the numerator and the state’s voting-age population (VAP) as the denominator.Footnote 24 Alaska and Hawaii are not included in the sample since they were not states until 1959. North Dakota is also dropped since no registration is required. As mentioned above, up to the 2012 presidential election, nine states had adopted EDR laws (hereafter referred to as treated) and the rest thirty-eight states had not (referred to as controls). The raw turnout data for all forty-seven states are shown in the Online Appendix.Footnote 25
First, we use a standard two-way fixed effects mode, which is often referred to as a DID model in the literature. The results are shown in Table 2 columns (1) and (2). Standard errors are produced by nonparametric bootstraps (blocked at the state level) of 2,000 times. In column (1), only the EDR indicator is included, while in column (2), we additionally control for indicators of universal mail-in registration and motor voter registration. The estimated coefficients of EDR laws are 0.87 and 0.78 percent using the two specifications, respectively, with standard errors around 3 percent.
Table 2. The effect of EDR on voter turnout
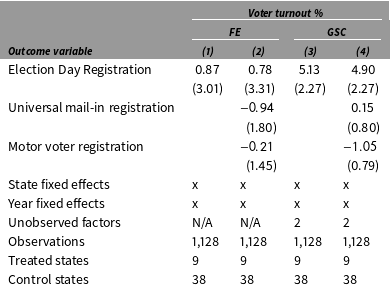
Note: Standard errors in columns (1) and (2) are based on nonparametric bootstraps (blocked at the state level) of 2,000 times. Standard errors in columns (3) and (4) are based on parametric bootstraps (blocked at the state level) of 2,000 times.
The two-way fixed effects model presented in Table 2 assumes a constant treatment effect both across states and over time. Next we relax this assumption by literally employing a DID approach. In other words, we estimate the effect of EDR laws on voter turnout in the posttreatment period by subtracting the time intercepts estimated from the control group and the unit intercepts based on the pretreatment data. The predict turnout for state
![]() $i$
in year
$i$
in year
![]() $t$
, therefore, is the summation of unit intercept
$t$
, therefore, is the summation of unit intercept
![]() $i$
and time intercept
$i$
and time intercept
![]() $t$
, plus the impact of the time-varying covariates. The result is visualized in the upper panel of Figure 2. Figure 2a shows the average actual turnout (solid line) and average predicted turnout in the absence of EDR laws (dashed line); both averages are taken based on the number of terms since (or before) EDR laws first took effect. Figure 2b shows the gap between the two lines, or the estimated ATT. The confidence intervals are produced by block bootstraps of 2,000 times. It is clear from both figures that the “parallel trends” assumption is not likely to hold since the average predicted turnout deviates from the average actual turnout in the pretreatment periods.
$t$
, plus the impact of the time-varying covariates. The result is visualized in the upper panel of Figure 2. Figure 2a shows the average actual turnout (solid line) and average predicted turnout in the absence of EDR laws (dashed line); both averages are taken based on the number of terms since (or before) EDR laws first took effect. Figure 2b shows the gap between the two lines, or the estimated ATT. The confidence intervals are produced by block bootstraps of 2,000 times. It is clear from both figures that the “parallel trends” assumption is not likely to hold since the average predicted turnout deviates from the average actual turnout in the pretreatment periods.
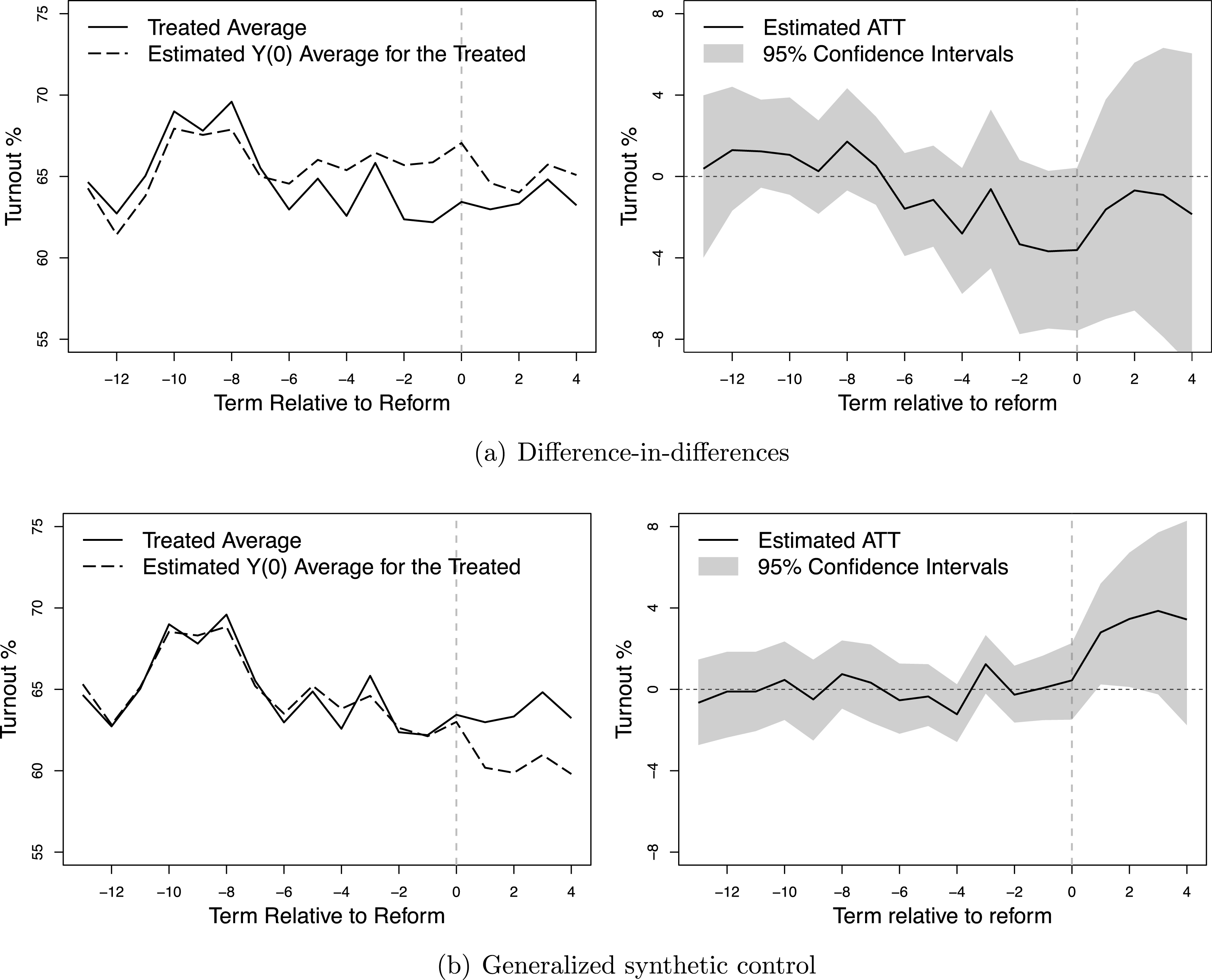
Figure 2. The effect of EDR on turnout: Main results.
Next, we apply the GSC method to the same dataset. Table 2 columns (3) and (4) summarize the result.Footnote 26 Again, both specifications impose additive state and year fixed effects. In column (3), no covariates are included, while in column (4), mail-in and motor voter registration are controlled for (assuming that they have constant effects on turnout). With both specifications, the cross-validation scheme finds two unobserved factors to be important and after conditioning on both the factors and additive fixed effects, the estimated ATT based on the GSC method is around 5 percent with a standard error of 2.3 percent.Footnote 27 This means that EDR laws are associated with a statistically significant increase in voter turnout, consistent with previous OLS results based on individual-level data. The lower panel of Figure 2 shows the dynamics of the estimated ATT. Again, in the left figure, averages are taken after the actual and predicted turnout rates are realigned to the timing of the reform. With the GSC method, the average actual turnout and average predicted turnout match well in pretreatment periods and diverge after EDR laws took effect. The right figure shows that the gaps between the two lines are virtually flat in pretreatment periods and the effect takes off right after the adoption of EDR.Footnote 28
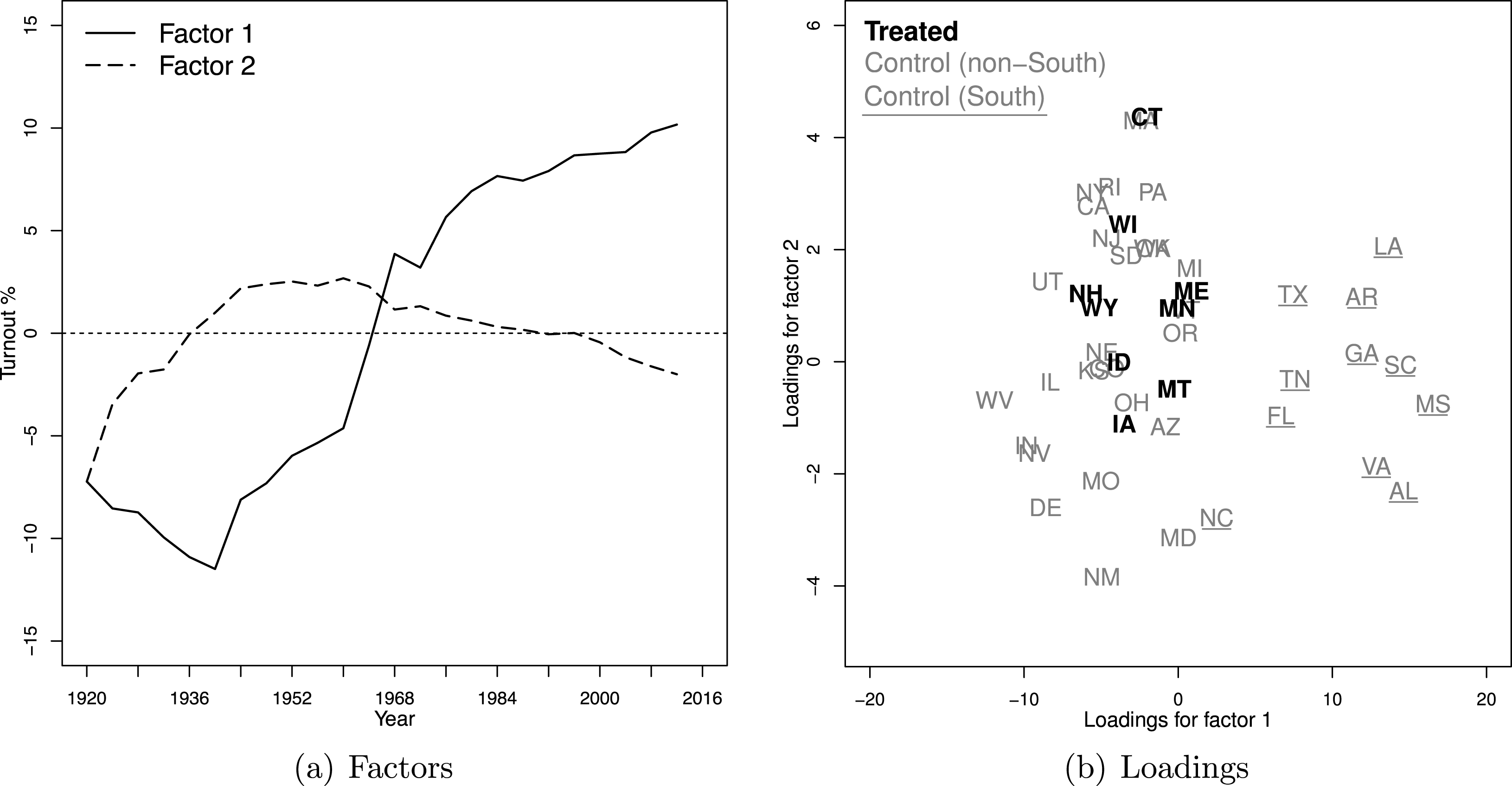
Figure 3. The Effect of EDR on turnout: Factors and loadings.
Figure 3 presents the estimated factors and factor loadings produced by the GSC method.Footnote
29
Figure 3a depicts the two estimated factors. The
![]() $x$
-axis is year and the
$x$
-axis is year and the
![]() $y$
-axis is the magnitude of factors (rescaled by the square root of their corresponding eigenvalues to demonstrate their relative importance). Figure 3b shows the estimated factors loadings for each treated (black, bold) and control (gray) units, with
$y$
-axis is the magnitude of factors (rescaled by the square root of their corresponding eigenvalues to demonstrate their relative importance). Figure 3b shows the estimated factors loadings for each treated (black, bold) and control (gray) units, with
![]() $x$
- and
$x$
- and
![]() $y$
-axes indicating the magnitude of the loadings for the first and second factors, respectively. Bearing in mind the caveat that estimated factors may not be directly interpretable because they are, at best, linear transformations of the true factors, we find that the estimated factors shown in this figure are meaningful. The first factor captures the sharp increase in turnout in the southern states because of the 1965 Voting Rights Act that removed Jim Crow laws, such as poll taxes or literacy tests, that suppressed turnout. As shown in the right figure, the top eleven states that have the largest loadings on the first factor are exactly the eleven southern states (which were previously in the confederacy).Footnote
30
The labels of these states are underlined in Figure 3b. The second factor, which is set to be orthogonal to the first one, is less interpretable. However, its nonnegligible magnitude indicates a strong downward trend in voter turnout in many states in recent years. Another reassuring finding shown by Figure 3b is that the estimated factor loadings of the nine treated units mostly lie in the convex hull of those of the control units, which indicates that the treated counterfactuals are produced mostly by more reliable interpolations instead of extrapolations.
$y$
-axes indicating the magnitude of the loadings for the first and second factors, respectively. Bearing in mind the caveat that estimated factors may not be directly interpretable because they are, at best, linear transformations of the true factors, we find that the estimated factors shown in this figure are meaningful. The first factor captures the sharp increase in turnout in the southern states because of the 1965 Voting Rights Act that removed Jim Crow laws, such as poll taxes or literacy tests, that suppressed turnout. As shown in the right figure, the top eleven states that have the largest loadings on the first factor are exactly the eleven southern states (which were previously in the confederacy).Footnote
30
The labels of these states are underlined in Figure 3b. The second factor, which is set to be orthogonal to the first one, is less interpretable. However, its nonnegligible magnitude indicates a strong downward trend in voter turnout in many states in recent years. Another reassuring finding shown by Figure 3b is that the estimated factor loadings of the nine treated units mostly lie in the convex hull of those of the control units, which indicates that the treated counterfactuals are produced mostly by more reliable interpolations instead of extrapolations.
Finally, we investigate the heterogeneous treatment effects of EDR laws. Previous studies have suggested that the motivations behind enacting these laws are vastly different between the early adopters and later ones. For example, Maine, Minnesota, and Wisconsin, which established the EDR in mid-1970s, did so because officials in these states sincerely wanted the turnout rates to be higher, while the “reluctant adopters,” including Idaho, New Hampshire, and Wyoming, introduced the EDR as a means to avoid the NVRA because officials viewed the NVRA as “a more costly and potentially chaotic system” (Hanmer Reference Hanmer2009). Because of the different motivations and other reasons, we may expect the treatment effect of EDR laws to be different in states that adopted them in different times.
Table 3. The effect of EDR on voter turnout: Three waves
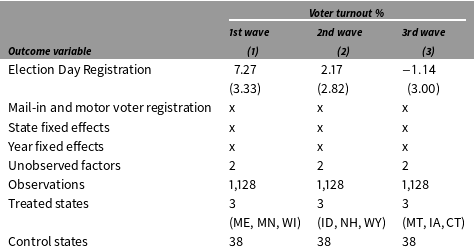
Note: Standard errors are based on parametric bootstraps (blocked at the state level) of 1,000 times.
The estimation of heterogeneous treatment effects is embedded in the GSC method since it gives individual treatment effects for all treated units in a single run. Table 3 summarizes the ATTs of EDR on voter turnout among the three waves of EDR adopters. Again, additive state and year fixed effects, as well as indicators of two other registration systems, are controlled for. Table 3 shows that EDR laws have a large and positive effect on the early adopters (the estimate is about 7 percent with a standard error of 3 percent) while EDR laws were found to have no statistically significant impact on the other six states.Footnote 31 Such differential outcomes can be due to two reasons. First, the NVRA of 1993 substantially reduced the cost of registration: since almost everyone who has some intention to vote is a registrant after the NVRA was enacted, “there is now little room for enhancing turnout further by making registration easier” (Highton Reference Highton2004). Second, because states having a strong “participatory culture” is more likely to be selected into an EDR system in earlier years, costly registration, as a binding constraint in these states, may not be a first-order issue in a state where many eligible voters have low incentives to vote in the first place. It is also possible that voters in early adopting states formed a habit to vote in the days when the demand for participation was high (Hanmer Reference Hanmer2009).
In short, using the GSC method, we find that EDR laws increased turnout in early adopting states, including Maine, Minnesota, and Wisconsin, but not in states that introduced EDR as a strategy to opt out the NVRA or enacted EDR laws in recent years. These results are broadly consistent with evidence provided by a large literature based on individual-level cross-sectional data (see, for example, Leighley and Nagler Reference Leighley and Nagler2013 for a summary). They are also more credible than results from conventional fixed effects models when the “parallel trends” assumption appears to fail.Footnote 32
6 Conclusion
In this paper, we propose the GSC method for causal inference with TSCS data. It attempts to address the challenge that the “parallel trends” assumption often fails when researchers apply fixed effects models to estimate the causal effect of a certain treatment. The GSC method estimates the individual treatment effect on each treated unit semiparametrically. Specifically, it imputes treated counterfactuals based on a linear interactive fixed effects model that incorporates time-varying coefficients (factors) interacted with unit-specific intercepts (factor loadings). A built-in cross-validation scheme automatically selects the model, reducing the risks of overfitting.
This method is in spirit of the original synthetic control method in that it uses data from pretreatment periods as benchmarks to customize a reweighting scheme of control units in order to make the best possible predictions for treated counterfactuals. It generalizes the synthetic control method in two aspects. First, it allows multiple treated units and differential treatment timing. Second, it offers uncertainty estimates, such as standard errors and confidence intervals, that are easy to interpret.
Monte Carlo exercises suggest that the proposed method performs well even with relatively small
![]() $T_{0}$
and
$T_{0}$
and
![]() $N_{co}$
and show that it has advantages over several existing methods: (1) it has less bias than the two-way fixed effects or DID estimators in the presence of decomposable time-varying confounders, (2) it corrects bias of the IFE estimator when the treatment effect is heterogeneous across units; and (3) it is more efficient than the synthetic control method. To illustrate the applicability of this method in political science, we estimate the effect of EDR laws on voter turnout in the United States. We show that EDR laws increased turnout in early adopting states but not in states that introduced them more recently.
$N_{co}$
and show that it has advantages over several existing methods: (1) it has less bias than the two-way fixed effects or DID estimators in the presence of decomposable time-varying confounders, (2) it corrects bias of the IFE estimator when the treatment effect is heterogeneous across units; and (3) it is more efficient than the synthetic control method. To illustrate the applicability of this method in political science, we estimate the effect of EDR laws on voter turnout in the United States. We show that EDR laws increased turnout in early adopting states but not in states that introduced them more recently.
Two caveats are worth emphasizing. First, insufficient data (with either a small
![]() $T_{0}$
or a small
$T_{0}$
or a small
![]() $N_{co}$
) cause bias in the estimated treatment effect. In general, users should be cautious when
$N_{co}$
) cause bias in the estimated treatment effect. In general, users should be cautious when
![]() $T_{0}<10$
or
$T_{0}<10$
or
![]() $N_{co}<40$
. Second, excessive extrapolations based on imprecisely estimated factors and factor loading can lead to erroneous results. To avoid this problem, we recommend the following diagnostics upon using this method: (1) plot raw data of treated and control outcomes as well as imputed counterfactuals and check whether the imputed values are within reasonable intervals; (2) plot estimated factor loadings of both treated and control units and check the overlap (as in Fig. 3). We provide software routines gsynth in R to implement the estimation procedure as well as these diagnostic tests. When excessive extrapolations appear to happen, we recommend users to include a smaller number of factors or switch back to the conventional DID framework. We also recommend users to benchmark the results with estimates from the IFE model (Bai Reference Bai2009) as well as Bayesian multi-level factor models (e.g., Pang Reference Pang2014) whenever it is possible.
$N_{co}<40$
. Second, excessive extrapolations based on imprecisely estimated factors and factor loading can lead to erroneous results. To avoid this problem, we recommend the following diagnostics upon using this method: (1) plot raw data of treated and control outcomes as well as imputed counterfactuals and check whether the imputed values are within reasonable intervals; (2) plot estimated factor loadings of both treated and control units and check the overlap (as in Fig. 3). We provide software routines gsynth in R to implement the estimation procedure as well as these diagnostic tests. When excessive extrapolations appear to happen, we recommend users to include a smaller number of factors or switch back to the conventional DID framework. We also recommend users to benchmark the results with estimates from the IFE model (Bai Reference Bai2009) as well as Bayesian multi-level factor models (e.g., Pang Reference Pang2014) whenever it is possible.
Another limitation of the proposed method is that it cannot accommodate complex DGPs that often appear in TSCS data (when
![]() $T$
is much bigger than panel data), such as (1) dynamic relationships between the treatment, covariates, and outcome (e.g., Pang Reference Pang2010, Reference Pang2014, Blackwell and Glynn Reference Blackwell and Glynn2015), (2) structural breaks (e.g., Park Reference Park2010, Reference Park2012), and (3) multiple times of treatment and variable treatment intensity. Nor does it allow random coefficients for the observed time-varying covariates, as such modeling setups become increasing popular with Bayesian multi-level analysis. Future research is needed to accommodate these scenarios.
$T$
is much bigger than panel data), such as (1) dynamic relationships between the treatment, covariates, and outcome (e.g., Pang Reference Pang2010, Reference Pang2014, Blackwell and Glynn Reference Blackwell and Glynn2015), (2) structural breaks (e.g., Park Reference Park2010, Reference Park2012), and (3) multiple times of treatment and variable treatment intensity. Nor does it allow random coefficients for the observed time-varying covariates, as such modeling setups become increasing popular with Bayesian multi-level analysis. Future research is needed to accommodate these scenarios.
Supplementary material
For supplementary material accompanying this paper, please visit https://doi.org/10.1017/pan.2016.2.








